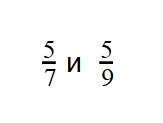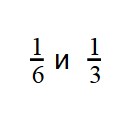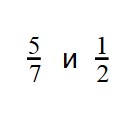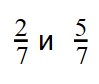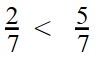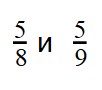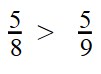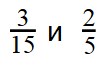какая дробь меньше единицы

Какая дробь меньше единицы?

Ответ прост: правильная дробь меньше единицы. Но что же такое дробь вообще и какова её история?

Сам термин «дробь» происходит от латинского термина «fractura», который является переводом арабского слова «ломать», «раздробить». Таким образом «дробь» — это некое нецелое, дробное число, записанное специальным образом.

Можно сказать, что десятичные дроби впервые стали использовать еще китайцы. По крайней мере, в письменных источниках десятичные дроби упоминаются уже в III веке нашей эры. Хотя, однако, изобретателем десятичных дробей объявлял себя Джамшид Гияс-ад-дин ал-Каши, персидский астроном и математик, живший в XV веке. В Европе обыкновенные дроби и действия с ними стали использоваться уже в XVI веке, а в Древней Руси термин «дробь» впервые упоминается в «Арифметике» Магницкого, датируемой 1703 годом. Однако всё же считается, что основа всей теории обыкновенных дробей была заслугой греческих и индийских математиков.

Математическая дробь — число, которое состоит из одной или нескольких частей (долей) единицы. Дроби делятся на обыкновенные и десятичные по способу записи. Кроме того, дроби могут быть правильными и неправильными. В случае если числитель меньше знаменателя, перед нами правильная дробь. Таким образом, дробь всегда меньше единицы, если она правильная. С другой стороны дробь, у которой числитель меньше знаменателя, всегда меньше единицы и является правильной дробью.

Источник

Какая дробь меньше единицы?

Если речь идёт об обыкновенных дробях, то меньше единицы те дроби, у которых числитель меньше знаменателя, а также все отрицательные дроби.

Если же речь о десятичных дробях, то меньше единицы те дроби, у которых перед знаком десятичного разделителя (запятой или точкой) стоИт исключительно ноль или несколько нулей (за исключением дробей с периодом, равным 9), а также все отрицательные десятичные дроби.

Любая, у которой числитель меньше знаменателя.

Дробь меньше единицы, если числитель меньше знаменателя

Если речь идет о десятичной дроби, то меньше единицы такая дробь, у которой перед запятой стоит ноль. Цифры после запятой значения не имеют. Что касается обыкновенной дроби, то меньше единицы будет та, у которой числитель (верхнее число) меньше, чем знаменатель (нижнее число).

Дробь меньше единицы в том случае, когда числитель (делимое) меньше знаменателя (делителя).

например 1/2, 2/3, 3/4, 5/6 и так далее.

Но встерчаются и другие момента когда несмотря на то, что числитель больше знаменателя, все же ответ бует равен меньше единицы: 30/-15, или 40/-20 во всех случаях будет значениеи минусовое, а значит меньше единицы.

Когда в десятичной дроби впереди стоит 0, а за ним после запятой другие цифры, то такая дробь будет меньше единицы. А в случае правильной дроби числитель должен быть меньше знаменателя, тогда дробь будет меньше единицы.

Правильная дробь меньше единицы. Дроби разделяют на правильные и неправильные. Если у дроби числитель меньше знаменателя, то то такую дробь называют правильной дробью. В случае, если в дроби числитель больше знаменателя, то такая дробь называется неправильной.

Когда числитель обыкновенной дроби меньше знаменателя, тогда дробь будет меньше единицы. Или для отрицательных значений дроби. В случае десятичных дробей, если первая цифра 0, потом запятая и дальше идёт любая цифра.

Дроби, которые меньше единицы называются правильными дробями. А меньше единицы дроби, где числитель меньше знаменателя.

Такого человека можно назвать коммуникабельным. Коммуникабельные люди очень общительные, отзывчивые, редко обижаются. Они умеют интересно и конструктивно общаться, умеют устанавливать близкую связь между людьми.

Эта русская народная сказка сказка с традиционным сюжетом о девочке-сироте, у которой есть злая мачеха. Эта сказка известна и в обработке Л.Н. Толстого.

Мораль этой сказки перекликается с другими сказками, такими как “Морозко”, “Золушка”, “Двенадцать месяцев”: если быть добрым и бескорыстным, счастье всегда придёт к человеку, справедливость восторжествует, а зло будет наказано или останется без вознаграждения.

Жизнь дана на добрые дела.

Замечательная идея. Я бы деньги перевела, чем дарить букет цветов за 1500-2000 тысячи рублей. Цветы завянут, а детская жизнь хотябы одна спасется. Может какомо-то ребенку не хватает именно этих денег для лечения. Учительница молодец, хорошо придумала.

Прими́те и при́мете – это разные формы одного и того же глагола «приня́ть», обе написаны правильно.

Так же образованы формы повелительного наклонения, например, глаголов

• учить: уч-ат – уч+и (учи) +те (учи́те);

• решить: реш-ат – реш+и (реши) + те (реши́те);

• писать: пиш-ут – пиш+и (пиши) + те (пиши́те);

• прыгнуть: прыгн-ут – прыгн+и (прыгни) + те (пры́гните).

Концовки глаголов повелительного наклонения множественного числа и изъявительного наклонения 2-го лица множественного числа на письме ФОРМАЛЬНО СОВПАДАЮТ, если мы имеем дело с глаголами II спряжения, и НЕ СОВПАДАЮТ, если перед нами глаголы I спряжения:

• учить: Учи́те уроки вовремя – Когда у́чите уроки, будьте внимательны.

• решить: Реши́те задачи к завтрашнему дню – Когда решите задачи, можете немного отдохнуть.

• писать: Пиши́те письма – Когда пи́шете письма, не забывайте об этикетных формулах.

• прыгнуть: Пры́гните ещё раз – Когда пры́гнете, сами измерьте длину прыжка.

Источник

Сравнение дробей, как правильно

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.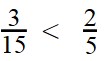

Источник

Правильные и неправильные дроби.

Виды дробей.

Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)

Делятся дроби на два вида правильные дроби и неправильные дроби.

В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)

В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)

Правильная дробь всегда меньше единицы. Рассмотрим пример:

Единицу мы можем представить как дробь \(1 = \frac<3><3>\)

Знаменатели одинаковые равны числу 3, далее сравниваем числители.

Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.

Может ли правильная дробь равна 1?
Ответ: нет.

Может ли неправильная дробь меньше 1?
Ответ: нет.

Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.

Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)

б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)

Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.

Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.

Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?

Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.

Источник

Урок 35 Бесплатно Правильные и неправильные дроби

На этом уроке мы вспомним, что такое обыкновенная дробь.

Рассмотрим, какие виды обыкновенных дробей существуют и выясним, какую дробь считают правильной, а какую неправильной и научимся сравнивать их.

Определим месторасположение правильной и не правильной дроби на координатном луче.

Разберем несколько задач на нахождение части целого и целого по его части, в которых часть представлена в виде обыкновенной неправильной дроби.

Правильные дроби

Вам уже известно, что дробь представляет собой часть некоторой величины.

Обыкновенная дробь записывается двумя числами, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).

Число, стоящее над дробной чертой, называют числителем.

Числитель показывает, сколько долей взяли от целого.

Число, стоящее под дробной чертой, называют знаменателем.

Знаменатель показывает, на сколько всего равных долей разделили целое.

Дробь можно получить следующим образом: разделить целое на равные части и взять несколько из этих частей.

В качестве примера рассмотрим такую ситуацию.

Плитку молочного шоколада разделили на 8 равных долек и из них взяли и съели 4.

Восемь долек шоколадки- это одна целая плитка шоколада.

Одна долька этой шоколадки представляет собой 1/8 всей плитки.

Четыре дольки из восьми можно записать дробью, получим дробь 4/8 (четыре восьмых).

Дробь 4/8 указывает на то, что целое разделили на восемь равных частей и из них взяли четыре.

8 (общее количество долей)- знаменатель дроби 4/8.

4 (количество долей, которые взяли)- числитель дроби 4/8.

Обратим внимание на члены этой дроби (числитель и знаменатель).

4 и 8– это два натуральных числа, причем если их сравнить, то мы можем заметить, что число 4 меньше 8, т.е. числитель меньше знаменателя.

Обыкновенная дробь, в которой числитель меньше знаменателя, называется правильной дробью.

Давайте выясним являются ли дроби 5/8, 6/8, 7/8 правильными.

Для данной дроби 5– это числитель, 8– это знаменатель.

Одну и ту же обыкновенную дробь можно представить разными способами.

Разделить целое на четыре части и взять две, будет тоже самое, что разделить это целое на две части и взять одну.

Такой же результат получится, если разделить все тоже целое на шесть равных частей и взять из них три и т.д.

Существует бесконечное множество дробей, равных половине целого.

Так, например, одна вторая получается, и в таких случаях: целое разделить на восемь частей и взять из них четыре (1/2 = 4/8), из десяти частей взять пять (1/2 = 5/10), из пятидесяти частей взять двадцать пять (1/2 = 25/50) и т.д.

Пройти тест и получить оценку можно после входа или регистрации

Неправильные дроби

Выясним, какую дробь называют неправильной на следующем примере:

На праздник купили один большой торт и разрезали его на девять одинаковых частей (9 долей).

Каждый гость съел по кусочку этого торта, в результате торта больше не осталось.

Получается, что гости съели девять кусочков торта из девяти возможных.

В таком случае дробь \(\mathbf<\frac<9><9>>\) будет показывать, что целое (весь торт) разделили на 9 долей и потом все эти 9 частей взяли, т.е. съели весь торт.

В данной дроби 9 (общее количество долей)- знаменатель дроби \(\mathbf<\frac<9><9>>\).

9 (количество долей, которые взяли)- числитель дроби \(\mathbf<\frac<9><9>>\).

Очевидно, что дробь \(\mathbf<\frac<9><9>>\) будет равна единице.

Любая дробь, в которой числитель равен знаменателю, равна единице.

Дробь \(\mathbf<\frac>\), где n = m, всегда равна единице.

Давайте выясним может ли обыкновенная дробь больше единицы.

Рассмотрим еще одну ситуацию.

Допустим, на праздник купили два одинаковых торта.

Каждый торт разрезали на девять равных частей.

За все время праздника гости съели 13 кусочков торта.

От второго торта осталось 5 несъеденных куска.

Когда разделили оба торта на 9 равных частей, в итоге получили 18 одинаковых кусочков (равных долей), они составляют два целых торта.

\(\mathbf<\frac<9><9>>\)– первый торт.

\(\mathbf<\frac<9><9>>\)– второй торт.

Получается из этих 18 кусочков съели 13, т.е. 1 целый торт и еще 4 кусочка.

Четыре кусочка от второго торта будут выражаться дробью \(\mathbf<\frac<4><9>>\).

В таком случае получаем \(\mathbf<\frac<9><9>>\) (один целый торт), да еще \(\mathbf<\frac<4><9>>\) второго торта- это часть кусочков торта, которые съели.

9 долей первого торта + 4 доли второго торта = \(\mathbf<\frac<13><9>>\) торта съели на празднике.

Так как каждый торт был разрезан на 9 частей, то в знаменателе дроби \(\mathbf<\frac<13><9>>\) стоит цифра 9.

Осталось пять частей торта, т.е. \(\mathbf<\frac<5><9>>\) торта- часть второго торта.

Обратите внимание на дроби \(\mathbf<\frac<9><9>>\) и \(\mathbf<\frac<13><9>>\).

В дроби \(\mathbf<\frac<9><9>>\) знаменатель равен 9 (общее количество долей), числитель равен 9 (количество долей, которые взяли).

9 = 9- числитель равен знаменателю.

В дроби \(\mathbf<\frac<13><9>>\) знаменатель равен 13 (общее количество долей), числитель равен 9 (количество долей, которые взяли).

13 > 9– числитель больше знаменателя.

Обыкновенную дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.

Правило: Любая неправильная дробь больше единицы или равна ей.

У меня есть дополнительная информация к этой части урока!

Необходимо понимать, что термин «неправильная» не говорит о том, что дробь неверная и с ней невозможно производить различные математические операции.

Дробь называют неправильной, так как она отличается от стандартного понимания дроби.

Неправильная дробь всегда содержит некоторую целую часть и дробную.

На следующих занятиях мы научимся выделять целую и дробную часть и производить с такими числами различные арифметические операции

Любое натуральное число можно представить в виде неправильной дроби, данная запись будет выглядеть так:

Дробь с числителем а, где а– любое натуральное число, и знаменателем, равным единице- это еще одна верная форма записи натурального числа а.

Натуральное число 3 = \(\mathbf<\frac<3><1>>\)

\(\mathbf<\frac<3><1>>\)- неправильная дробь, так как числитель (3) больше знаменателя (1).

\(\mathbf<\frac<24><1>>\)- неправильная дробь, так как числитель (24) больше знаменателя (1).

\(\mathbf<\frac<1245><1>>\)- неправильная дробь, так как числитель (1245) больше знаменателя (1).

Сравнивая правильную и неправильную дробь, можно однозначно сказать, что любая неправильная дробь больше правильной.

Определите какая из дробей \(\mathbf<\frac<7><8>>\) и \(\mathbf<\frac<8><7>>\) больше, какая меньше.

\(\mathbf<\frac<7><8>>\)– правильная дробь (числитель меньше знаменателя), а \(\mathbf<\frac<8><7>>\)– неправильная дробь (числитель больше знаменателя), следовательно \(\mathbf

В математике различают два вида обыкновенных дробей:

1. Правильная (числитель меньше знаменателя).

2. Неправильная дробь (числитель больше знаменателя или равен ему).

Выясним, где на координатном луче изображают правильные и неправильные дроби.

Любому дробному числу соответствует конкретное место на координатном луче.

Чтобы обозначить на координатном луче точку с координатой \(\mathbf<\frac>\), необходимо от начала координат отложить m отрезков, длина каждого такого отрезка должна составлять \(\mathbf<\frac<1>>\) от единичного отрезка.

Чтобы найти число \(\mathbf<\frac<1>>\), нужно единичный отрезок разделить на n равных частей.

Рассмотрим поясняющий пример.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.

Определим расположение точек A(\(\mathbf<\frac<2><6>>\)), B(\(\mathbf<\frac<11><6>>\)), D(\(\mathbf<\frac<6><6>>\)) на координатном луче.

Так как знаменатель каждой данной дроби равен шести, то разобьем единичный отрезок ОЕ на шесть равных частей-отрезков, каждая часть будет равна \(\mathbf<\frac<1><6>>\) ОЕ.

Правильная дробь \(\mathbf<\frac<2><6>>\) представляет собой две части (доли) из шести.

Следовательно, точка А(\(\mathbf<\frac<2><6>>\)) удалена от начала координат на расстояние двух отрезков, равных одной доле единичного отрезка- \(\mathbf<\frac<1><6>>\) ОЕ.

Отметим тот факт, что \(\mathbf<\frac<2><6>>\) правильная дробь, а это значит она меньше единицы.

На координатном луче данная точка располагается между числами 0 и 1, т.е. левее точки E(1).

Выясним, где на координатном луче будет располагаться точка D (\(\mathbf<\frac<6><6>>\)).

Известно, что дробь, у которой числитель равен знаменателю, представляет собой неправильную дробь, равную единице.

Дробь \(\mathbf<\frac<6><6>>\) означает шесть частей из шести- это единица.

Отметим точку D (\(\mathbf<\frac<6><6>>\)) на координатном луче, для этого отсчитаем 6 отрезков от начала координат, в результате попадаем в точку Е(1).

Точка с координатой \(\mathbf<\frac<6><6>>\) совпадает с точкой Е(1), в результате получаем сам единичный отрезок ОЕ.

Обозначим на координатном луче точку В с координатой \(\mathbf<\frac<11><6>>\).

Дробь \(\mathbf<\frac<11><6>>\) означает шесть частей (т.е. один единичный отрезок ОЕ) и еще пять таких частей.

Отложим от начала координат один единичный отрезок и от него отсчитаем еще пять делений, каждый из которых равен \(\mathbf<\frac<1><6>>\) единичного отрезка (в общем говоря, нам необходимо отсчитать от начала координат 11 делений, равных \(\mathbf<\frac<1><6>>\) ОЕ).

Нам несложно заметить, что неправильная дробь, у которого числитель больше знаменателя, лежит на координатном луче правее единицы.

На самом деле, такая неправильная дробь выражает некоторую целую часть, да еще часть целого.

Пройти тест и получить оценку можно после входа или регистрации

Источник