какая геометрическая фигура является разверткой сферы

ЛЕНТА ФЕДОРЕНКО – УСЛОВНАЯ РАЗВЕРТКА СФЕРЫ

Аннотация

В работе показан алгоритм построения разверток сложных поверхностей методами начертательной геометрии и продемонстрирована возможность формообразования сложных поверхностей из плоских разверток.

Ключевые слова: начертательная геометрия, развертка, сфера, торсовая поверхность

Введение

В технике, термином «развертка» называют плоскую заготовку, из которой получают объёмную форму детали или конструкции путём гибки. В современной промышленности развертки поверхностей широко применяются в различных видах производства, но особенно в тех, которые связаны с листовыми материалами: нефтехимическая и газовая промышленности (резервуары и трубопроводы), судостроение, авиастроение, легкая промышленность (швейная и кожевенная).

В данной работе под термином «развертка» будет пониматься плоская фигура, полученная при совмещении элемента развертываемой поверхности с плоскостью без разрывов и складок, при этом развертываемая поверхность рассматривается как гибкая, нерастяжимая пленка [1].

Прежде всего, необходимо определить основные термины и алгоритмы, поскольку в разных литературных источниках они различаются.

Все поверхности можно разделить на развертываемые и неразвертываемые. К первым относятся гранные поверхности и линейчатые поверхности, которые называются торсовыми. К торсовым поверхностям относятся цилиндрические, конические и поверхности с ребром возврата. Все остальные поверхности являются неразвертываемыми (например, сфера или тор).

Различают следующие виды разверток: точные, приближенные и условные.

Точные развертки можно получить только для многогранных поверхностей, поскольку такая развёртка есть совокупность многоугольников, конгруэнтных граням разворачиваемой поверхности и расположенных в одной плоскости [2].

Приближенные развертки используются при развертывании торсовых поверхностей. При этом криволинейные поверхности заменяются аппроксимирующей многогранной поверхностью. Например, цилиндрическая поверхность заменяется призмой. Однако, точная развертка такой призмы будет только приблизительно соответствовать развертке цилиндрической поверхности.

Для оставшихся неразвертываемых поверхностей производится построение условных разверток. Для этого применяется метод двойной аппроксимации. Сначала неразвертываемая поверхность разбивается на ряд отсеков. Каждый из этих отсеков заменяется (аппроксимируется) отсеком криволинейной развертываемой (торсовой) поверхности. Каждый отсек развертываемой поверхности аппроксимируется соответствующей ей многогранной поверхностью. И только после этого получают точную развертку многогранной поверхности, которая является условной разверткой неразвертываемой поверхности [3].

В литературе показано несколько стандартных способов создания разверток неразвертываемых поверхностей [4]. Например, поверхность сферы аппроксимируется отсеками цилиндрических поверхностей, которые потом заменяются призмами. В этом случае развертка будет выглядеть как набор двухдуговых «лепестков». Или сферическую поверхность заменяют элементами цилиндрических и конических поверхностей.

Иногда при создании развертки неразвертываемой поверхности аппроксимацию отсека элементом многогранника, заменяют на вырезание элемента самой криволинейной поверхности, как если бы материал поверхности был тканью.

Кроме этого, существуют и другие методы создания поверхностей, основанные на изгибании плоских заготовок [5, 6].

В промышленности же развертки больших сферических резервуаров состоят из меридианальных лепестков и купола с днищем в виде двух сферических сегментов. Купол и днище резервуара получают из металлического диска путем обжатия на оправке с помощью молота или пресса. Лепестки изготавливаются на многовалковом стенде методом холодного вальцевания, то есть гибки металла до нужной формы или используется метод горячей штамповки, то есть изгибают в двух плоскостях.

Таким образом, можно сделать вывод, что создать неразвертываемую поверхность из плоской развертки очень сложно. Повышение геометрической точности такой поверхности ведет к увеличению количества элементов (отсеков) поверхности, что отрицательно скажется на экономической составляющей процесса изготовления и прочностных характеристиках объекта. Поэтому создание новых способов развертывания сложных поверхностей является актуальной задачей.

Постановка задачи

Для решения поставленной задачи необходимо заменить (аппроксимировать) поверхность сферы некой развертываемой поверхностью. Из курса начертательной геометрии известно, что любая поверхность может быть задана как множество последовательных положений некоторой движущейся в пространстве линии. Такая линия называется образующей. Закон перемещения образующей в пространстве и изменения её формы задаются направляющими линиями.

Образующие линии торсовой поверхности удобнее всего расположить в меридиональных плоскостях сферы (рис.1б). Необходимо отметить, что длина образующей линии получаемой торсовой поверхности постоянна, кроме двух околополюсных оборотов направляющей линии, где длина образующей будет переменна (это если применять спираль Клелия).

На втором этапе заменяем (аппроксимируем) торсовую поверхность многогранником. Для этого необходимо заменить направляющую кривую ломаной линией (рис.2). Однако, возможности компьютерных графических пакетов позволяют обратно “скривить” такие ломаные линии, достаточно задать на каждой скрутке (обороте) спирали несколько тысяч опорных точек.

На третьем этапе произведем точное построение развертки многогранника.

Для построения развертки многогранной поверхности нужно совместить все грани этой поверхности с одной плоскостью так, чтобы образовалась плоская фигура. При этом смежными будут две грани, имеющие общее ребро.

Для одной и той же поверхности вид ее развертки может быть различным в зависимости от избранной последовательности расположения граней на развертке.

При этом самая красивая условная развертка сферы получается, если мысленный “разрез” многогранника произвести по бывшей направляющей спирали (криволинейной или ломаной).

Процедура построения развертки построена на применении способа триангуляции. Построение начинается с самой маленькой грани, расположенной около полюса сферы, и раскручивается по спирали до аналогичной грани на другом полюсе. Расположение граней и их форма наглядно показаны на рис. 2.

Построение развертки сферы производилось в графическом пакете AutoCAD с использованием программы написанной на языке AutoLISP [7]. Результат построения развертки показан на рис. 3.

Первый опытный образец сферы из ленточной развертки показан на рис.4.

По аналогичному алгоритму были построены условные развертки торовой и параболической поверхностей.

Результаты работы применяются автором при чтении лекций по курсу «Начертательная геометрия» в разделе «Развертки поверхностей», а опытный образец из металла, изготавливается в настоящее время на заводе фирмы «Соединительные детали трубопроводов» в г. Таганроге для последующей проверки на прочность.

Ещё один результат данной работы – при задании в программе большого числа витков направляющей спирали, лента развертки утончается и фактически преобразуется в спираль Корню.

Список литературы

Рисунки к докладу

Спираль Клелия (а) и аппроксимация сферы торсовой поверхностью (б)

Рис. 2

Аппроксимация торсовой поверхности многогранником

Рис. 3

Условная развертка сферической поверхности

Рис. 4

Вопросы и комментарии к выступлению:

Владимир Игоревич, здравствуйте! Какие у Вас замечательные, красивые и действительно полезные исследования! Интересно будет почитать результаты после испытаний.

С уважением, Кокарева Я.А.

Хейфец Александр Львович
(24 марта 2017 г. 20:51)

Владимир Игоревич, решение красивое, современное, все так. Но ….

Наберите в поисковике Сфера Эшера и познакомьтесь с искусством этого дизайнера с мировым именем. Конкретно по данной работе можно набрать:

Увидите практически Вашу развертку.

Более того,извините, но есть и моя работа на эту тему: А.Л. Хейфец. Инженерная компьютерная графика. AutoCAD. – СПб., БХВ, 2005. – 336 с.

С уважением. А.Л. Хейфец.

Нельзя не согласиться с Александром Олеговичем, что работа очень интересная и, одновременно, с его вполне резонным вопросом о защите авторства.

Лента очень похожа на сферу Эшера, наверное, и на работу Александра Львовича, но можно заметить, что есть и отличия, причем с точки зрения технического осуществления, их можно даже назвать существенными.

Владимир Игоревич не приводит информации о правовой защите названия, но обычно имя автора принято давать, если есть патент на изобретение, полезную модель, промышленный образец. На сайте ФИПС есть информация о 3214 изобретениях со словом лента в названии, но ленты Федоренко поиск не дает. Если заявка не подавалась, то надо подавать срочно, данная публикация может помешать получению охранного документа.

Конечно, в научном труде надо приводить ссылки на аналогичные работы, но умышленного нарушения ведь здесь нет. Поэтому хочется поддержать и поблагодарить Владимира Игоревича за информацию, особенно приятно, что лента воплощается в металле, что само по себе уникальный случай.

С уважением Головнин А.А.

Федоренко Владимир Игоревич
(25 марта 2017 г. 1:34)

Уважаемый Александ Олегович!

Статью я опубликовал по просьбе коллеги по работе Полубинской Людмилы Георгиевны. Да и самому очень хотелось показать работу специалистам. Может чуть рано, зато познакомился (пусть заочно) с замечательными учеными.

Заявка на изобретение подана, но Фамилию с ленты могут снять, как сняли ее когда-то с роторно-волнового компрессора

Извинете, что кратко. С уважением, Федоренко В.И.

Федоренко Владимир Игоревич
(25 марта 2017 г. 2:36)

Уважаемый Александр Львович!

Спасибо, что назвали решение красивым. После Вашей анимации, это дорогого стоит.

С творчеством Эшера знаком достаточно хорошо, и даже когда-то давно пытался ему подражать в разработке рисунка паркета и мозаики. «Мы все учились понемногу. «

Попробую определить наиболее удобный источник.

Я обязательно буду делать ссылку на Ваши работы

Я в сферу (каламбур получился) НГ перешел недавно, спасибо, что поправили.

С уважением, Федоренко В.И.

Владимир Игоревич, не обижайтесь, но я насчитал в Вашей литературе 11 геометров, а не 2. То есть, 11 фамилий ученых, занимавшихся или занимающихся геометрией.

А развертка получилась прикольная,я такой еще не встречал.

С уважением, Н. Сальков.

Федоренко Владимир Игоревич
(25 марта 2017 г. 3:06)

Уважаемый Алексей Алексеевич!

Другой вопрос, что мало. Но у меня список был большой, только односторонний.

С уважением, Федоренко В.И.

Федоренко Владимир Игоревич
(25 марта 2017 г. 15:18)

Уважаемый Николай Андреевич!

Вот и здесь, не сумел правильно выразить мысль. Не все ученые, фамилии которых я указал, занимаются вопросами построения и исследования торсовых поверхностей.

Кстати, есть более прикольная развертка и Вы ее тоже еще не видели. Но, формат доклада ограничен 4-мя рисунками.

А мы люди законопослушные.

С уважением, Федоренко В.И.

Федоренко Владимир Игоревич
(25 марта 2017 г. 15:41)

Добрый день, Яна Андреевна!

Спасибо за добрые слова о моей работе. Если два разных человека говорят, что результат работы красивый, то значит он правильный.

Источник

Развертка (выкройка) сферы

Развертка сферы на плоскость. Калькулятор вычисляет основные параметры развертки, а также выводит координаты точек для построения развертки одной доли.

Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.

Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.

Развертка сферы

С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:

Радиус дуги можно вычислить по длине хорды (это а) и высоте сегмента (это h=b/2) по следующей формуле (см. Сегмент круга).

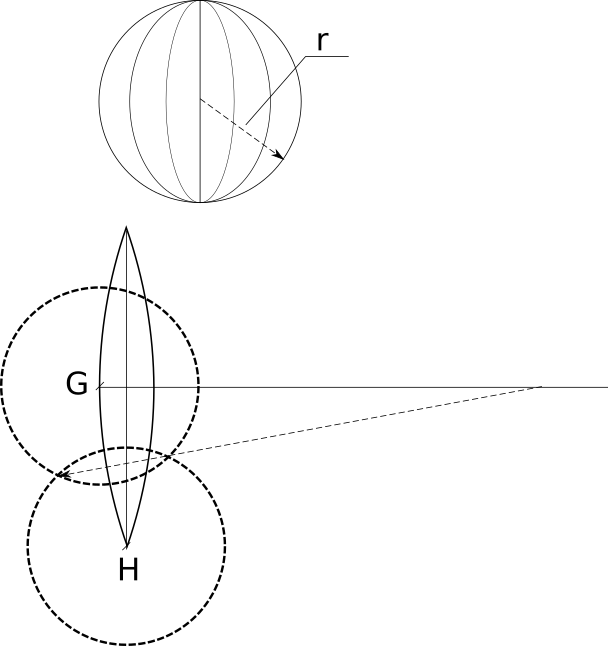
В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.

Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.

Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:

Источник

Развертка сферической поверхности

Развертка сферической поверхности

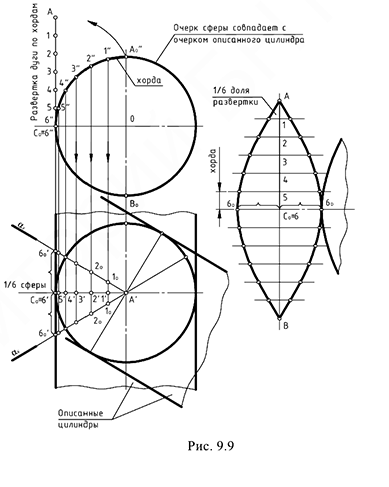
На рис. 9.9 показано построение условной развертки сферической поверхности.

Поверхность сферы условно разрезают на ка-кое-то количество частей (6, 12 и более) и каждую часть заменяют (аппроксимируют) цилиндрической описанной поверхностью, фронтальная проекция которой совпадает с фронтальным очерком сферы — окружностью.

Далее выполнятся развертка одной доли поверхности сферы как сектора цилиндрической поверхности по следующему графическому алгоритму:

1-е действие. На горизонтальной проекции разрезать поверхность сферы на 6 частей и рассмотреть эту 1/6 часть (сектор) как фронтально-проецирующий цилиндр, описанный вокруг сферы.

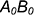
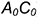
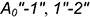
2-е действие. Разделить дугу очерковой окружности сферы, которая совпадает с окружностью описанного цилиндра, на 12 частей (поскольку есть симметрия, рассматриваем дугу ) и заменить участки хордами (то есть вписать 12-угольную призму) — и т. д.

3-е действие. Спроецировать точки 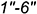на стороны взятого сектора его горизонтальной проекции.

4-е действие. Свободном поле чертежа провести вертикальную линию и отложить от точки 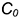вверх и вниз по 6 отрезков, равных величине хорд (точки пронумеровать).

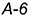
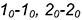
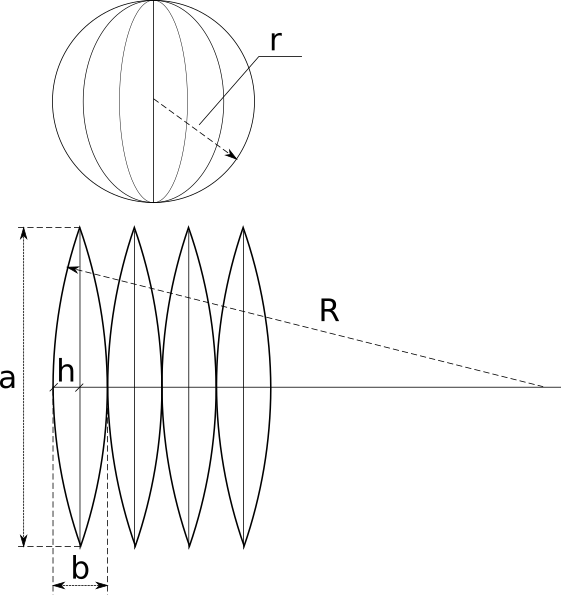
5-е действие. Через каждую построенную точку провести горизонтальные линии и на каждой отложить величину соответствующей образующей: и т. д.

6-е действие. Конечные точки соединить лекальной кривой.

Таким образом построена 1/6 доля условной поверхности сферы, а 6 таких долей составят развертку всей поверхности.

С увеличением количества долей (1/12, 1/24 и т. д.) точность развертки увеличивается.

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Геометрические фигуры. Шар, сфера.

Понятие шара в метрическом пространстве естественным образом обобщает понятие шара в евклидовой геометрии.

Радиус AO и диаметр AB находят тем же способом, что и для окружности.

Сфера является поверхностью (границей) шара с центром и радиусом, как у сферы.

Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга/круга около диаметра.

Любое плоское сечение шара является кругом. Чем ближе секущая плоскость к центру шара, тем радиус круга становится больше. Самый большой круг оказывается при прохождении плоскости через центр O. Этот круг разделяет шар на две равные части и он называется большим кругом. Радиус большого круга равен радиусу шара.

Меридианы шара (сферы).

Сквозь 2 точки шара, которые лежат на концах общего диаметра, возможно провести бесконечное число больших кругов — меридианов. Через 2 точки, которые не на концах общего диаметра шара возможно провести всего лишь 1 большой круг.

Основные геометрические формулы шара (сферы).

Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:

Определения, связанные с понятием шара.

Предположим, дано метрическое пространство (X, ρ). Значит:

Замкнутый шар с центром в x₀ и радиусом r можно выразить так:

Свойства шара.

S_цил и V_цил – полная поверхность и объём описанного цилиндра вокруг шара.

Части шара.

Формулу объёма шара можно объяснить следующими рассуждениями. В шаре возможно разместить огромное количество пирамид с очень маленькими основаниями, разместив пирамиды таким образом, чтобы их вершины располагались в центре шара, а основания лежали бы на поверхности шара и эти пирамиды соприкасались бы боковыми гранями.

Высота любой построенной пирамиды приблизительно равна радиусу (R) шара. Если не обращать внимание различиями этих длин, то объём (v) всех пирамид отдельно можно представить такой формулой:

Значит, сумма объёмов (V’) пирамид выразим формулой:

Сумма (S’) очень близка к площади поверхности шара (S).

Сумма объёмов всех пирамид (V’) приблизительно равна объёму (V) шара. Если не обращать внимание на незначительные различия в этих величинах, тогда получится такая формула:

которая показывает, что объём шара соответствует 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.

где D — диаметр шара.

Примечание. В формуле V = 1/3 SR поставлен знак точного, а не приближённого равенства, хотя на основании проведённых рассуждений можно было принять его приближённым, хотя в старших классах средней школы доказываем, что равенство V = 1/3 SR точное, а не приближённое.

Источник

Реферат по дисциплине «Графика» на тему «Развертки поверхностей геометрических тел. Построение точных и условных разверток»

МБОУ Сухо – Сарматская СОШ

на тему « Развертки поверхностей геометрических тел. Построение точных и условных разверток »

Выполнила учитель технологи по направлению «Технология» Шаповалова И.Н.

Основные свойства развертки

Развертка поверхности многогранников

Развертка цилиндрической поверхности

Развертка конической поверхности

Список использованной литературы

С развертками поверхностей мы часто встречаемся в обыденной жизни, на производстве и в строительстве. Чтобы изготовить футляр для книги (рис. 169), сшить чехол для чемодана, покрышку для волейбольного мяча и т. п., надо уметь строить развертки поверхностей призмы, шара и других геометрических тел. Разверткой называется фигура, полученная в результате совмещения поверхности данного тела с плоскостью. Для одних тел развертки могут быть точными, для других — приближенными. Точные развертки имеют все многогранники (призмы, пирамиды и др.), цилиндрические и конические поверхности и некоторые другие. Приближенные развертки имеют шар, тор и другие поверхности вращения с криволинейной образующей. Первую группу поверхностей будем называть развертывающимися, вторую — неразвёртывающимися.

Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

2. Основные свойства развертки

1. Длины двух соответствующих линий поверхности и ее развертки равны между собой;

2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

3. Прямой на поверхности соответствует также прямая на развертке;

4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

5. Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.

3.Развертка поверхности многогранников

Разверткой многогранной поверхности называется плоская фигура,получаемая последовательным совмещением всех гранейповерхности с плоскостью.

Существует три способа построения развертки многогранных поверхностей:

1. Способ нормального сечения;

3. Способ треугольника.

4. Развёртка пирамиды

Рисунок 1. Пирамида и её развертка

Рисунок 2. Определение истинной величины основания и ребер пирамиды

Алгоритм построения можно сформулировать следующим образом ( рис.2 ):

1. Определяют натуральную величину основания пирамиды (например методом замены плоскостей проекций);

2. Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S );

3. Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рис.8.42).

Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки.

Рисунок 3. Построение развертки пирамиды

В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.

Рисунок 4. Развертка призмы способом нормального сечения

Развертка призмы, частный случай, когда основание призмы наодну из плоскостей проекций проецируется в натуральную величину (рис.5).

Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.

Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П ₄ и проходящую через ребро С ₄ F ₄ .

Рисунок 5. Развертка призмы способом раскатки.

6. Развертка цилиндрической поверхности

Рисунок 6. Развертка цилиндрической поверхности.

7.Развертка конической поверхности

Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду ( рис.7 ).

Рисунок 7. Развертка конической поверхности.

8. Построение условных разверток неразвертывающихся поверхностей

Развертку неразвертывающейся поверхности построить нельзя. Для построения условной развертки такой поверхности применяют метод аппроксимации, который заключается в следующем.

Данная неразвертываюшаяся поверхность Ф разбивается на некоторые отсеки. Каждый из этих отсеков заменяется отсеком кривой развертывающейся поверхности. Совокупность всех отсеков развертывающихся поверхностей называется обводом Ф’ поверхности Ф. С помощью триангуляции обвод Ф’ заменяется обводом Ф» гранных поверхностей. Развертка гранных поверхностей, образующих обвод Ф», принимается за условную развертку поверхности Ф. При свертывании такой развертки, кроме изгибания, необходимо произвести частичное растяжение или сжатие отдельных ее участков.

Построение развертки сферы

Сферическая поверхность является неразвертывающейся. Существующие методы построения ее развертки дают лишь приближенные результаты.

Сущность одного из них заключается в том, что элемент сферической поверхности заменяется элементом цилиндрической поверхности касательной к сфере по главному меридиану m. Ось такой цилиндрической поверхности проходит через центр сферы перпендикулярно G _2. При этом под элементом сферы понимают часть ее, ограниченную двумя большими окружностями.

Для выполнения построения развертки поверхность сферы необходимо:

2) описать вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно к П ₂ ;

4) для построения развертки цилиндрического элемента (лепестка) разделить его фронтальную проекцию на восемь равных частей;

8) соединить плавной кривой концы отрезков, в результате чего получится развертка верхней половины лепестка.

Длину этой дуги S ₂ = К ₂ ´ М ₂ нужно откладывать на развертке от экватора соответствующего лепестка по вертикальной оси симметрии.

Рисунок 8. Построение развертки сферы

10.Построение развертки цилиндрической поверхности

.

Рисунок 9. Построение развертки цилиндрической поверхности

Взято с сайта http://fet.mrsu.ru/text/distance/books/Engineering_graphics/aster/GLAWA_7.htm

Многие изделия и детали нередко содержат фасонные элементы сложных геометрических форм из листового материала. Изготовление их требует построения разверток.

Умение построения разверток имеет огромное практическое значение при конструировании различных изделий из листового материала. Часто приходится изготавливать не только развертывающиеся поверхности, но и неразвертыващиеся. В этом случае последние разбивают на части, которые можно приближенно заменить развертывающимися поверхностями (цилиндрическими, коническими, многогранными), а затем строят развертки этих частей.

Список использованной литературы

Левицкий В.С. «Машиностроительное черчение» М.: Высшая школа 1988г.-331 с.

В.А. Антипов «Начертательная геометрия. Курс лекций для студентов» Самара: СамГАПС, 2005 – 55 с.

Источник

• ← какая водка лучше кремлин или белуга
• коды ошибок mitsubishi electric mr slim →