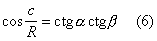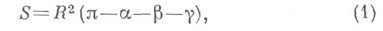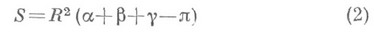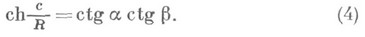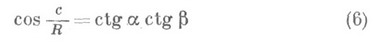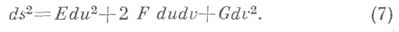какая геометрическая система является альтернативной геометрии евклида
Евклидова (элементарная) геометрия
Евклидова геометрия — это геометрическая теория, основанная на системе аксиом, которая была впервые изложена в третьем веке до нашей эры великим древнегреческим математиком Евклидом в грандиозном научном труде «Начала».
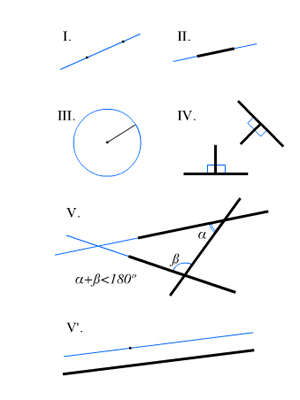
Система аксиом Евклида базируется на основных геометрические понятиях таких, как точка, прямая, плоскость, движение, а также на следующие отношения: «точка лежит на прямой на плоскости», «точка лежит между двумя другими».
В «Началах» Евклид представил следующую аксиоматику:
Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.
В современной трактовке система аксиом Евклида может быть разделена на пять групп:
Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.
Неевклидовы геометрии
Полезное
Смотреть что такое “Неевклидовы геометрии” в других словарях:
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — геометрические системы, отличные от евклидовой геометрии. Среди неевклидовых геометрий особое значение имеет Лобачевского геометрия … Большой Энциклопедический словарь
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в буквальном понимании все геометрич. системы, отличные от геометрии Евклида; однако обычно термин Н. г. применяется лишь к геометрич. системам (отличным от геометрии Евклида), в к рых определено движение фигур, причем с той же степенью свободы,… … Математическая энциклопедия
неевклидовы геометрии — геометрические системы, отличные от евклидовой геометрии. Среди неевклидовой геометрии особое значение имеет Лобачевского геометрия. * * * НЕЕВКЛИДОВЫ ГЕОМЕТРИИ НЕЕВКЛИДОВЫ ГЕОМЕТРИИ, геометрические системы, отличные от евклидовой геометрии.… … Энциклопедический словарь
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — геом. системы, отличные от евклидовой геометрии. Среди Н. г. особое значение имеет Лобачевского геометрия … Естествознание. Энциклопедический словарь
История математики — История науки … Википедия
Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия
Лобачевского геометрия — геометрическая теория, основанная на тех же основных посылках, что и обычная Евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит:… … Большая советская энциклопедия
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — геометрия, основанная на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных (см. Пятый постулат). В евклидовой геометрии согласно этой аксиоме на плоскости через точку Р, лежащую вне прямой А А, проходит… … Математическая энциклопедия
Римана геометрия — эллиптическая геометрия, одна из неевклидовых геометрий (См. Неевклидовы геометрии), т. е. геометрическая теория, основанная на аксиомах, требования которых (в значительной части) отличны от требований аксиом евклидовой геометрии (См.… … Большая советская энциклопедия
Неевклидова геометрия
Неевклидова геометрия — в буквальном понимании — любая геометрическая система, отличная от геометрии Евклида; однако традиционно термин «неевклидова геометрия» применяется в более узком смысле и относится только к двум геометрическим системам: геометрии Лобачевского и сферической геометрии.
Как и евклидова, эти геометрии относятся к метрическим геометриям пространства постоянной кривизны. Нулевая кривизна соответствует евклидовой геометрии, положительная — сферической, отрицательная — геометрии Лобачевского.
Содержание
Метрика для плоскости
Вид метрики для однородных планиметрий зависит от выбранной системы (криволинейных) координат; далее приводятся формулы для случая полугеодезических координат:
История понятия
См. также
Литература
| Геометрия | Алгебраическая геометрия • Аналитическая геометрия • Евклидова геометрия • Неевклидова геометрия • Планиметрия • Стереометрия • Тригонометрия |
|---|---|
| Топология | Общая топология • Алгебраическая топология |
| Смежные направления | Дифференциальная геометрия и топология • Геометрическая топология |
Полезное
Смотреть что такое “Неевклидова геометрия” в других словарях:
НЕЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера
Неевклидова геометрия — см. Геометрия, Лобачевский и Пангеометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
неевклидова геометрия — неевкл идова геом етрия, неевкл идовой геом етрии … Русский орфографический словарь
неевклидова геометрия — … Орфографический словарь русского языка
неевклидова — (геометрия) … Орфографический словарь-справочник
Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия
Геометрия — (от др. греч. γῆ Земля и μετρέω «мерю») раздел математики, изучающий пространственные структуры, отношения и их обобщения[1]. Содержание … Википедия
Геометрия Римана — Не следует путать с Риманова геометрия. Геометрия Римана (эллиптическая геометрия) одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой… … Википедия
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
неевклидова — *неевкли/дова (геометрия) … Слитно. Раздельно. Через дефис.
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
Неевклидовы геометрии как синтетические теории. Геометрия Лобачевского строится на основе тех же аксиом, что и евклидова, за исключением только одной аксиомы о параллельных. Именно, согласно аксиоме о параллельных евклидовой геометрии через точку, не лежащую на данной прямой а, проходит точно одна прямая, к-рая лежит в одной плоскости с прямой аи не пересекает эту прямую; в геометрии Лобачевского принимается, что таких прямых более одной (затем доказывается, что их бесконечно много).
В геометрии Рпмана принимается аксиома: каждая прямая, лежащая в одной плоскости с данной прямой, пересекает эту прямую. Эта аксиома противоречит системе аксиом евклидовой геометрии с исключением аксиомы о параллельных. Таким образом, система аксиом, лежащая в основе геометрии Римана, необходимо должна отличаться от системы аксиом евклидовой геометрии не только заменой одной аксиомы о параллельных другим утверждением, но и части остальных аксиом. Различными в этих геометриях являются аксиомы, к-рые служат для обоснования т. н. отношений порядка геометрия, элементов. Сущность дела в следующем: в евклидовой геометрии и в геометрии Лобачевского порядок точек на прямой является линейным, т. е. подобным порядку во множестве действительных чисел; в геометрии Римана порядок точек на прямой является циклическим, т. е. подобным порядку во множестве точек окружности. Кроме того, в геометриях Евклида и Лобачевского каждая прямая, лежащая в данной плоскости, разделяет эту плоскость на две части; в геометрии Римана прямая не разделяет плоскость на две части, т. е. любые две точки плоскости, не лежащие на данной прямой, можно соединить в этой плоскости непрерывной дугой, не пересекая данную прямую (топологич. моделью плоскости Римана служит проективная плоскость).
Требования аксиом, определяющих движение фигур, для всех трех геометрий одинаковы.
Примеры теорем Н. г,
1) В геометрии Лобачевского сумма внутренних углов любого треугольника меньше двух прямых; в геометрии Римана эта сумма больше двух прямых (в евклидовой геометрии она равна двум прямым).
2) В геометрии Лобачевского площадь треугольника выражается формулой
где 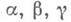
при аналогичном значении символов (в евклидовой геометрии зависимости между площадью треугольника и суммой его углов нет).
3) В геометрии Лобачевского между сторонами и углами треугольника существует ряд зависимостей, напр.:
При нек-ром согласовании линейного масштаба и единицы измерения площадей постоянная Rв формулах (1), (3), (4) будет одинаковой. Число Rназ. радиусом кривизны плоскости (или пространства) Лобачевского. Число Rпри данном масштабе выражает определенный отрезок в плоскости (пространстве) Лобачевского, к-рый также называют радиусом кривизны. Если масштаб меняется, то меняется число R, но радиус кривизны, как отрезок, остается неизменным. Если радиус кривизны принять за масштабный отрезок, то R=1. В геометрии Римана существуют сходные равенства:
(для произвольного треугольника) и
(для прямоугольного) при аналогичном значении символов. Число Rназ. радиусом кривизны плоскости (или пространств а) Римана. Как видно из формул (4) и (6), в каждой из Н. г. гипотенуза прямоугольного треугольника определяется его углами; более того, в Н. г. стороны любого треугольника определяются его углами, т. е. не существует подобных треугольников, кроме равных (в евклидовой геометрии нет формул, аналогичных формулам (4) и (6), и нет никаких других формул, выражающих линейные величины через угловые). При замене R на iR формулы (1), (3), (4) превращаются в формулы (2), (5), (6); вообще, при замене Rна iR все метрич. формулы геометрии Лобачевского (сохраняющие при этой замене геометрич. смысл) переходят в соответствующие формулы геометрии Римана. При 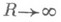
Неевклидовы геометрии в плане дифференциальной геометрии. В каждой из Н. г. дифференциальные свойства плоскости аналогичны дифференциальным свойствам поверхностей евклидова пространства; именно: в неевклидовой плоскости могут быть введены внутренние координаты и, v так, что дифференциал ds дуги кривой, соответствующей дифференциалам 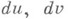
Пусть, в частности, в качестве координаты ипроизвольной точки Мберется длина перпендикуляра, опущенного из Мна фиксированную прямую, а в качестве координаты v- расстояние от фиксированной точки Оэтой прямой до основания указанного перпендикуляра; величины и, v следует брать со знаком, подобно обычным декартовым координатам. Тогда формула (7) для плоскости Лобачевского будет иметь вид
а для плоскости Римана
Так как метрич. форма определяет внутреннюю геометрию поверхности, то при такой замене и другие метрич. соотношения геометрии Лобачевского переходят в метрич. соотношения.
СОДЕРЖАНИЕ
История
Задний план
Если прямая линия попадает на две прямые таким образом, что внутренние углы на одной стороне вместе меньше двух прямых углов, тогда прямые линии, если они образуются бесконечно, пересекаются на той стороне, на которой углы меньше, чем два прямых угла.
Другие математики придумали более простые формы этого свойства. Однако, независимо от формы постулата, он постоянно кажется более сложным, чем другие постулаты Евклида :
1. Провести прямую линию из любой точки в любую точку.
2. Построить [удлинить] конечную прямую линию непрерывно в прямую.
3. Описать круг с любым центром и расстоянием [радиусом].
4. Все прямые углы равны друг другу.
Джордано Витале в своей книге Euclide restituo (1680, 1686) использовал четырехугольник Саккери, чтобы доказать, что если три точки равноудалены на основании AB и вершине CD, то AB и CD везде равноудалены.
В работе под названием Euclides ab Omni Naevo Vindicatus ( Евклид, свободный от всех недостатков ), опубликованной в 1733 году, Саккери быстро отбросил эллиптическую геометрию как возможность (некоторые другие аксиомы Евклида должны быть изменены, чтобы эллиптическая геометрия работала) и принялся за работу, доказывая, что большое количество результатов по гиперболической геометрии.
В конце концов он достиг точки, когда он считал, что его результаты демонстрируют невозможность гиперболической геометрии. Его утверждение, по-видимому, было основано на предположениях Евклида, поскольку не было логического противоречия. В этой попытке доказать евклидову геометрию он вместо этого непреднамеренно открыл новую жизнеспособную геометрию, но не реализовал ее.
В то время было широко распространено мнение, что Вселенная работает в соответствии с принципами евклидовой геометрии.
Открытие неевклидовой геометрии
Терминология
Есть математики, которые по-разному расширяют список геометрий, которые следует называть «неевклидовой».