какая кривая называется выпуклой на интервале
Какая кривая называется выпуклой на интервале
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
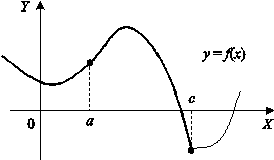
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ”(x) 0 – вогнутый.
Доказательство. Предположим для определенности, что f”(x) Î (a; b) и проведем через точку M0 касательную. Ее уравнение 
Итак, уравнение кривой имеет вид y = f(x). Обозначим 


Разность f(x) – f(x0) преобразуем по теореме Лагранжа 

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ”(x0) = 0 или f ”(x0) не существует и при переходе через значение x = x0 производная f ”(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ”(x) 0 при x > x0. Тогда при x x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ”(x) > 0 при x x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
Найдем производные заданной функции до второго порядка.


Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
Возможные точки перегиба найдем, решив уравнение 2x 2 – 1 = 0. Отсюда 
Точки перегиба 




Следовательно, f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. 



Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Так как 
Прямая x = 0 – вертикальная асимптота.
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда 
Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию 


Следовательно, мы можем записать следующее равенство 
Так как x → +∞, то должно выполняться равенство 




Если число k уже известно, то 

Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство 
Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.
Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы

Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
x = 0 – вертикальная асимптота.

а) 
Итак, при x → +∞ наклонная асимптота у= х.
б) 
а) 


б) 

Выпуклость функции. Направление выпуклости. Точки перегиба. Условия выпуклости и перегиба.
Когда мы чертим график функции, важно определить интервалы выпуклости и точки перегиба. Они, наряду с промежутками убывания и возрастания, нужны нам для четкого представления функции в графическом виде.
Понимание этой темы требует знания того, что такое производная функции и как ее вычислить до некоторого порядка, а также умения решать разные виды неравенств.
В начале статьи определяются основные понятия. Потом мы покажем, какая связь существует между направлением выпуклости и значением второй производной на определенном интервале. Далее мы укажем условия, в которых можно определить точки перегиба графика. Все рассуждения будут проиллюстрированы примерами решений задач.
Что такое выпуклость/вогнутость функции и точки перегиба графика функции
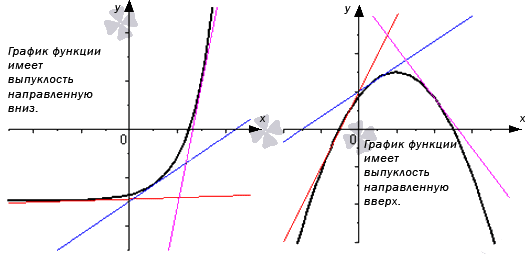
Дифференцируемая функция является выпуклой по направлению вниз на некотором интервале в том случае, когда ее график располагается не ниже касательной к нему в любой точке этого интервала.
Дифференцируемая функция является выпуклой по направлению вверх на некотором интервале в том случае, если график данной функции располагается не выше касательной к нему в любой точке этого интервала.
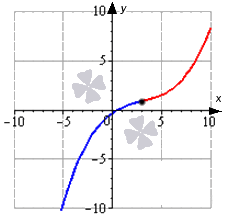
Выпуклую вниз функцию можно иначе назвать вогнутой. Оба определения наглядно показаны на графике ниже:
Проще говоря, точка перегиба – это место на графике, в котором есть касательная, и направление выпуклости графика при прохождении через это место будет менять направление выпуклости. Если вы не помните, при каких условиях возможно существование вертикальной и невертикальной касательной, советуем повторить раздел о касательной графика функции в точке.
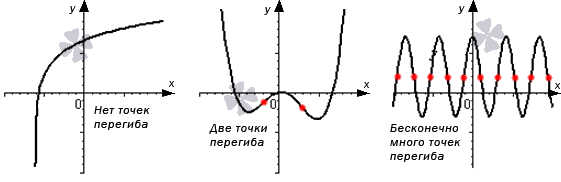
Ниже указан график функции, имеющей несколько точек перегиба, которые выделены красным. Уточним, что наличие точек перегиба не является обязательным. На графике одной функции их может быть одна, две, несколько, бесконечно много или ни одной.
Как найти интервалы выпуклости функции
В этом пункте мы расскажем о теореме, с помощью которой можно определить промежутки выпуклости на графике конкретной функции.
График функции будет иметь выпуклость по направлению вниз или вверх в том случае, если у соответствующей ему функции y = f ( x ) будет вторая конечная производная на указанном интервале x при условии, что неравенство f ” ( x ) ≥ 0 ∀ x ∈ X ( f ” ( x ) ≤ 0 ∀ x ∈ X ) будет верным.
Используя данную теорему, можно найти промежутки вогнутости и выпуклости на любом графике функции. Для этого нужно просто решить неравенства f ” ( x ) ≥ 0 и f ” ( x ) ≤ 0 на области определения соответствующей функции.
Уточним, что те точки, в которых вторая производная не существует, но функция y = f ( x ) определена, будут включаться в интервалы выпуклости и вогнутости.
Посмотрим на примере конкретной задачи, как правильно применять эту теорему.
Решение
Областью определения данной функции является все множество действительных чисел. Начнем с вычисления второй производной.
Для наглядности изобразим график функции и отметим на нем выпуклую часть синим, а вогнутую – красным цветом.
А что же делать в случае, если область определения второй производной не совпадает с областью определения функции? Здесь нам пригодится замечание, сделанное выше: те точки, где конечная вторая производная не существует, мы тоже будем включать в отрезки вогнутости и выпуклости.
Решение
Для начала выясним область определения функции.
Теперь вычисляем вторую производную:
Нанесем получившиеся точки на график и определим знак выражения на всех интервалах, которые войдут в область определения исходной функции. На графике эта область обозначена штриховкой. Если значение положительно, отмечаем интервал плюсом, если отрицательно, то минусом.
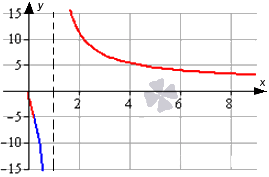
Изобразим график, отметив на нем выпуклую часть синим, а вогнутую красным цветом. Вертикальная асимптота отмечена черным пунктиром.
Условия перегиба графика функции
Начнем с формулировки необходимого условия перегиба графика некоторой функции.
Первое достаточное условие существования точки перегиба графика функции
Все сказанное выше удобно представить в виде последовательности действий.
Как найти точки перегиба графика функции
Для наглядности разберем две задачи.
Решение
Указанная функция определена на всем множестве действительных чисел. Считаем первую производную:
Вычисляем вторую производную:
Далее определяем, когда она будет обращаться в 0 :
Дуги показывают направление выпуклости графика в каждом интервале.
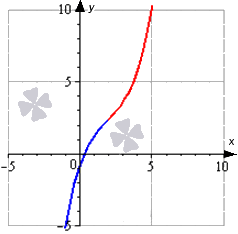
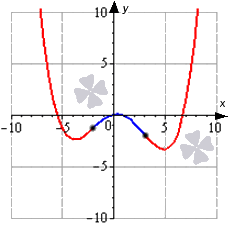
Решение задачи наглядно изображено на графике: синий цвет – выпуклости, красный – вогнутость, черный цвет означает точки перегиба.
Решение
Область определения заданной функции – множество всех действительных чисел. Вычисляем производную:
Это значит, что через данную точку будет проходить вертикальная касательная к графику. Следовательно, 3 может быть абсциссой точки перегиба.
Вычисляем вторую производную. Также находим область ее определения и точки, в которых она обращается в 0 :
У нас получились еще две возможные точки перегиба. Нанесем их все на числовую прямую и разметим получившиеся интервалы знаками:
Перемена знака будет происходить при прохождении через каждую указанную точку, значит, они все являются точками перегиба.
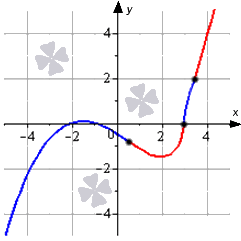
Ответ: Изобразим график функции, отметив вогнутости красным, выпуклости синим и точки перегиба – черным:
Зная первое достаточное условие перегиба, мы можем определить нужные точки, в которых не обязательно наличие второй производной. Исходя из этого, первое условие можно считать наиболее универсальным и пригодным для решения разных типов задач.
Отметим, что существует еще два условия перегиба, однако их можно применять только тогда, когда в указанной точке есть конечная производная.
Второе достаточное условие перегиба графика функции
Решение
Первое, что нужно сделать, – это убедиться в том, что данная точка вообще будет принадлежать графику этой функции.
Заданная функция определена для всех аргументов, являющихся действительными числами. Вычислим первую и вторую производные:
Третья производная не будет обращаться в нуль ни при одном значении x. Поэтому можно заключить, что данная точка будет точкой перегиба графика функции.
Ответ: Покажем решение на иллюстрации:
Третье достаточное условие перегиба графика функции
Решение
Теперь вычислим, при каких значениях вторая производная будет обращаться в 0 :
Мы получили, что при x = 3 график функции может иметь точку перегиба. Используем третье условие, чтобы подтвердить это:
Ответ: Вот график данной функции с отмеченными выпуклостями, вогнутостями и точкой перегиба:
Выпуклость графика функции.
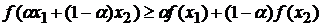
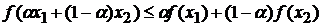
Выясним геометрический смысл этих неравенств. Рассмотрим точки 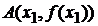
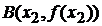
SHAPE \* MERGEFORMAT

















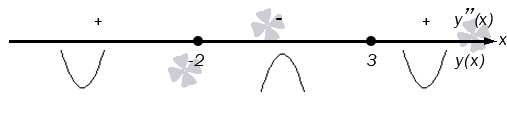
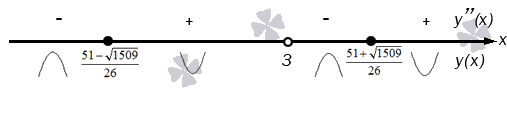
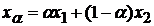 ,
, 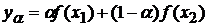 , где
, где 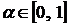 .
.
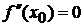 .
.