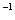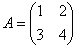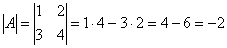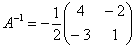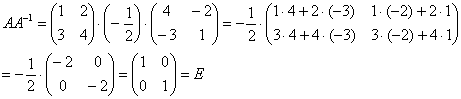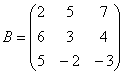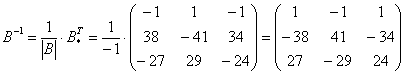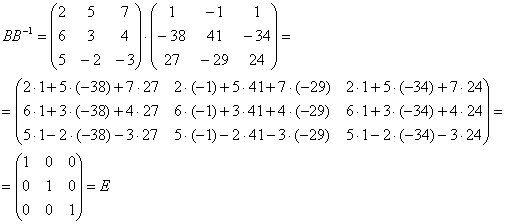какая матрица является обратной к e

Какая матрица является обратной к e

4.1 ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ

.

Легко показать, что

.

Рангом матрицы А (обозначается rang А или r ( A )) является наибольший порядок порожденных ею миноров (определителей), отличных от нуля. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется ее базисным минором. Строки и столбцы, участвующие в образовании базисного минора, также будут базисными. Матрица может иметь несколько базисных миноров, однако все их порядки одинаковы и равны рангу матрицы.

Ранг матрицы не изменится, если:

1) строки и столбцы матрицы поменять местами;

2) переставить местами два любых ее столбца (строки);

3) удалить из нее столбец (строку), все элементы которого равны нулю;

4) удалить из нее столбец (строку), являющийся линейной комбинацией остальных ее столбцов (строк);

5) умножить ее произвольный столбец (строку) на любое отличное от нуля число;

6) к любому ее столбцу (строке) прибавить произвольную линейную комбинацию остальных столбцов (строк) этой матрицы.

Преобразования 2) ‑ 6) называются элементарными. Две матрицы являются эквивалентными, если одна получается из другой с помощью элементарных преобразований и обозначается как А

Для рангов матриц справедливы следующие соотношения:

1) r (A + В ) r(A) + r(B),

3) r (A В ) min<r(A); r(B)>,

5) r ( A В ) = r ( A ), если В – квадратная матрица и D ( В ) 0,

Источник

Как найти обратную матрицу?

Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже если с математикой туго.

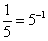
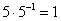
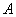
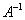
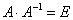
Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.

Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.

Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.

Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.

Сегодня мы изучим первый, более простой способ.

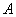
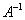
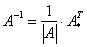
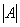
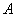
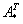
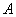
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

Найти обратную матрицу для матрицы

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.

Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

В рассматриваемом примере, как выяснилось, , а значит, всё в порядке.

2) Находим матрицу миноров .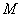

Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

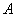
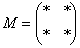
Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице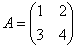
Сначала рассмотрим левый верхний элемент: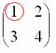

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: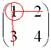

Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: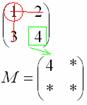

Рассматриваем следующий элемент матрицы :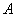

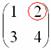
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: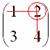

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: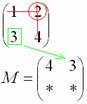

Аналогично рассматриваем элементы второй строки и находим их миноры: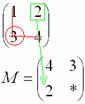


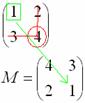
Готово.

– матрица миноров соответствующих элементов матрицы .

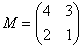
3) Находим матрицу алгебраических дополнений .

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: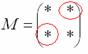

Именно у этих чисел, которые я обвел в кружок!

– матрица алгебраических дополнений соответствующих элементов матрицы .

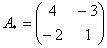
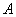
4) Находим транспонированную матрицу алгебраических дополнений .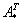

Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

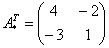
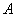
5) Ответ.

Вспоминаем нашу формулу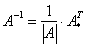
Всё найдено!

Таким образом, обратная матрица:

Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.

Как проверить решение?

Необходимо выполнить матричное умножение 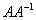либо

Проверка:

Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.

Таким образом, обратная матрица найдена правильно.

Если провести действие 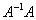, то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.

Переходим к более распространенному на практике случаю – матрице «три на три»:

Найти обратную матрицу для матрицы

Алгоритм точно такой же, как и для случая «два на два».

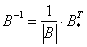
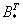
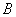
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

1) Находим определитель матрицы.

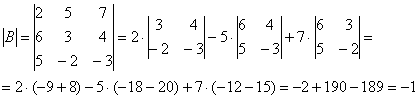
Здесь определитель раскрыт по первой строке.

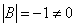
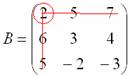
Также не забываем, что , а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров .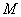

Матрица миноров имеет размерность «три на три» 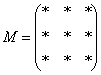, и нам нужно найти девять чисел.

Я подробно рассмотрю парочку миноров:

Рассмотрим следующий элемент матрицы: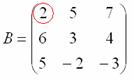

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшиеся четыре числа записываем в определитель «два на два»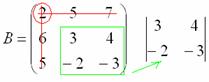

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: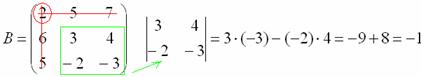

Всё, минор найден, записываем его в нашу матрицу миноров:

Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.

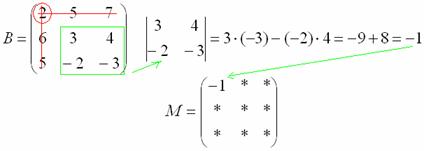
Ну и для закрепления – нахождение еще одного минора в картинках: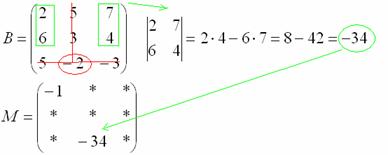

Остальные миноры попробуйте вычислить самостоятельно.

Окончательный результат:
– матрица миноров соответствующих элементов матрицы .

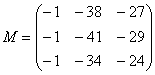
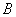
То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений .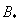

В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: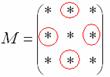

В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .

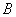
4) Находим транспонированную матрицу алгебраических дополнений .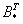

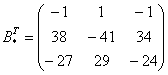
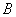
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

5) Ответ:

Проверка:

Таким образом, обратная матрица найдена правильно.

Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на странице Правило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.

Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).

В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.

Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник

Обратная матрица

Содержание

Обратимость в алгебре [ править ]

[math]xz=e, \ x[/math] — левый обратный

[math]zy=e, \ y[/math] — правый обратный.

Факт 2. Пусть [math]\exists z^<-1>, \ \tilde^<-1>[/math]

Критерий обратимости матрицы [ править ]

Предположим [math]\exists C: CA=E \Rightarrow \sum\limits_^ \gamma_^\alpha_^=\delta_^[/math]

Свойства обратной матрицы [ править ]

Методы нахождения обратной матрицы [ править ]

Метод Гаусса для нахождения обратной матрицы [ править ]

Пример [ править ]

Найдем обратную матрицу для матрицы

Метод присоединенной матрицы [ править ]

Алгебраическим дополнением элемента [math]\ a_[/math] матрицы [math]\ A[/math] называется число

[math]M_ = det\begin a_ <11>& a_ <12>& \cdots & a_ <1(j-1)>& a_ <1(j+1)>& \cdots & a_ <1n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ <(i-1)1>& a_ <(i-1)2>& \cdots & a_ <(i-1)(j-1)>& a_ <(i-1)(j+1)>& \cdots & a_ <(i-1)n>\\ a_ <(i+1)1>& a_ <(i+1)2>& \cdots & a_ <(i+1)(j-1)>& a_ <(i+1)(j+1)>& \cdots & a_ <(i+1)n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ & a_ & \cdots & a_ \\ \end[/math]

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Обратная матрица

Способы построения

Пример. Вычислить

Алгоритм обращения матрицы посредством приписыванием к ней единичной

2. Элементарными преобразованиями строк расширенной матрицы, добиваемся, чтобы в левой ее половине получилась единичная матрица.

Пример. Вычислить

$$ \left( \begin 4& 5 &1 \\ 1 & 3 &-2 \\ 3 & 1 & 2 \end \right)^ <-1>$$ приписыванием единичной матрицы.

Алгоритм шифрования Rijndael, используемый в мобильной телефонии, имеет в одной из стадий следующее преобразование байтов

$$ \begin y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \\ y_7 \end = \begin 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end \begin x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \end + \begin 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \end \pmod <2>$$ Найти обратное преобразование.

Ответ ☞ ЗДЕСЬ.

Свойства операции обращения

Если в левой части каждого каждого из следующих равенств операции определены, то равенства справедливы:

Использование для решения систем линейных уравнений

Обратные к конкретным типам матриц

1. треугольной матрице (верхней или нижней), если существует, то будет треугольной матрицей (того же типа);

2. симметричной матрице, если существует, то будет симметричной матрицей;

3. кососимметричной матрице нечетного порядка не существует, а в случае четного порядка, если существует, то будет кососимметричной матрицей;

В некоторых приложениях важно по виду матрицы быстро определить существует ли у нее обратная — без непосредственного нахождения этой обратной. Для некоторых типов матриц можно получить «вычислительно дешевые» критерии отличия их определителей от нуля.

Следующая теорема основана на связи определителя матрицы с ее собственными числами.

$$ |a_|>|a_|+\dots+|a_|+|a_|+\dots+|a_| \quad npu \quad \forall j\in \ <1,\dots,n\>$$ (модуль элемента на главной диагонали больше суммы модулей остальных элементов строки) называется матрицей с диагональным доминированием (преобладанием). Такая матрица всегда обратима.

Обращение блочных матриц

Найти обратную матрицу для матрицы Фробениуса

$$ <\mathfrak F>= \left( \begin 0 & 1 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & 0 & 1 & \dots & 0 & 0 \\ \dots& &&&\ddots & & \dots \\ 0 & 0 & 0 & 0 & \dots & 0 & 1 \\ a_n & a_ & a_ & & \dots & a_2 & a_1 \end \right)_ $$

Решение и ответ ☞ ЗДЕСЬ

Обращение «возмущенных» матриц

Следующий результат формулируем только для случая вещественных матриц, хотя существует его обобщение для комплексных.

Теорема [Шерман, Моррисон]. [3]. Пусть матрицы

Используется в модифицированном симплекс-методе, в котором на каждом шаге требуется вычислять обратную матрицу для матрицы, которая отличается от матрицы, полученной на предыдущем шаге только в одном столбце [4].

Псевдообратная матрица

Источники

[1]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960, с.187-192

[2]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

[3]. Gill P.E., Murray W., Wright M.H. Numerical Linear Algebra and Optimization. V.1. Addison-Wesley, NY, 1991

[4]. Таха Х. Введение в исследование операций. Т.1, глава 7. М.Мир. 1985

Источник