Парадоксы Зенона вводили в недоумение многих ученых и философов до 17 века. И до сих пор многие ученые спорят о бесконечности, структуре пространства и времени, хотя началось все с нескольких парадоксальных утверждений, ставящих поначалу в логический тупик любого умного человека.

История возникновения парадоксов Зенона

Зенон Элейский – философ Древней Эллады, ученик основателя Элейской школы – Парменида. Жил он с 515 по 450 год до нашей эры, о его жизни известно очень мало. Родился в городе Элее в южной части Италии. По утверждению Платона, Зенон побывал в Афинах и встретился с Сократом. Прославился благодаря своим апориям, в виде которых был сформулирован знаменитый парадокс Зенона. Апории Зенона представляют собой парадоксальные рассуждения, само же слово «апория» с греческого языка обозначает «безвыходность».

Парадоксы о движении и времени

Проблема решилась после идеи дифференциального исчисления, которую предложили Ньютон и Лейбниц. Там есть понятие «предел», так прояснилась разница между разбиением времени и разбиением на отрезки определенного пути. К тому же загадка разрешилась, когда ученые научились пользоваться бесконечно малыми величинами. Апории Зенона породили с тех пор множество различных вариаций. Кроме того, возможно, добавились некоторые детали. Мы перечислим сохранившиеся до наших дней парадоксы Зенона и кратко расскажем об их сути. Во всяком случае, попытаемся это сделать.

Парадокс Зенона об Ахиллесе и черепахе

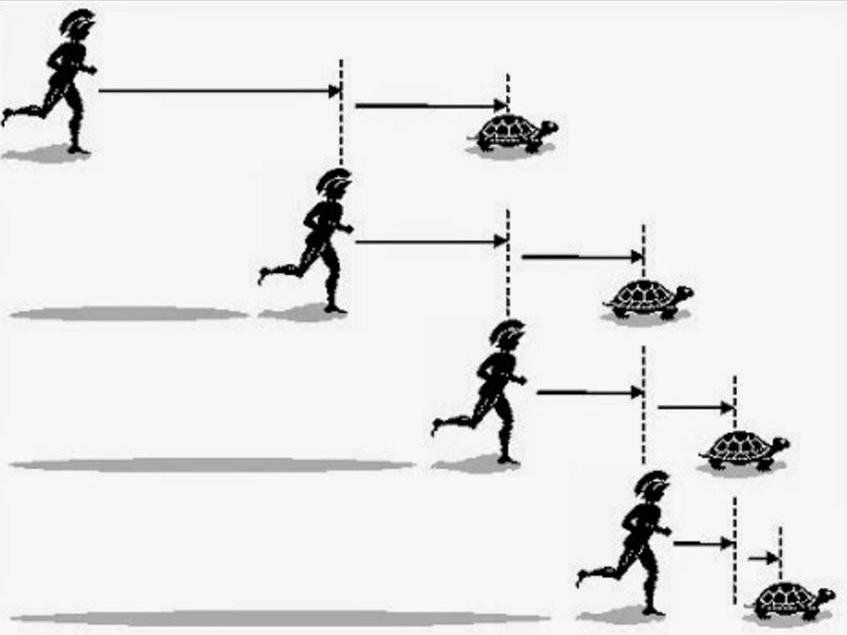
Герой мифов Древней Греции Ахиллес соревнуется в скорости бега с черепахой. Условия таковы, что черепаха стартует немного дальше, Ахиллес находится от нее на расстоянии в 1000 шагов.

Чтобы догнать черепаху, Ахиллес должен достигнуть сначала места, с которого черепаха стартовала. Но как только он добежит до этого места, черепаха успеет проползти 100 шагов. Это расстояние, которое она проползла, еще предстоит преодолеть Ахиллесу, но к тому времени она уползет еще дальше на 10 шагов и так далее. Число таких отрезков, которые нужно преодолеть Ахиллесу, по утверждению Зенона, может быть бесконечным, ведь величина этих отрезков все время будет уменьшаться до бесконечно малых величин.

Выходит, если следовать такой логике, древнегреческий герой никогда не догонит черепаху. Парадокс Зенона заключается в существовании бесконечного количества бесконечно малых отрезков, но в реальной жизни бегун наверняка обгонит медлительное животное.

Летящая стрела

Этот парадокс получил название «Стрела». Это еще одна апория, которую Зенон сформулировал приблизительно следующими словами. Если что-либо пребывает в движении, то оно движется либо в том месте, которое оно занимает собой, либо оно движется там, где его нет. Но оно не способно двигаться в том месте, которое оно занимает. Так как в каждую секунду оно занимает полностью все это место. Но и в том месте, где его нет, оно не может двигаться. Следовательно, движение само по себе невозможно.

По утверждению Зенона, стрела, когда летит, одновременно пребывает в покое. Потому что в каждый момент она занимает одно и то же пространство, равное ей. То есть стрела пребывает в покое относительно места, где она находится в определенный промежуток времени. Получается, что летящая стрела неподвижна. Если она неподвижна в определенный момент, значит, она находится в покое и в другие моменты времени. И нет того момента, когда стрела двигалась.

Дихотомия

Парадокс, который будет приведен далее, имеет название «дихотомия». В переводе с греческого языка оно означает «разделение надвое», и дано оно Аристотелем. Эта апория изложена примерно по такому же принципу, как и парадокс Зенона об Ахиллесе и черепахе.

В оригинале говорится о бегуне, который не в состоянии даже стартовать, ведь движения, по мнению Зенона, не существует. Но есть еще и распространенный вариант про пересечение комнаты.

Чтобы пересечь комнату, нужно сначала пересечь половину комнаты. На это уйдет определенная единица времени. После этого останется определенное расстояние, нужно преодолеть половину его за еще одну единицу времени. Затем тот отрезок пути, что остался, нужно разделить еще надвое и пройти половину этого отрезка за то же время. Тогда опять остается определенное расстояние, половину которого надо пересечь. Получается, что комнату пересекать можно бесконечно.

Две колонны на стадионе

Две колонны людей, одинаковые по длине, двигаются параллельно с одинаковой скоростью в противоположных направлениях. По утверждению Зенона, время которое истечет, когда колонны будут проходить мимо друг друга, равно половине того времени, которое нужно одному человеку, чтобы пройти мимо всей колонны.

Разрешение парадоксов Зенона

Из четырех перечисленных апорий наибольшую известность получили первые три. Четвертая появилась из-за неправильного понимания природы относительного движения.

Все апории можно легко опровергнуть экспериментально. Ничего не мешает пересечь комнату, выпустить стрелу и обогнать черепаху.

Рассмотрим парадокс, связанный с пересечением комнаты. Конечно, если разделить расстояние надвое и пройти половину, на это уйдет определенное количество времени. Останется еще расстояние, которое тоже нужно поделить надвое и пройти половину. Но для этого времени понадобится в два раза меньше. Чем меньше становится расстояние, которое необходимо преодолеть, тем больше будет сокращаться время на его прохождение. Выходит, при пересечении комнаты в конце требуется неограниченное число бесконечно маленьких временных отрезков. Но если сложить все отрезки, получится определенное число – оно-то и будет временем, затраченным на пересечение комнаты. Получается, пересечь комнату вполне возможно за определенный промежуток времени. Это доказательство схоже с нахождением предела при дифференциальном исчислении. Древнегреческий философ Зенон ошибочно предполагал, что при прохождении бесконечно малых расстояний каждый раз требуется одно и то же время.

Что касается парадокса Зенона «Летящая стрела», еще Аристотель его раскритиковал, утверждая, что каждый момент времени не может быть неделимым сам по себе. Еще он говорил, что рассуждения Зенона о том, что если все занимающее равное себе место пребывает в покое, и если то, что пребывает в движении, всегда занимает в любой момент такое же место, то стрела неподвижна, ошибочны.

Квантовый эффект

Парадоксы Зенона были опровергнуты со временем многими учеными. Но они все же внесли определенный вклад в науку. В квантовой физике на сегодняшний момент есть такое понятие, как квантовый парадокс Зенона. Он заключается в том, что если наблюдать за нестабильной частицей, например, проводить измерения, проверять, распалась частица или нет, то возникает некоторое замедление радиоактивного распада.

Предполагается, что если непрерывно наблюдать за частицей, то она может вообще не распасться. В 90-х годах прошлого века этот квантовый эффект был подтвержден с помощью ряда экспериментов.

Источник

Часть 15. Зенон.

частей сущего оказывается зараз и бесконечно малой и бесконечно великой. А именно, имея вне себя бесконечное множество всех прочих частей, она составляет бесконечно малую частицу всего; но, с другой стороны, слагаясь сама из бесконечного множества частиц, она представляет величину бесконечно великую. Примыкая отчасти к Вл. Соловьеву, кн. С. Трубецкой дает следующую остроумную реконструкцию первой антиномии. Если вещей много, то они вместе бесконечно малы и бесконечно велики. «Всякая вещь состоит из частей, всякая часть из других частей, и так далее до бесконечности. При этом каждая часть отдалена чем-то «сущим» от других». Какие же следствия вытекают отсюда? Во-первых, вещей бесконечное множество (так как сущее делимо до бесконечности), и, во-вторых, каждая вещь занимает бесконечное пространство (вследствие бесконечности своих частей). Каждая вещь (как и любая часть ее) оказывается бесконечно великой по протяжению, сущее же, как совокупность всех вещей, будет бесконечным множеством бесконечно больших пространственных величин. С другой стороны, каждая частица бесконечно мала, так как она отделена от всякой другой частицы бесконечным множеством частиц. Если отделить ее от всех других частиц, то она сама вовсе не будет иметь частей и величины. II. Дейссен «исправляет» первую антиномию Зенона следующим образом. Тело, состоящее из множества частиц, было бы 1) бесконечно малым и 2) бесконечно большим. Оно было бы бесконечно малым, так как его можно делить до бесконечности: оказывается, что тело состоит из суммы бесконечно малых частиц; сумма же бесконечно малых частиц может дать лишь бесконечно малое. Тело было бы бесконечно большим, так как при

беспрерывном делении мы получим, наконец, бесконечно много частиц; если из последних мы станем слагать тело, то, сколько бы их мы ни взяли, всегда будет оставаться еще бесконечное множество их, таким образом, вследствие того, что число их неисчерпаемо, мы можем увеличивать тело до бесконечной величины, По Дейссену Зенон здесь изолирует моменты, которые неразрывно связаны между собой: возрастающую малость и возрастающее количество частей.

Переходим ко второй антиномии. Если допустить существование многих вещей, то окажется, что; 1) вещей конечное число (тезис) и 2) вещей бесконечное число (антитезис). Ход аргументации сводится к следующему. Тезис: Если существует множество вещей, то их столько, сколько есть, не больше и не меньше. Следовательно, они существуют в определенном (ограниченном) количестве. Антитезис: Если вещей много, то их должно быть бесконечное число. В самом деле, допустим существование только двух вещей. Между двумя вещами необходимо должна лежать какая-либо третья вещь, их разделяющая, между последней и первыми опять новые вещи, и так далее до бесконечности. В противном случае, две смежные вещи слились бы в единство, образовывали бы одну вещь (а не две). Таким образом, двух не существует без трех, трех без пяти, пяти без девяти и так далее до бесконечности (так как число разделяющих вещей оказывается равным бесконечному ряду 1, 2,4,8,16 и т. д)1.

1 Антитезис второй антиномии не точно излагает Л. Штрюмпель: «Чтобы быть множественным, сущее должно быть разложимым на части. Деление же идет в бесконечность. Однако в нашем антитезисе речь идет не о делимости сущего, а о раздельности вещей, которые сами по себе рассматриваются как целые единицы».

В первой и второй антиномии Зенон рассматривает понятия единицы, конечного количества и количественной бесконечности. Диалектика числа у Зенона дает следующие результаты: единица =нулю, нуль = бесконечности, конечное количество (два) = бесконечному, часть = целому. Таким образом, понятие числа противоречиво, его применение незакономерно с точки зрения разума, число должно быть отнесено к области мнения и иллюзии. О первой антиномии говорит Т. Гомперц1: «Предпосылки этой аргументации не так уж произвольны, как это кажется на первый взгляд. Первая часть доказательства опирается на предпосылку абсолютной единицы, вторая на предпосылку абсолютной множественности». Ошибку Зенона он видит в том, что Зенон относительные понятия единства и множественности считал понятиями абсолютными.

2 П. Таннери прямо понимает вторую антиномию геометрически (см. ниже В1).

нечному пространству. Таким образом, диалектика Зенона разрушает понятие пространства наравне с понятием числа. В этом опять мы видим софистический момент его аргументов. “Основные идеи элейцев, понятия единства, протяженности”, реальности, сами были поколеблены или, лучше сказать, разрушены этой критикой, — справедливо говорит Т. Гомперц (стр. 179) об аргументах Зенона.

Против пространства Зенон дает и специальное доказательство. Все существующее находится где-нибудь, то есть в пространстве. А если так, то и само пространство, чтобы существовать, тоже должно находиться где-нибудь, т. е. в другом пространстве. Это второе пространство в свою очередь должно находиться в третьем пространстве, третье в четвертом и так далее. Таким образом, получим пространство пространства и т. д. до бесконечности. Следовательно, приходится или признать бесконечное число пространств, заключенных одно в другом, или же совсем отрицать существование пространства. В. Виндельбанд и Дж. Кернет находят в этом доказательстве отрицание лишь пустого пространства, а не пространственного бытия вообще. Действительно, приведенный аргумент отвергает только существование пространства, как чего-то отличного от заключенной в нем материи, между тем Парменид отожествлял материю и пространство. Однако этот аргумент легко может быть обращен и против элейской точки зрения с тем лишь различием, что в этом случае вместе с пространством будет отвергнуто и существование материи1.

Как аргумент против пространства, так и аргумент против истинности чувственного восприя-

1 Возражения против этого доказательства Аристотеля и Эвдема мы приводим ниже в переводе (См. А 21).

тия implicite заключают в себе опровержение множественности вещей. Аргумент против реальности чувственного восприятия известен под названием «пшенного зерна». В беседе с Протагором Зенон указывает, что между тем, как ни одно целое зерно, ни одна десятитысячная часть зерна при падении не издают звука, медимн пшена, падая, производит шум. Так кажется нам согласно свидетельству внешних чувств; однако разум требует, чтобы мы приняли что-либо одно: или и одно зерно и одна десятитысячная часть зерна при падении тоже издают звук, или и медимн пшена не производит шума. Ведь, в противном случае, мы получим, что сумма нулей равна не нулю, а некоторой положительной величине1.

М. Мандес исправляет аргумент «пшенного зерна», делая его иллюстрацией первой антиномии. Он излагает его следующим образом. Если любая часть зерна звучит, то совокупность звуков, производимых медимном зерна, будет бесконечно великой; если же ни зерно, ни десятитысячная часть зерна не звучат, то не будет звучать и медимн.

Аргумент «пшенного зерна» опровергает Аристотель в «Физике»2, говоря, это одно зерно не в состоянии привести в движение того количества воздуха, которое приводится в движение падением целого медимна пшена.

Наибольшей известностью пользовались всегда Зеноновы доказательства против движения, которых до нас дошло пять:1) доказательство общего характера, 2) «дихотомия», 3)»Ахиллес», 4) «стрела» и 5) «стадий». Первое доказательство против дви-

1. Таким образом, по способу аргументации это доказательство напоминает тезис первой антиномии.

жения1 весьма кратко: «Движущийся предмет не движется ни в том месте, где он находится, ни в том, где его нет». На вопрос, где происходит движение, должно ответить: нигде, так как тело не может двигаться там, где его нет; с другой стороны, занимая всегда пространство, равное своему объему, оно не может двигаться в этом месте, но покоится в нем.

Сущность доказательства, известного под названием «дихотомии», сводится к признанию невозможности движения на том основании, что движущийся предмет, прежде чем достигнуть какого-либо места, должен предварительно пройти половину пути, половину половины и так далее до бесконечности. Невозможно пройти бесконечное в конечное время. Как указывает М. Мандес, аргументация здесь обрывается, далее можно продолжать двояко. В самом деле, доказательство в своей полной форме могло говорить или 1) что движение не может закончиться (никогда не будет достигнут конечный пункт, так как, сколько бы к нему ни приближаться, всегда будет какой-либо остаток: проходя последовательно половину пути половину оставшейся половины и т. д. до бесконечности, движущийся предмет будет последовательно отстоять от цели движения на

первоначального расстояния, но конечный пункт будет оставаться всегда недостижимым) или 2) движение не может начаться, так как предмет не может достигнуть никакого пункта, не пройдя предварительно бесконечного числа промежуточных мест (чтобы пройти весь путь, он должен сначала пройти половину его; чтобы пройти эту

Аристотель2 усматривает ошибку этого доказательства в смешении бесконечно делимого с бесконечно большим. И время, возражает он, тоже бесконечно делимо. Конечное, но бесконечно делимое пространство проходится в конечный бесконечно делимый промежуток времени. Доказательство, по мнению Аристотеля, построено на предпосылке невозможности в конечное время пройти бесконечное пространство, и Аристотель, не отвергая этой предпосылки, указывает лишь, что, хотя пространство бесконечно делимо в возможности, однако в действительности оно в каждом своем отрезке не состоит из бесконечного числа частей, с другой же стороны время столь же бесконечно делимо, как и пространство, так что бесконечная делимость времени покрывает собой бесконечную делимость пространства (в этом видит решение проблемы также Лейбниц). И в наше время многие считают критику Аристотеля справедливой и вместе с ним видят основную ошибку доказательства в отождествлении бесконечной делимости и бесконечной величины. Так, по поводу приведенного доказательства Т. Гомперц говорит, что бесконечная делимость и бесконечная величина — два совершенно различных по-

1 Е. Durhring (Кrit.Geschichte d.Philos., 1869, стр. 40—47) говорит, что «дихотомия» без всякого изменения могла бы быть использованной элеатами для доказательства несуществования времени: невозможен переход от одного момента времени к другому, их разделяет такая же пропасть, какая лежит между двумя точками пространства.

нятия: конечная величина может быть делимой до бесконечности; Зенон-де выдвигает проблему отношения бесконечного ряда к конечной величине. Также ф. Арним говорит, что Зенон смешивает количественную бесконечность с дистрибутивной. И П. Дейссен присоединяется к мнению Аристотеля.

Однако эта критика не затрагивает существа Зенонова доказательства. Последнее (как и ряд других его аргументов) покоится на невозможности представить себе законченной бесконечность. Пусть время и пространство одинаково бесконечно делимы: переход от одного пункта к другому делается через это вдвойне неосуществимым. Мы получаем бесконечное количество пространственных точек, с одной стороны, моментов времени, с другой. Но мысль не может представить себе законченность бесконечного: непонятно, как может быть осуществлено бесконечное число актов движения, как может быть последовательно быть занятым бесконечное число положений в пространстве, и как может, наконец, придти к концу бесконечное число моментов времени. Поэтому рассматриваемое нами доказательство Зенона скорее лишь упрощает условия реализации движения, выдвигая лишь один момент — бесконечную делимость пространства.

С другой точки зрения критикует возражение Аристотеля П. Бейль1, который называет это возражение «жалким»2, доказательство же Зенона считает вполне правильным. Он рассуждает следующим образом. Во всяком движении есть terminus

1 Р Вау1е.Dictionnaire. t. IV, стр. 1264 след.

2 Еще резче Е. Дюринг, который говорит, что возражение Аристотеля, не давая действительного опровержения, обнаруживает лишь недостаток надлежащего понимания аргументов Зенона.

а quo (отправной пункт) и (terminus ad quem (конечный пункт)). Эти два термина отдалены пространством, заключающим в себе бесконечное число частей. Итак, чтобы достигнуть конечного пункта, необходимо последовательно пройти бесконечное число мест. Их можно было бы пройти лишь в бесконечное число моментов времени. Однако сущность времени, в отличие от пространства, заключается в том, что никакие части его не могут сосуществовать. Между тем как фут материи бесконечно делим (и, следовательно, действительно содержит в себе бесконечное число частей), час времени (год, столетие и т. п.) конечен, так как, если бы в часе времени было бесконечное число частей, он никогда не мог бы ни начаться, ни окончиться1.

Софистический момент в этом доказательстве Зенона заключается в том, что тем же самым умозаключением опровергается и самая возможность бесконечного деления конечной величины. Невозможно, чтобы в конечном заключалось бесконечно-многое, — это положение, во имя которого признается недопустимым результат, есть, однако, предпосылка всего построения.

Наибольшей славой пользовался всегда третий аргумент против движения — «Ахиллес»2. Самое

1 Это рассуждение П. Бейля о природе времени повторяет В.Petronievics.Zenos Beweise gegen die Bewegung(Archiv f.Gesch.d.Philos.,XX Bd.,1907,cтр 58.) который рассматривает все Зеноновы аргументы против движения с точки зрения финитизма (отрицания бесконечной делимости пространства и времени) и предлагает доктрину дуалистического финитизма (время и пространство состоят из точек двоякого рода реальных, или наполненных, и ирреальных, или пустых).

2 Этот аргумент Диоген Лаэрций приписывает самому Пармениду (см. 18А 1). По поводу этого доказательства*

напомним, что и Лейбниц считал понятие более быстрого

быстрое никогда не нагонит самого медлительного. Быстроногий Ахиллес не может догнать черепахи, так как каждый раз, когда он достигает занимаемого ею места, черепаха успевает несколько подвинуться вперед. Таким образом, чтобы настичь черепаху, Ахиллесу необходимо занять бесконечное множество мест, которые занимала черепаха. По мнению Аристотеля, этот аргумент есть иная форма первого аргумента (различие он усматривает лишь в способе деления, которое в «Ахиллесе» не дихотомическое).

Э. Целлер различие их видит в том, что в первом аргументе конечный пункт остается неизменным, во втором же он подвижен. Большинство полагает, что «Ахиллес» основан на том же, что и «дихотомия»: оба эти аргумента доказывают, что, если есть движение, то движущейся предмет должен в конечное время овладеть бесконечным пространством. Так, Аристотель дает критику «Ахиллеса», тождественную с критикой «дихотомии»: Зенон-де смешивает бесконечную делимость с бесконечной величиной; бесконечная делимость времени покрывает собой бесконечную делимость пространства. И в новое время многие присоединяются к критике Аристотеля: так, Т. Гоббс, Дж. Ст. Милль1 и Дж. Льюис также видят ошибку Зенона в отожествлении бесконечной делимости с бесконечной величиной.

движения противоречивым. Вообще аргумент «Ахиллес» всегда привлекал к себе наибольшее внимание. С. Ruelle(L’argument d’Achille в Revue philology,1907) приводит комментарий к нему Феодора Метохита (XIV в.) и первое математическое решение проблемы, которое дал в XVII в. Григорий de Saint-Vincent.

1 Дж. Ст. Милль дважды возвращается к этому вопросу в “Системе Логики” (стр. 743—744, пер. В. Ивановского, 11 изд.) и в Examination of SWH’s philosophy (стр. 533).

Анализируя доказательство «Ахиллес» и вышеприведенный ответ на него, Ибервег1 находит, что и то, и другое логически несостоятельно, потому что оба они доказывают слишком мало в сравнении с тем, что хотят доказать. Что касается ответа на Зенонов аргумент, то недостаточно простой ссылки на параллелизм бесконечной делимости пространства и времени. Ведь Зенон мог бы ответить, что как раз в силу этого параллелизма Ахиллес не догонит черепахи ни в какое время и ни в каком месте. С другой стороны, и аргумент Зенона доказывает слишком мало: он доказывает только, что, если обе скорости относятся, как n : 1, то встреча не может произойти внутри следующего ряда частей времени и частей пути:

Между тем вместо: «внутри этого ряда» Зенон говорит: «никогда и нигде». Право на это Зенон имел бы только в том случае, если бы раньше он доказал, что сумма этого ряда бесконечна. Но этого доказать невозможно, так как ложно то, что требуется доказать. Напротив, с математическою точностью можно доказать противоположное, а именно, что сумма этого ряда — и при бесконечном продолжении его — не превысит определенной конечной

величины (именно )). О математической стороне вопроса мы выскажемся ниже, здесь же заметим, что Ибервег справедливо указывает на неудовлетворительность ходячего возражения на аргумент «Ахиллес», видящего в нем alter ego аргумента «дихотомии». На самом же деле, в отличие от «дихотомии» «Ахиллес» предполагает одинако-

во бесконечно делимыми как пространство, так и время1: он поднимает ту же проблему, но в более усложненном виде.

На это усложнение вопроса обращает внимание Шнейдер (стр. 625 ц. с.), который говорит, что, вводя два движущихся тела, Зенон хотел указать новую трудность. То, что движется беспрерывно, должно подвинуться и в самый малый промежуток времени. Ахиллесу нужно некоторое время, чтобы пройти расстояние, отделяющее его от черепахи, но, так как черепаха движется беспрерывно, то ему опять нужно будет некоторое время для преодоления нового расстояния, и так далее до бесконечности, так как вследствие безостановочного движения черепахи расстояние между ними никогда не станет нулем. Ахиллес смог бы настигнуть черепаху только в том случае, если бы ему удалось пробежать в бесконечно малый промежуток времени не бесконечно малое расстояние. Действительно, главная трудность аргумента «Ахиллес» заключается в непонятности, как возможно преодоление того бесконечно малого пространства, которое всегда будет отделять Ахиллеса и черепаху, и, как справедливо указывает Шнейдер, решение вопроса требует нарушения параллелизма бесконечно делимых пространства и времени: Ахиллес настигнет черепаху, если в бесконечно малый промежуток времени он пройдет не бесконечно малое расстояние. Но это противоречит нашему убеждению, что движение требует времени. Итак, остается выбор между безвременным движением и движением бесконечным.

1 Если бы время не было бесконечно делимым, то был бы положен предел движению черепахи; скорее в бесконечной делимости времени — суть аргумента «Ахиллес».

Четвертое доказательство против движения — «стрела» утверждает: Летящая стрела покоится1. В основе этого доказательства лежала предпосылка, что время есть сумма моментов, а пространство — сумма точек. Это доказательство могло иметь двоякую форму, смотря по тому, указывалось ли на то, что стрела постоянно находится в одном месте, или в одном моменте времени (первую форму с различными видоизменениями принимают Фемистий, Целлер, Шнейдер, Дильс, Ренувье, вторую

Первая форма. В каждом пункте пути летящая стрела занимает одно определенное место, равное своему объему. Двигаться же невозможно, если занимать равное себе место (ибо для движения предмет нуждается в пространстве, большем себя). Если же в каждом пункте пути тело находится в покое, то движение тела слагается исключительно из состояний покоя. Итак, ряд состояний покоя вместе образуют движение (сумма нескольких, так сказать, нулей движения дает некоторую положительную величину)3.

Вторая форма. Летящая стрела покоится, так как она всегда находится в одном каком-нибудь (настоящем каждый раз) моменте времени. Момент времени неделим, и потому в течение его

1 См. А 27. Этому аргументу посвятил статью В. П. Сватковский («Парадокс Зенона о летящей стреле» в Ж.М.Н. Пр. 1888, апрель), который прилагает к. своему исследованию синоптическую таблицу всех относящихся сюда текстов.

2 Форма доказательства, предложенная Брошаром, предпочтительнее, так как при ней текст Аристотеля остается неприкосновенным, между тем как общепринятая первая форма требует внесения в текст поправок.

5 Этот нелепый вывод устраняется, если вместе с Лейбницем считать покой лишь бесконечно малым движением.

стрела не может изменить своего положения: в противном случае, момент времени оказался бы разделенным соответственно двум положениям стрелы в этот момент. А так как время состоит только из отдельных моментов, то движущийся предмет всегда находится в покое.

Аристотель ошибку этого доказательства видит в допускаемой предпосылке, что время слагается из отдельных неделимых моментов, между тем как, на самом деле, время — величина непрерывная. Аристотелю возражает П. Бейль, который излагает аргумент Зенона следующим образом. Стрела зараз и покоится и движется: в каждый отдельный момент времени она покоится, в несколько же таких моментов она передвинулась. Следовательно, движение противоречиво. С одной стороны, тело не может одновременно находиться в двух местах; с другой стороны, две части времени не могут сосуществовать совместно. Вся сила Зенонова доказательства в правильном, по мнению Бейля, положении, что нет ни малейшей части времени, которая могла бы сосуществовать с другой его частью; отсюда-де следует, что время не может быть делимо до бесконечности, но оно слагается из неделимых моментов.

С иной, нежели Аристотель, точки зрения возражает Зенону Эвеллен. Если пустого пространства не существует, то элементарное движение должно сильно отличаться от видимого нами эмпирического движения. Движущееся тело не раньше уходит из одного пункта пространства и не затем прибывает в следующий пункт, но то и другое совершается одновременно безо всякого промежутка времени между ними. При переходе с одного места на другое «уйти отсюда», «прибыть туда» и «находиться там» суть лишь различные обозна-

чения абсолютно одного и того же факта, а не различных моментов его (поскольку, конечно, дело касается элементарного движения). Для состояния же покоя нужны, по крайней мере, два момента пребывания на одном месте.

Интересное решение проблемы предлагает Дюринг. Следует отличать математическую точку, не имеющую вовсе протяжения, от имеющей измерения точки (в несобственном смысле слова) пространства; равным образом необходимо отличать временную точку, как не имеющую вовсе длительности границу времени, от весьма малой частицы времени. Наконец, должно от понятий покоя и движения отличать нейтральное (индифферентное) состояние. Точка покоится, если она в течение некоторого времени находится на одном и том же месте. Покой есть длящееся пребывание на одном месте. Равным образом временная длительность является необходимой предпосылкой для понятия движения (так как при движении точка занимает различные места). Если же мы возьмем мгновенное состояние тела, т. е. состояние безвременное (без всякой длительности), то оно будет одинаковым как для движущейся, так и для покоящейся точки. Математической временной точке соответствует вполне определенная ситуация и конфигурация всех точек пространства, находятся ли они в состоянии покоя или движения (в этом доказательство Зенона правильно). Это нейтральное состояние имеет всякая точка во всякое время, но это не есть нечто третье наряду с состояниями покоя и движения, но оно находится над ними или в них. Ошибка Зенона в том, что он отождествляет это нейтральное состояние с покоем и считает его несовместимым с движением.

В. Сватковский считает неудовлетворительным обычное понимание аргумента «стрелы», по которому здесь речь идет о многих моментах времени: в каждый отдельный момента стрела находится неподвижно на равном себе месте, так как-де малейшее передвижение потребовало бы некоторого перемещения будущего в прошедшее (данного момента было бы уже недостаточно). По мнению В. Сватковскаго, Зенон здесь не становится на общепринятую точку зрения, но имеет в виду лишь единый безвременный миг, единое непрерывное настоящее элейской школы. Это настоящее есть всегда, и потому движущийся предмет всегда неподвижен. Однако, если согласиться с В.Сватковским, то аргумент Зенона не даст ничего нового в сравнении с тем отрицанием движения, которое находится в поэме Парменида.

Отметим еще понимание аргумента, предлагаемое Гегелем. Летящая стрела находится всегда в определенном «теперь» и «здесь». «Теперь», как таковое, равно себе; равно себе также «здесь», как таковое. Если же во всех «теперь» (и во всех «здесь») нет никакого различия, то летящая стрела находится в состоянии, чуждом различий, т. е. покоится.

Пятое возражение против движения — «стадий»1. С противоположных сторон движутся по

1 См. А 28. Приводим для ориентировки фигуры.-

Начало движения Конец движени

Против «стадия» Аристотель возражает, указывая на различие единицы измерения: один раз расстояние отмеривается на покоящемся пространстве, другой раз на движущемся. Во всяком случае, аргумент Зенона вскрывает относительность движения. Иначе представляется положение вещей, если смотреть на движение каждого тела в отдельности, и иначе, если наблюдать их движения вместе относительно друг друга. Затруднение, которое вскрывает Зенон, было бы избегнуто, если бы наряду с материей допустить существование пустого пространства и считать движение изменением места в этом абсолютном пространстве (дефиниция Ньютона): в этом случае величина пройденного расстояния не измерялась бы на

телах, мимо которых прошло движущееся тело. Однако Зенон мог считать существование пустого абсолютного пространства опровергнутым в данном им специальном аргументе против пространства1. Аргумент «стадий», по справедливому указанию Шнейдера, показывает противоречия чувственно воспринимаемого движения (в отличие от предшествующих, где доказывалась невозможность движения для мысли).

Однако «стадий» может доказывать невозможность движения и для мысли, если в основание его положить предпосылку прерывности времени и пространства, состоящих из неделимых единиц. Такое понимание «стадия» мы находим у Брошара, Ноэля и Таннери. Две равные серии точек (соприкасающихся, но не сливающихся) движутся с одинаковой скоростью навстречу друг другу проходя мимо третьей равной им неподвижной серии точек. Точки — абсолютные элементы пространства; момент — абсолютный элемент времени. Допустим, что движение совершилось в один момент. В одно и то же время крайние точки каждой из движущихся серий пройдут мимо всех точек другой движущейся серии и в то же время только мимо половины точек покоящейся серии. Но если при одной и той же скорости времена движения должны быть пропорциональны проходимым пространствам, то оказывается, что неделимый момент времени вдвое больше самого себя: он должен расшириться так, чтобы содержать в себе два элемента того же измерения. Таким образом, момент, предположенный неделимым, оказывается делимым.

По мнению Таннери, «стадий» имеет в виду противника, утверждающего, что «момент соответству-

1 См. В. Petronievics, ц. с., стр. 71.

ет не определенному положению стрелы, но переходу от каждого данного положения к следующему». Зенон возражает, что, если при переходе из одного положения в другое всегда проходит момент, а все моменты равны между собой, то не может быть двойной скорости. Однако пример «стадия» показывает, что необходимо или допустить существование двойной скорости или признать, что половина может быть равна целому Конечный результат: переход от точки к точке не может соответствовать моменту. Толкование «стадия» у Таннери интересно в том отношении, что оно доказывает несостоятельность данной Т. Гомперцрм критики «стрелы». А именно, последний возражает Зенону: «Постоянно движущееся тело занимает и в самую малейшую частицу времени не одну часть пространства — оно находится в постоянном передвижении от одной части пространства к другой».

Эвеллен открывает в примере «стадия» еще следующее противоречие между чувственным созерцанием и мышлением. Точка В1 нашего рисунка, находившаяся влево от точки С1, после движения очутилась вправо от нее. Так как движение совершилось в один неделимый момент, то, хотя при сравнении прежнего и нового положения этих точек видно, что произошло их перекрещивание, однако встреча их не могла произойти ни в какое время и ни в каком месте. Они прошли мимо друг друга, но для их встречи не оказывается места ни в пространстве, ни во времени.

Связь между четырьмя аргументами против движения устанавливают Ренувье1 и Брошар2. «Ди-

1 Renouvier.Logique, р. 67.

хотомия», «Ахиллес», «стрела» и «стадий» образуют следующую дилемму. Если время и пространство имеют части, то одно из двух: или эти части делимы до бесконечности, или они состоят из неделимых элементов. «Дихотомия» и «Ахиллес» исходят из предположения, что пространство и время делимы до бесконечности, и опровергают его выведением из него нелепых следствий; «стрела» и «стадий» исходят из предположения, что пространство и время состоят из неделимых элементов и равным образом доказывают несостоятельность этого предположения. Эти четыре аргумента образуют симметрическую систему: I и IV рассматривают движение в данных границах, II и III — без них; I и III ставят задачу осуществления движения для одного тела и находят, что даже начало движения невозможно, V и IV сравнивают два движущихся тела и доказывают, что, если бы даже движение началось, оно не могло бы продолжаться. I и II устанавливают невозможность движения вследствие природы пространства, которое предполагается непрерывным наравне с временем; в III и IV невозможность движения доказывается на основании природы времени, которое предполагается прерывным наравне с пространством. Наконец, второй аргумент покоится на том же принципе, что и первый; а четвертый — на одном принципе с третьим. Аргументы расположены в логическом порядке: наиболее простые раньше, более сложные за простейшими.

Также Дж. Вернет находит в каждом последующем аргументе усложнение предыдущего: в «Ахиллесе» усложнена «дихотомия» введением другого движущегося объекта; дальнейшее усложнение представляет стрела: движущийся предмет рассматривается, как имеющий длину; «стадий» — ус-

ложнение «стрелы»: вводится вторая движущаяс

Обратимся теперь к математической стороне вопросов, поднятых аргументами Зенона против движения. Б. Рессель переводит доказательства Зенона на язык арифметики. Дихотомия: нет движения так как движущийся предмет должен постоянно (бесконечное число раз) достигать половины своего пути, прежде чем достигнет конца На арифметическом языке это значит: числа от 0 до 1 предполагают числа от 0 до последние предполагают числа от 0 до и т. д. (бесконечный прогресс в понятии бесконечного целого). Решение проблемы Рессель находит в различении или двух видов бесконечного регресса, или двух видов целого, в одном из которых части одинаковой сложности с целым не имеют логического приоритета перед целым. Ахиллес: проблема, поднимаемая этим аргументом с арифметической точки зрения сводится к взаимному отношению двух бесконечных классов. Например возьмем 1+ 2х и 2 + х, и допустим, что х лежит между 0 и 1. Для каждого значения 1+ 2х есть одно и только одно значение 2 + х и vice versa. Когда х возрастет от 0 до 1, тогда оба эти значения сравняются. Однако 1 + 2х отправляется от 1 и кончается 3 между тем как 2+х начинается 2-мя и кончается 3. «Ахиллес» затрагивает и другую интересную математическую проблему, вопрос об равномош-

1 Проведение этой точки зрения у Таннери см.стр. 240-247 р. п. его основной работы

2 B. Russel.The principes of mathematics,v.I,1903 стр. 347 след.

ности (similarity) целого и части. Если здравый смысл (common-sence) не может допустить возможности того, чтобы целое и часть могли иметь одно и то же число терминов, то «Ахиллес» Зенона доказывает, что противоположная точка зрения также приводит к следствиям, неприемлемым для здравого смысла. Здравый смысл оказывается в весьма плачевном состоянии: ему приходится выбирать между парадоксом Зенона и парадоксом Кантора, между «Ахиллесом» и «Тристрамом Шен-ди» (Tristam Shandy)1. Трисграм Шенди потратил два года своей жизни на написание истории двух первых дней своей жизни и горевал, что при та-

момент, Рессель считает совершенно основательным с чисто арифметической точки зрения (пока не включается никакой эмпирический вопрос); но в геометрии, кинематике и динамике этот аргумент получает иную оценку.

По господствующему в исторической литературе мнению, аргументы Зенона были направлены против убеждения всех смертных в реальности движения и множественности вещей. Против этого мнения выступил П. Таннери, который полагает, что аргументы Зенона были направлены только против пифагорейцев. Парменидово учение об единстве, сплошности и неподвижности вселенной противоречило пифагорейскому учению, по которому точка есть единица пространства. Геометрическое тело, учили пифагорейцы, есть сумма точек (равным образом и физическое тело, так

как в то время еще не делали различия между геометрическим и физическим телами). Зенон дает этому пифагорейскому учению формулировку: «вещи суть множественность» и опровергает его. «Объясненные в этом смысле аргументы Зенона, даже те, в которых видят простые паралогизмы, являются ясными, убедительными и неопровержимыми», говорит Таннери.Мильо (Milhaud) и Боймкер, следуя Таннери, также видят в доказательствах Зенона критику пифагорейского учения, по которому тело состоит из точек, и с этой точки зрения признают ценность всех аргументов Зенона (они превосходно выполняют свое назначение, которым является опровержение пифагореизма). К этому мнению присоединяется и Т. Гомперц (стр. 177), который, отмечая возникший в пифагорейских кругах взгляд, что «делимости материи не преступить некоторой, хотя и очень отдаленной границы: дальнейшему бесконечному делению препятствуют мельчайшие зерна, которые по величине можно сравнить с концом иглы или с солнечной пылью», прибавляет: «Неоспоримая заслуга Зенона заключается в том, что он указал на противоречивость этого представления». Мнение Таннери разделяет также Дж. Вернет (стр. 362), который изображает историческую позицию Зенона следующим образом: сперва выступает Парменид, затем его противники пифагорейцы — плюралисты, утверждающие, что пространство (и тело) состоит из раздельных единиц, наконец, Зенон, дающий критику этого плюралистического учения. Против мнения Таннери, Мильо, Боймкера, Т. Гомперца и Дж. Бернета делает возражение Брошар (стр. 19ц. с.), обращающий внимание на то, что Платон1 проти-

вополагает элейское учение не пифагорейскому, но ионийским и сицилийским музам (т. е. Гераклиту и Эмпедоклу). И действительно, мы имеем идущее от древности сообщение, что Зенон написал сочинение, посвященное Эмпедоклу, которое, по мнению Г Дильса, должно было быть полемического содержания. Сверх того, бесконечная делимость пространства, задаваемая критикой Зенона, скорее всего может быть поставлена в связь с учением Анаксагора1. Наконец, высказывался взгляд, что аргументы Зенона были направлены против Левкиппа. Несомненно, что аргументы Зенона различными своими сторонами не могли не коснуться всех современных им учений и не могли не повлиять на последующие философские построения. Мы не видим необходимости ставить эти аргументы в исключительную связь с пифагорейским атомизмом2; как показывает уже самое число аргументов Зенона (до 50, из которых до нас дошло около 10, — вероятно, те, которые показались наиболее значительными Аристотелю и Симплицию), они должны были иметь в виду всех возможных противников не только существующих, но и мыслимых (согласно завещанию Парменида. см. 18 В 8,61). Мы полагаем, что аргументы Зенона, будучи все объединены одной целью — защитить учение Парменида, были направлены против различных противников этого учения: они

1 Взгляд Штальбаума. высказанный им в издании Платоновского “Парменида”, стр. 25 cл.

2 Генетической связи элеатизма с пифагореизмом, конечно, отрицать нельзя: сам Парменид первоначально был пифагорейцем и на элейскую школу в древности смотрели, как на ветвь пифагорейского союза (Страбон). В известном смысле элейская школа является сектой, отделившейся от пифагореизма. См. J.Burnet, стр. 358.

опровергали как обыденный взгляд на мир, основанный на показаниях внешних чувств, так и современные Зенону философские учения (в частности пифагорейский атомизм); сверх того, вероятно, Зенон в силу своего диалектического таланта сам строил мыслимые возражения, отыскивал воображаемых противников (может быть, таким путем им были предвосхищены предпосылки мировоззрений Анаксагора и Левкиппа).

Если по мнению Таннери, Зенон доказывал, «что тело не есть сумма точек, что время не есть сумма моментов, что движение не есть сумма простых переходов от точки к точке» (стр. 248), то по мнению Эвеллена, аргументы Зенона, напротив, доказывают несуществование непрерывных величин. Брошар полагает, что доказательства Зенона были направлены не против существования, но против состава непрерывной величины: существуют лишь непрерывные величины, но они — такого рода, что исключают всякую множественность; число для Зенона есть «чистая видимость и иллюзия» (pure apparence et illusion), оно должно быть изгнано из подлинной науки.

Однако, разрушая понятие числа (единства, множества, бесконечности), диалектика Зенона устремляется затем на основные геометрические понятия (пространство и точка) и далее на главные понятия физики (материя, время, движение, скорость), и повсюду эта диалектика действует разлагающим образом. Она разрушает понятие материи, доказывая, что материя не состоит ни из математических точек, ни из физических, ни из частей, делимых до бесконечности (несколько нулей пространства не составят пространства, следовательно, математические точки не образуют материи; делимость до бесконечности делает

часть равной целому; физические точки — атомы заключают в себе противоречие: с одной стороны, они имеют протяжение, а именно, верх и низ, правую и левую сторону и потому делимы до бесконечности, с другой стороны, ставится требование мыслить их неделимыми (то есть, в понятии атома мы должны мыслить неделимой делимую до бесконечности величину). То, во имя чего производит свою разрушительную работу диалектика Зенона, — непрерывная материя, чуждая какой бы то ни было множественности и потому исключающая всякую делимость, является понятием, которому приходится отказать в логической ясности. По мнению Таннери (стр.237), Зенон «вовсе не отрицал движения, но лишь доказывал несовместимость его со множественностью вещей». Однако знаменитое возражение циников на аргументы Зенона доказывает, что в древности эти аргументы понимались именно в смысле отрицания возможности движения вообще. Известно, что, выслушав аргументы Зенона против движения, Антисфен, не сказав ни слова, поднялся и стал, ходить (см. А 15). В сущности, возражение циников считает правильным П. Дейссен (ц. с., стр. 88 след.), так как он полагает, что аргументы Зенона покоятся на разногласии, существующем между мышлением и чувственным созерцанием. А именно, по мнению П. Дейссена, Зенон злоупотребляет мышлением в ущерб правам чувственного созерцания: действительность, данная нам в созерцании, непрерывна (continium), между тем как мышление разрывает эту действительность, проводя в последней чуж-дые ей границы; время и пространство — непрерывные величины, и только мышление делает их суммой отдельных моментов и точек; суть вопроса в том, что мышление является несовершенным

орудием для понимания действительности. Наилучшим опровержением взгляда П. Дейссена могут служить работы математика Г. Кантора, который показал, что понятие непрерывной величины может быть построено независимо от данных нам в чувственной интуиции времени и пространства что, отправляясь от понятия прерывной величины, можно при помощи чистой логической конструкции достигнуть понятия непрерывной величины1. Непрерывная величина не является чем-то недоступным нашему мышлению. Тем не менее, действительно, существует глубокое различие между математическим (абсолютно однородным) пространством и пространством психологическим (эмпирическим), но это различие иного рода и этот вопрос у Зенона еще не затронут2.

Общее историческое значение Зенона заключается в его громадном влиянии на развитие греческой математики3, в его критике понятия материи, которая подготовила позже возникший идеализм, и в его диалектическом методе, проло-

3 H.Hankel.Zur Geschichte d.Mathenatik 1874 стр. 117, M.Cantor.Vorlesungen uder Geschichte d.Mathematik,стр.168-170П. Таннери, р. п., стр. 236.

живщем путь позднейшей софистике1. Сам Зенон не был ни математиком, ни физиком-идеалистом, ни софистом, но он дал сильнейший толчок развитию основных математических и физических понятий, а также сильно способствовал возникновению идеалистического мировоззрения и софистических приемов (особенно его влияние сказалось на Горгии).

Свида (см. А 2) приписывает Зенону насколько сочинений: «Споры», «Изъяснение учений Эмпедокла» (не экзегетического, но полемического содержания, по мнению Г. Дильса), «Против философов»2 и «О природе». Диоген (см. А 14) говорит, будто Зенон первый стал писать диалоги. Полагая, что Зенон писал в диалогической форме, Таннери считает дошедшие до нас отрывки неподлинными (так как в них не сохранилось следа диалогической формы).

Аристотель написал специальное сочинение «Против учений Зенона»; посвятил также Зенону книгу Гераклид Понтийский.

Из философских систем нового времени любопытные параллели аргументам Зенона представляют, с одной стороны, космологические антиномии Канта (а именно, две первые, математические антиномии) и учение Ренувье об антиномической форме категорий3, с другой стороны, системы

1 В самом деле, та характеристика метода Зенона. которую дает Платон в «Федре» (Рhaedr.216 D, см. А13), может без всяких изменений служить выражением сущности метода софистов. Псевдо-Гален считает Зенона скептиком и эристикой. Также пирроновцы признавали Зенона скептиком (см. В 4).

2 Т. е. против пифагорейцев, по мнению Дж. Бернета.

Тренделенбурга и Бергсона, которые обе построены на принципе движения, но самое движение считают не поддающимся определению. Тренделенбург говорит, что «движение можно только созерцать и указывать, а отнюдь не истолковывать и не определять»1 и вследствие простоты движения считает ошибочными «все попытки поставить пространство и время независимо, как моменты, предшествующие движению и его обусловливающие». Пространство и время «выделяются и для представления только из движения, как из общего своего источника». Ошибку аргументов Зенона2 он видит в том, что в них нарушено данное в созерцании движения единство времени и пространства и они противопоставлены враждебно друг другу, как совсем чуждые между собой элементы. Бергсон дает остроумную критику аргументов Зенона против движения с точки зрения основных принципов своей философии. Сущность ошибки, допущенной в них, он видит в том, что делимость пути движения переносится на самое движение. Аргументы Зенона предполагают, что то, что верно относительно пути, верно и относительно самого движения. «Так, например, линия может быть подразделена на сколько угодно частей какой угодно величины, и все же это будет одна и та же линия. Отсюда делается вывод, что мы имеем право, когда угодно, расчленять движение, и все же это будет то же самое движение. Таким образом, получается ряд нелепостей, вытекающих из одной и той же основной нелепости. Когда Ахиллес гонится за черепахой, то каждый

1 А. Транделенбург. Логические исследования, I часть, стр. 137 р. П.

2 Там же, стр. 196—200.

его шаг должен рассматриваться как нечто нераздельное. То же самое относится и к шагу черепахи. Это совершенно очевидно. Если вы хотите далее подразделить оба эти движения, то различите в пути Ахилла и в пути черепахи меньше части шага каждого из них, но непременно считайтесь с естественным единством обоих путей. Прием Зенона состоит в том, что движения Ахилла составляются по другому; произвольно выбранному закону»1.

Итак, Бергсон видит общую ошибку всех аргументов Зенона в том, что «движение накладывается на свою траекторию и произвольно разлагается на части подобно ей». «В сущности, — говорит он, — ошибка объясняется тем, что однажды выполненное движение оставило на своем пути неподвижную траекторию, на которой можно насчитать сколько угодно неподвижных точек. А отсюда делается вывод, что и совершающееся движение в каждый момент оставляет за собой некоторое положение, с которым оно совпадало. При этом упускается из виду, что траектория создается одним ударом, хотя для этого, конечно, нужно известное время; что если однажды созданную траекторию можно подразделять на какие угодно части, то никак нельзя подразделять самый процесс ее создания, так как это именно — процесс, а не предмет. Предполагать же, что движущееся тело находится в какой-либо точке своего пути, это, значит разрезать путь на две части и заменить двумя траекториями ту единую траекторию, которая рассматривалась сначала. Это, значит, различать два последовательных акта там, где по предположению имеется только один. Наконец, это значит

1А. Бергсон. Творческая эволюция, II изд. р. п., стр. 276-277

переносить на самый полет стрелы все то, что относится к пройденному ею промежутку, то есть а priori допустить ту нелепость, что движение совпадает с неподвижными состояниями»1.

В заключение лишь упомянем о той роли, какую играет проблема отношения между непрерывным и прерывным в мировоззрении Г. Геффдинга (в гносеологической, психологической, космологической и этически-религиозной областях)2.

1.Диоген IX 25 след. (25). Элеец Зенон. Аполлодор в «Хрониках» говорит, что он — родной сын Телевтагора, усыновленный Парменидом (Парменид же — сын Пирета). О нем и Мелисс Тимон говорит следующее:

«Великая, неистощимая сила двуязычного Зенона, порицателя всех, и Мелисс возвышаются над многими призраками и только немногим (из них) подчиняются».

Итак, Зенон был учеником Парменида и предметом его любви. Он был высокого роста, как говорит Платон в «Пармениде» (127В; срв.Л 11). Он же в «Софисте» (р. 215 А) [и в «Федре» он упоминает его (р. 261 D)] называет его элейским Паламедом. Аристотель же (fr.. 65; срв. А 10) говорит, что он был изобретателем диалектики, подобно тому как Эмпедокл — риторики.

2 Геффдинг. Философские проблемы.

(2 7) Димитрий же в «Омонимах» говорит, что он откусил (царю) нос. Антисфен же в «Сменах» говорит, что после того как он указал друзей, тиран спросил, нет ли еще кого-нибудь, он же сказал: «Ты — государственный преступник», и, обратившись к присутствовавшим, промолвил: «Удивляюсь я вашей трусости, если вы служите тирану из страха подвергнуться тому, что я ныне терплю», и, наконец, откусив (свой) язык, выплюнул его (в лицо) тирану, поощренные же (этим поступком) граждане тотчас побили тирана камнями. Почти то же самое болтает большинство (авторов). Гермипп же говорит, что он был брошен в ступу и изрублен на мелкие части (срв. 59 А 13).

(28) И на него мы сказали так (Следует эпиграмма Диогена). И в остальных отношениях Зенон был хорош, но притом он, подобно Гераклиту презирал (все) более значительное. И в самом деле, свой родной город, бывший фокейской колонией, называвшийся сначала Гиэлой, а позже Элеей, го-

род ничтожный, умевший лишь воспитывать хороших мужей, он предпочитал надменным Афинам. Он ни разу не бывал у афинян, но жил на родине. (29) Он первый выступил с рассуждением, которое называется Ахиллесом. Впрочем, Фаворин говорит (ср. выше стр. 21), что Парменид и многие другие (раньше его).

Мнения же его таковы1. Существуют миры и нет пустоты. Природа всех (вещей) произошла из теплого, холодного, сухого и влажного, когда они стали переходить одно в другое. Люди произошли из земли; душа есть смесь из вышеупомянутых (элементов) такого рода, что ни один из них не преобладает. Передают, что, когда его бранили, он обнаружил недовольство; когда же кто-то поставил ему это в вину, он сказал: «Если брань меня не тронет, то и похвал я не почувствую».

О том, что было восемь (известных) лиц, носивших имя Зенона, об этом мы сказали, когда говорили о Зеноне Китайском (VII 35). Акме нашего Зенона) пришлось на (семьдесят) девятую олимпиаду (464—461).

2. Сеида. Зенон, сын Телевтагора, элейский философ из числа близких по времени к Пифагору и Демокриту, ибо он жил в 78 олимпиаду (468 — 465), ученик Ксенофана или Парменида. Он написал (следующие сочинения): «Споры», «Изъяснение учений Эмпедокла»2, «Против философов», «О природе» (из Гезихия).

1 Приводимые далее мнения принадлежат, вероятно, Эмпедоклу: к последнему относится и приводимое здесь изречение, как видно из 21 А 20. Если эти мнения действительно принадлежали Зенону. то они свидетельствуют, что Зенон так же, как Парменид, счел нужным дать и «мнимое учение» ().

2 Сочинение полемического содержания.

3. Евсевий Сbrоп. к олимпиаде 81, 1—3 (456— 454). Было акме Зенона и Гераклита Темного. Срв. 18А11и29A1а.

Схолии к этому месту. Элеец Зенон, ученик Парменида, философ, занимавшийся исследованием природы, и государственный муж в подлинном смысле этого слова. Поэтому-то он и сравнивается с Периклом, мнимым государственным мужем. Его слышал Пифодор, который удостоен упоминания также в «Пармениде» в качестве лица, сообщившего Антифону содержание известной беседы; у него-то научившись стал Кефал Клазоменский учителем (других).

Плутарх Реricl 4,3. Перикл слушал также элейца Зенона, занимавшегося, подобно Пармениду, изучением природы и выработавшего (в себе) некоторую способность опровергать (противника) и посредством возражений ставить его в затруднительное положение. Срв. 18 А 12.

5. Аристотель Rbet. А 12. 1372 b 3 И, напротив, те, для которых несправедливые поступки в некотором роде похвальны, оставляются без защиты, как, например, если вместе с тем пришлось отомстить за отца или мать, подобно Зенону.

б.Диодор X18,2. Когда отечество подпало под жестокую тиранию Неарха, он составил заговор против тирана. Когда он был уличен и Неарх под пыткой допрашивал его, кто были соучастниками

7- Плутарх аdv.. Со1о1.32 р. 1126 D. Итак, Зенон, приятель Парменида, устроив покушение на тирана Демила и потерпев неудачу в (этом) деле, показал учение Парменида, как бы чистое и неподдельное золото в огне, и доказал на деле, что великому мужу постыдно быть трусливым, страданий же боятся дети, женщины и имеющие женские души мужчины. Дело в том, что, откусив себе язык, он выплюнул его в лицо тирану.

8. Климент Strot. IV57. Не только эсопии, македоняне и лакедемоняне, будучи подвергаемы

9.Филострат V.Ароll. Туап, VII2. Итак, элеец Зенон (кажется, он положил начало диалектике), пытаясь уничтожить тиранию) Неарха Мизийского1, был схвачен и, будучи подвергнут пытке, не выдал своих соучастников, по наговорил на тех, которые были верны тирану, будто они ему неверны. Последние были казнены, как будто в самом деле были виновны. Он же (таким образом) сделал мизян свободными, ниспровергнув тиранию в лицо ее приверженцев.

10.Диоген VIII57 (срв.А 1). Аристотель же в «Софисте» говорит, что Эмпедокл первый изобрел риторику, Зенон же диалектику

Секст adv.matb.тсйЪ. VII6. По-видимому, Парменид был весьма сведущ в диалектике, так как тот же Аристотель признал начинателем диалектики его приятеля Зенона.

11.ПлатанРагт. 137АВ. Итак, Антифон сказал, что Пифодор рассказывал, как некогда пришли на великие панафинеи Зенон и Парменид. И вот Парменид был уже совершенно седым, настоящим стариком, обладал прекрасной и благообразной наружностью и имел, самое большее, около 65 лет от роду Зенону же было в то время приблизитель-

1 Очевидно, смешение Элей с Элайей.

но сорок лет; он был высокого роста и приятной наружности. И о нем говорили, будто он был предметом любви Парменида. Они остановились, сказал (Антифон), у Пифодора за городской стеной в Керамике. Итак, туда пришел Сократ и с ним много других (лиц) с намерением послушать сочинений Зенона. Дело в том, что последние тогда впервые были принесены ими. Сократ же в то время был весьма юн. Читал им сам Зенон, Парменида же в то время не было дома. И уже из рассуждений, которые читались, очень немного оставалось (дочитать), как вошли в дом, сказал Пифодор, сам он и с ним Парменид и Аристотель, ставший (позже) одним из тридцати (тиранов) и кое-что немногое из сочинения еще услышали и т.д. Срв. стр. 32. Напротив Атеней 505f. Но что всего ужаснее и всего лживее, это — сказать без всякой настоятельной надобности, будто предметом любви Парменида был согражданин его Зенон.

12. Платон Рarт. 128В. «Да, Сократ», сказал Зенон: «однако, истинный смысл сочинения ты понял не совсем, хотя, подобно лакедемонским щенкам, отлично преследуешь и отыскиваешь по следам (содержание) изложенного. Но, во-первых, от твоего внимания ускользнуло то обстоятельство, что (мое) сочинение вовсе не так уж превозносит себя, чтобы оно могло быть написано с тою целью, какую ты ему приписываешь, (а именно), чтобы, утаивая от людей (свое истинное значение, делало вид), будто производит нечто великое. А (то, что) ты привел в качестве одного из следствий (сочинения), это именно и есть истинная цель этого сочинения, (а именно), оно есть своего рода защита учения Парменида против пытающихся осмеивать его (и утверждающих), что, если (принять положение, что) существует единое, то учению

Источник