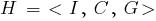какая модель представления знаний использует выражения вида если условие то действие
Классификация моделей представления знаний
В настоящее время разработано множество моделей представления знаний. Имея обобщенное название, они различаются по идеям, лежащим в их основе, с точки зрения математической обоснованности. Рассмотрим классификацию на рисунке.
Рис 1. Классификация моделей представления знаний.
Первый подход, называемый эмпирическим, основан на изучении принципов организации человеческой памяти и моделировании механизмов решения задач человеком. На основе этого подхода в настоящее время разработаны и получили наибольшую известность следующие модели:
1)продукционные модели – модель, основанная на правилах, позволяет представить знание в виде предложений типа: «ЕСЛИ условие, ТО действие». Продукционная модель обладает тем недостатком, что при накоплении достаточно большого числа (порядка нескольких сотен) продукций они начинают противоречить друг другу. Также к ее недостаткам можно отнести неясность взаимных отношений правил и сложность оценки базы знаний.
Рост противоречивости продукционной модели может быть ограничен путём введения механизмов исключений и возвратов. Механизм исключений означает, что вводятся специальные правила-исключения. Их отличает большая конкретность в сравнении с обобщёнными правилами. При наличии исключения основное правило не применяется. Механизм возвратов же означает, что логический вывод может продолжаться в том случае, если на каком-то этапе вывод привёл к противоречию. Просто необходимо отказаться от одного из принятых ранее утверждений и осуществить возврат к предыдущему состоянию.
Существуют два типа продукционных систем – с «прямыми» и «обратными» выводами. Прямые выводы реализуют стратегию «от фактов к заключениям». При обратных выводах выдвигаются гипотезы вероятностных заключений, которые могут быть подтверждены или опровергнуты на основании фактов, поступающих в рабочую память. Существуют также системы с двунаправленными выводами.
В общем случае продукционную модель можно представить в следующем виде:
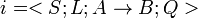
S–Описание класса ситуаций;
L–Условие, при котором продукция активизируется;
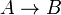
Q– Постусловие продукционного правила;
«двигатель не заводится»
«стартёр двигателя не работает»
«неполадки в системе электропитания стартёра»
2)сетевые модели (или семантические сети) – информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Формально сеть можно задать в следующем виде:
I – множество информационных единиц;
C – Множество типов связей между информационными единицами;
G– Отображение, задающее конкретные отношения из имеющихся типов междуэлементами.
В семантической сети роль вершин выполняют понятия базы знаний, а дуги (причем направленные) задают отношения между ними. Таким образом, семантическая сеть отражает семантику предметной области в виде понятий и отношений.
Как правило, различают экстенсиональные и интенсиональные семантические сети. Экстенсиональная семантическая сеть описывает конкретные отношения данной ситуации. Интенсиональная – имена классов объектов, а не индивидуальные имена объектов. Связи в интенсиональной сети отражают те отношения, которые всегда присущи объектам данного класса.
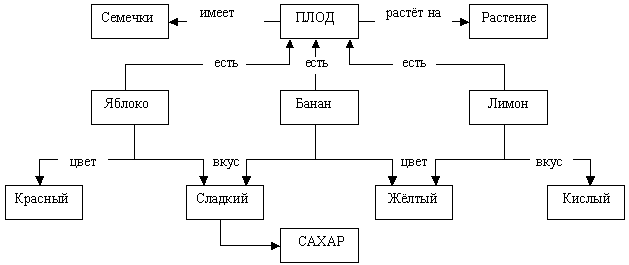
Примеры семантической сети:
Рис 2. Пример семантической сети.
Рис 3. Семантическая сеть, упорядоченная отношениями «целое — часть», «род — вид».
3) фреймовая модель – основывается на таком понятии как фрейм (англ. frame – рамка, каркас). Фрейм – структура данных для представления некоторого концептуального объекта. Информация, относящаяся к фрейму, содержится в составляющих его слотах. Слот может быть терминальным (листом иерархии) или представлять собой фрейм нижнего уровня.
Фреймы подразделяются на:
Ø фрейм-экземпляр – конкретная реализация фрейма, описывающая текущее состояние в предметной области;
Ø фрейм-образец – шаблон для описания объектов или допустимых ситуаций предметной области;
Ø фрейм-класс – фрейм верхнего уровня для представления совокупности фреймов образцов.
Пример фреймовой модели:
Рис 4. Структура фреймовой модели.
4) ленемы представляют собой смешанный тип модели, являющийся как бы «развитием» других моделей (фреймы, семантические сети и т.д.). Ленема предназначена для структурного комплексного описания понятий предметной области. По изобразительным возможностям ленемы более совершенны, чем такие традиционные модели представления знаний, как семантическая сеть, фрейм, система продукций. Однако, для некоторых понятий, модель представления знаний, на основе ленем, может быть неудобной и даже неприемлемой. Например, это такие понятия, в описании которых очень большую роль играет внутренняя динамика. Модель, созданная на базе ленем, позволяет объединить на пользовательском уровне три существующие в настоящее время парадигмы представления знаний:
1) логическую (продукционная и логическая модели);
2) структурную (семантические сети и фреймы);
Для некоторых ситуаций это очень удобно, так как при реализации сложных моде-лей, включающих знания различных типов, возникает необходимость совмещения в одном языке представления знаний различных концепций.
5)Нейронные сети, генетические алгоритмы. Эти модели нельзя строго отнести к эмпирическому или теоретическому подходам. Их относят, как было сказано ранее, к бионическому направлению. Оно основывается на предположении о том, что если в искусственной системе воспроизвести структуры и процессы человеческого мозга, то и результаты решения задач такой системой будут подобны результатам, получаемым человеком.
6) Логическая модель. Вся информация в логической модели рассматривается как совокупность фактов и связывающих их утверждений, которые представляются как формулы в некоторой логике. Знания при этом представляются набором подобных утверждений, а построение выводов и получение новых знаний сводится к реализации процедуры логического вывода. Этот процесс может быть строго формализован, так как в его основе лежит классический аппарат математической логики.
Для представления математического знания в математической логике пользуются логическими формализмами — исчислением высказываний и исчислением предикатов. Эти формализмы имеют ясную формальную семантику и для них разработаны механизмы вывода. Поэтому исчисление предикатов было первым логическим языком, который применяли для формального описания предметных областей, связанных с решением прикладных задач.
Логическиемоделипредставления знаний реализуются средствами логики предикатов.Предикат – логическая N-арная пропозициональная функция, определенная для предметной области и принимающая значения либо истинности, либо ложности.
Пример логической модели:
ДАТЬ (МИХАИЛ, ВЛАДИМИРУ, КНИГУ);
Здесь описаны два способа записи одного факта: «Михаил дал книгу Владимиру».
Логический вывод осуществляется с помощью силлогизма (если из A следует B, а из B следует C, то из A следует C).
7)Комбинаторные модели основаны на рассмотрении дискретных объектов, конечных множеств и заданном на них отношении порядка. В рамках комбинаторики также рассматриваются все возможные изменения, перестановки и сочетания, в рамках заданных множеств.Под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Комбинаторные модели используются в задачах топологии (например, поиск пути), задачах прогнозирования поведения автоматов, при изучении деревьев решений, частично упорядоченных множеств.
Основная проблема указана еще в определении этой модели: она оперирует только дискретными объектами и конечными множествами, связанными однородными отношениями.
8) Алгебраическая модель подразумевает представление знаний в виде некоторых алгебраических примитивов, над которыми определено множество действий (некоторые из которых можно задать таблично). Для набора знаний представленного в таком виде действуют правила алгебраических множеств, такие как формализация, определение подсистем и отношений эквивалентности. Также возможно построение цепей множеств (множества, для которых определен порядок отношения «быть подсистемой»).
Изначально предполагалось использовать подобную модель в качестве формализованной системы построения аналогий (за счет определения эквивалентности). Однако, на эту формальную модель очень сложно отобразить весь набор знаний, поэтому от этой идеи отказались.
Второй подход можно определить как теоретически обоснованный, гарантирующий правильность решений. Он в основном представлен моделями, основанными на формальной логике (исчисление высказываний, исчисление предикатов), формальных грамматиках, комбинаторными моделями, в частности моделями конечных проективных геометрий, теории графов, тензорными и алгебраическими моделями. В рамках этого подхода до настоящего времени удавалось решать только сравнительно простые задачи из узкой предметной области.
Заключение
На сегодняшний день разработано уже достаточное количество моделей. Каждая из них обладает своими плюсами и минусами, и поэтому для каждой конкретной задачи необходимо выбрать именно свою модель. От этого будет зависеть не столько эффективность выполнения поставленной задачи, сколько возможность ее решения вообще.
Список используемой литературы
1. Гаврилова Т. А., Хорошевский В. Ф. Базы знаний интеллектуальных систем. Учебник. — СПб.: Питер, 2000.
2. Дьяконов В.П., Борисов А.В. Основы искусственного интеллекта.—Смоленск, 2007.
Модели представления знаний
Физико-математические науки
Похожие материалы
Информация, с которой имеют дело ЭВМ, разделяется на процедурную и декларативную. Процедурная информация овеществлена в программах, которые выполняются в процессе решения задач, декларативная – в данных с которыми эти программы работают. Стандартной формой представления информации в ЭВМ является машинное слово, состоящее из определенного для данного типа ЭВМ числа двоичных разрядов – битов. Однако в ряде случаев машинные слова разбиваются на группы по восемь двоичных разрядов которые называются байтами.
Параллельно с развитием структуры ЭВМ происходило развитие информационных структур для представления данных. Появились способы описания данных в виде векторов и матриц, возникли списочные структуры, иерархические структуры. В настоящее время в языках программирования высокого уровня используются абстрактные типы данных, структура которых задается программистом. Появление баз данных (БД) знаменовало собой еще один шаг на пути организации работы с декларативной информацией. В базах данных могут одновременно хранится большие обьемы информации, а специальные средства образующие систему управления базами данных (СУБД), позволяют эффективно манипулировать с данными, по необходимости извлекать их из базы данных и записывать их в нужном порядке в базу.
По мере развития исследований в области ИС возникла концепция знаний, которая объединила в себе многие черты процедурной и декларативной информации.
Представление знаний – это одно из направлений в исследованиях по искусственному интеллекту. Другие направления это – манипулирование знаниями, общение, восприятие, обучение и поведение.
Особенности знаний
Существует ряд особенностей, присущих различным формам представления знаний в ЭВМ.
Внутренняя интерпретируемость
Каждая информационная единица должна иметь уникальное имя, по которому ИС находит её, а также отвечает на запросы, в которых это имя упомянуто. Когда данные, хранящиеся в памяти, были лишены имен, то отсутствовала возможность их идентификации системой. Данные могла идентифицировать лишь программа, извлекающая их из памяти по указанию программиста, написавшего программу. Что скрывается за тем или иным двоичным кодом машинного слова, системе было неизвестно.
Структурированность
Информационные единицы должны были обладать гибкой структурой. Для них должен выполняться “принцип матрешки”, т.е. рекурсивная вложенность одних информационных единиц в другие. Каждая информационная единица может быть включена в состав любой другой, и из каждой единицы можно выделить некоторые её составляющие. Другими словами должна существовать возможность произвольного установления между отдельными информационными единицами отношений типа “часть – целое”,” род – вид” или “элемент – класс”.
Связность
Перечисленные три особенности знаний позволяют ввести общую модель представления знаний, которую можно назвать семантической сетью, представляющей собой иерархическую сеть в вершинах которой находятся информационные единицы.
Семантическая метрика
На множестве информационных единиц в некоторых случаях полезно задавать отношение, характеризующее информационную близость информационных единиц, т.е. силу ассоциативной связи между информационными единицами. Его можно было бы назвать отношением релевантности для информационных единиц. Такое отношение дает возможность выделять в информационной базе некоторые типовые ситуации (например «покупка», «регулирование движения»). Отношение релевантности при работе с информационными единицами позволяет находить знания близкие к уже найденным.
Активность
С момента появления ЭВМ и разделения используемых в ней информационных единиц на данные и команды создалась ситуация, при которой данные пассивны, а команды активны. Все процессы, протекающие в ЭВМ, инициируются командами, а данные используются этими командами лишь в случае необходимости. Для ИС эта ситуация неприемлема. Как и у человека, в ИС актуализации тех или иных действий способствуют знания, имеющиеся в системе. Таким образом, выполнение программ в ИС должно инициироваться текущим состоянием информационной базы. Появление в базе фактов или описание событий, установление связей может стать источником активности системы.
Перечисленные пять особенностей информационных единиц определяют ту грань, за которой данные превращаются в знания, а базы данных перерастают в базы знаний (БЗ). Совокупность средств, обеспечивающих работу со знаниями, образуют систему управления базой знаний (СУБЗ). В настоящее время не существует баз знаний, в которых в полной мере были бы реализованы перечисленные выше особенности [1].
Модели представления знаний
Во многих случаях для принятия решений в той или иной области человеческой деятельности неизвестен алгоритм решения, т.е. отсутствует четкая последовательность действий, заведомо приводящих к необходимому результату. Например:
При принятии решения в таких случаях необходимо иметь некоторую сумму знаний о самой этой области. Например: при выборе наилучшего хода в конкретной шахматной позиции необходимы знания о правилах игры, силе шахматных фигур, стратегии и тактике и многое другое. Под знаниями понимается то, что стало известно после изучения. Совокупность знаний, нужных для принятия решений, принято называть предметной областью или знаниями о предметной области.
В любой предметной области есть свои понятия и связи между ними, своя терминология, свои законы, связывающие между собой объекты данных предметной области, свои процессы и события. Кроме того, каждая предметная область имеет свои методы решения задач.
Решая задачи такого вида на ЭВМ используют ИС, ядром которых являются базы знаний, содержащие основные характеристики предметных областей [2].
При построении баз знаний традиционные языки, основанные на численном представлении данных, являются неэффективными. Для этого используются специальные языки представления знаний, основанные на символьном представлении данных. Они делятся на типы по формальным моделям представления знаний. Различные авторы по-разному эти модели классифицируют. Основные модели знаний представлены на рисунке 1.
Рисунок 1. Основные модели знаний
Продукционная модель знаний
Продукционные модели можно считать наиболее распространенными моделями представления знаний. Продукционная модель – это модель, основанная на правилах, позволяющая представить знание в виде предложений типа:
«ЕСЛИ условие, ТО действие»
Продукционная модель обладает тем недостатком, что при накоплении достаточно большого числа (порядка нескольких сотен) продукций они начинают противоречить друг другу.
Системы обработки знаний, использующие продукционную модель получили название «продукционных систем». В состав экспертных систем продукционного типа входят база правил (знаний), рабочая память и интерпретатор правил (решатель), реализующий определенный механизм логического вывода. Любое продукционное правило, содержащееся в базе знаний, состоит из двух частей: антецендента и консеквента. Антецедент представляет собой посылку правила (условную часть) и состоит из элементарных предложений, соединенных логическими связками «и», «или». Консеквент (заключение) включает одно или несколько предложений, которые выражают либо некоторый факт, либо указание на определенное действие, подлежащее исполнению. Продукционные правила принято записывать в виде антецедент-консеквент.
Примеры продукционных правил:
ЕСЛИ «двигатель не заводится» И «стартер двигателя не работает»
ТО «неполадки в системе электропитания стартера»
Основные достоинства систем, основанных на продукционных моделях:
К недостаткам таких систем можно отнести следующее:
При разработке небольших систем (десятки правил) проявляются в основном положительные стороны продукционных моделей знаний, однако при увеличении объёма знаний более заметными становятся слабые стороны.
Логическая модель знаний
Основная идея при построении логических моделей знаний заключается в следующем – вся информация, необходимая для решения прикладных задач, рассматривается как совокупность фактов и утверждений, которые представляются как формулы в некоторой логике. Знания отображаются совокупностью таких формул, а получение новых знаний сводится к реализации процедур логического вывода.
Основные достоинства логических моделей знаний:
В логических моделях знаний слова, описывающие сущности предметной области, называются термами (константы, переменные, функции), а слова, описывающие отношения сущностей – предикатами.
Предикат – логическая N-арная пропозициональная функция, определенная для предметной области и принимающая значения либо истинности, либо ложности. Пропозициональной называется функция, которая ставит в соответствие объектам из области определения одно из истинностных значений («истина», «ложь»). Предикат принимает значения «истина» или «ложь» в зависимости от значений входящих в него термов [3].
Способ описания предметной области, используемый в логических моделях знаний, приводит к потере некоторых нюансов, свойственных естественному восприятию человека, и поэтому снижает описательную возможность таких моделей.
Сложности возникают при описании «многосортных» миров, когда объекты не являются однородными. Так, высказывания:
«Москва – столица России»
имеют одно и то же значение «истина», но разный смысл. С целью преодоления сложностей и расширения описательных возможностей логических моделей знаний разрабатываются псевдофизические логики, т.е. логики, оперирующие с нечеткостями, обеспечивающие индуктивные (от частного к общему), дедуктивные (от общего к частному) и традуктивные (на одном уровне общности) выводы. Такие расширенные модели, объединяющие возможности логического и лингвистического подходов, принято называть логико-лингвистическими моделями предметной области.
Сетевая модель знаний
Однозначное определение семантической сети (сетевой модели знаний) в настоящее время отсутствует. В инженерии знаний под ней подразумевается граф, отображающий смысл целостного образа. Узлы графа соответствуют понятиям и объектам, а дуги – отношениям между объектами.
Семантическая сеть как модель наиболее часто используется для представления декларативных знаний. С помощью этой модели реализуются такие свойства системы знаний, как интерпретируемость и связность. За счет этих свойств семантическая сеть позволяет снизить объем хранимых данных, обеспечивает вывод умозаключений по ассоциативным связям.
Одной из первых известных моделей, основанных на семантической сети, является TLC-модель (Teachaple Languge Comprehender – доступный механизм понимания языка), разработанная в 1968 году. Модель использовалась для представления семантических отношений между концептами (словами) с целью описания структуры долговременной памяти человека в психологии.
Как правило, различают экстенсиональные и интенсиональные семантические сети. Экстенсиональная семантическая сеть описывает конкретные отношения данной ситуации. Интенсиональная – имена классов объектов, а не индивидуальные имена объектов. Связи в интенсиональной сети отражают те отношения, которые всегда присущи объектам данного класса.
Фреймовая модель знаний
Фреймовая модель основана на концепции Марвина Мински (Marvin Minsky) – профессора Массачусетского технологического института, основателя лаборатории искусственного интеллекта, автора ряда фундаментальных работ. Фреймовая модель представляет собой систематизированную психологическую модель памяти человека и его сознания.
Фрейм – это минимально возможное описание сущности какого-либо события, ситуации, процесса или объекта. Существует и другое понимание фрейма – это ассоциативный список атрибутов. Понятие «минимально возможное» означает, что при дальнейшем упрощении описания теряется его полнота, и оно перестает определять ту единицу знаний, для которой было предназначено. Представление знаний с помощью фреймов понимается как один из способов представления знаний о ситуациях. Фрейм имеет имя (название) и состоит из слотов.
Слоты – это незаполненные (нулевые) позиции фрейма. Если у фрейма все слоты заполнены – это описание конкретной ситуации. В переводе с английского слово «фрейм» означает «рамка», а слово «слот» – «щель». В отличие от моделей других типов во фреймовых моделях фиксируется жесткая структура информационных единиц, которая называется протофреймом. В общем виде структура информационных единиц выглядит следующим образом:
Значением слота может быть практически что угодно (числа, математические соотношения, тексты на естественном языке или на языке программ, ссылки на другие слоты данного фрейма). Значением слота может выступать и отдельный фрейм, что является очень удобным для упорядочивания знаний по степени общности. Исключение из фрейма любого слота делает его неполным, а иногда и бессмысленным.
При конкретизации фрейма ему и слотам приписываются конкретные имена и происходит заполнение слотов. Таким образом из протофреймов получаются фреймы – экземпляры. Переход от исходного протофрейма к фрейму – экземпляру может быть многошаговым, за счет постепенного уточнения значений слотов [4].
Рассмотрим некоторый протофрейм:
Фамилия (значение слота1);
Год рождения (значение слота2);
Специальность (значение слота3);
Стаж (значение слота4)).
Если в качестве значений слотов использовать конкретные данные, то получим фрейм – экземпляр:
Фамилия (Попов – Сидоров – Иванов – Петров);
Год рождения (1965 – 1975 – 1980 – 1978);
Специальность (директор – бухгалтер – техник – курьер);
Стаж (15 – 7 – 3 – 4)).
Связи между фреймами задаются значениями специального слота с именем «связь».
Фреймы подразделяются на:
Заключение
Модели представления знаний – это одно из важнейших направлений исследований в области искусственного интеллекта. Без знаний искусственный интеллект не может существовать. Действительно, представьте себе человека, который абсолютно ничего не знает. Например, он не знает даже таких элементарных вещей как:
Таких примеров удастся привести еще много, но уже сейчас можно легко ответить на следующий вопрос: «Поведение такого человека может считаться разумным?». Конечно же, нет. Именно поэтому, при создании систем искусственного интеллекта особенное внимание уделяется моделям представления знаний.
На сегодняшний день разработано уже достаточное количество моделей. Каждая из них обладает своими плюсами и минусами, и поэтому для каждой конкретной задачи необходимо выбрать именно свою модель. От этого будет зависит не столько эффективность выполнения поставленной задачи, сколько возможность ее решения вообще.
Список литературы
Завершение формирования электронного архива по направлению «Науки о Земле и энергетика»
Создание электронного архива по направлению «Науки о Земле и энергетика»
Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.
Соучредители СМИ: Долганов А.А., Майоров Е.В.