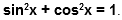какая окружность называется единичной
Единичная окружность
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Для чего использовать единичную окружность
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
1. Конспект для учителя по теме «Числовая окружность»
Что такое числовая окружность? Для чего она нужна?
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность.
Для успешной работы с единичной окружностью нужно знать всего три вещи.
Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику.
Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность.
Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.
Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.
Угол в 1

В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти:
Какая окружность называется единичной
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно “не очень. ”
И для тех, кто “очень даже. ” )
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику. Сходите по ссылке, кто ещё не был. Тогда и здесь всё ясно будет.
Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность. Это я расскажу прямо здесь и сейчас.
Всё. Разобравшись с этими тремя китами, получим надёжную, безотказную и совершенно законную шпаргалку для всей тригонометрии сразу.
А то в школьных учебниках с этим самым тригонометрическим кругом как-то не очень… И с единичной окружностью. Да и с числовой окружностью тоже.)
В предыдущем уроке вы усвоили, что синус, косинус, тангенс и котангенс (т.е. тригонометрические функции) зависят только от угла. И не зависят от длин сторон в прямоугольном треугольнике. Отсюда интересный вопрос. Пусть у нас есть вот такой угол. Назовём его угол β. Буква красивая.)
Раз есть угол, у него должны быть тригонометрические функции! Синус, скажем, или котангенс… А где их взять? Нет ни гипотенузы, ни катетов…
Как определить тригонометрические функции угла без прямоугольного треугольника? Задачка… Придётся опять лезть в сокровищницу мировых знаний. К средневековым людям. Те всё умели.
Первым делом возьмём координатную плоскость. Это самые обычные координатные оси, ОХ – по горизонтали, ОY – по вертикали. И… прибьём одну сторону угла к положительной полуоси ОХ. Вершина угла, естественно, в точке О. Крепко прибьём, чтобы не оторвать! Вторую сторону оставим подвижной, чтобы угол менять можно было. Раздвижной у нас угол будет. Конец неприбитой стороны угла обозначим точкой А. Получим вот такую картинку:
Так, угол пристроили. А где его синус, где косинус? Спокойно! Сейчас всё будет.
Так вот, число В будет косинусом угла β, а число С – его синусом!
С чего бы это? Древние люди учили нас, что синус и косинус – это отношения сторон! Которые от длин сторон не зависят. А мы тут координаты точки придумали… Но! Посмотрите на треугольник ОАВ. Прямоугольный, кстати… По древнему определению косинус угла β равен отношению прилежащего катета к гипотенузе. Т.е. ОВ/ОА. Ладно, не возражаем. Причём косинус и синус не зависят от длин сторон. А это вообще отлично! Это значит, что длины сторон можно брать какие угодно. Имеем полное право взять длину ОА за единицу! Неважно чего. Хоть метр, хоть километр, всё равно синус/косинус не меняются. А в этом случае
Вот так. Если провести такие же рассуждения для синуса, получим, что синус угла β равен АВ. Но АБ = ОС. Следовательно,
Можно сказать совсем просто. Синусом угла β будет игрековая координата точки А, а косинусом – иксовая. Слова нестандартные, но тем лучше. Запоминается надёжнее! А запомнить это надо. Железно запомнить. Косинус – по иксу, синус – по игреку.
Нет, не обидели средневековые люди древних! Сберегли наследие! И отношение сторон сохранили, и возможности расширили чрезвычайно!
Однако, а где тригонометрический круг!? Где единичная окружность!? Где числовая окружность!? Ни слова про круги не было!
Верно. Но осталось всего ничего. Взять подвижную сторону ОА и повернуть её вокруг точки О на полный оборот. Как вы думаете, какую фигуру нарисует при этом точка А? Совершенно верно! Окружность! Вот она.
Вот это и будет тригонометрический круг.
Вспомнив, что ОА = 1, а ОА – радиус, сообразим, что это же – и единичная окружность тоже.
Три термина в одном флаконе.)
В данной теме эти понятия: тригонометрический круг, единичная окружность и числовая окружность – одно и то же. В более широком смысле, единичная окружность – это любая окружность с радиусом, равным единице. Тригонометрический круг – практический термин, как раз для работы с единичной окружностью в тригонометрии. Чем мы сейчас и позанимаемся. Работой с тригонометрическим кругом.
Первую половину работы мы уже выполнили. Нарисовали числовую окружность с помощью угла (классно звучит, правда?).
Теперь выполним вторую половину работы. Сделаем то же самое, только наоборот. Пройдём путь от тригонометрического круга к углу.
Всё понятно? Внимание, вопрос!
Где β!? Где угол β, без которого синуса и косинуса не бывает!?
Наводим курсор на картинку, и. вот он, вот он угол β! Именно его синус и косинус являются координатами точки А.
Кстати, здесь не нарисована прибитая сторона угла. Она и в предыдущих рисунках не нужна, только так, для понимания. Угол всегда отсчитывается от положительного направления оси ОХ. От направления стрелки.
Самые наблюдательные заметят, что синус угла β – положительный (точка С – на положительной полуоси OY), а вот косинус – отрицательный! Точка В лежит на отрицательной полуоси ОХ.
Наводим курсор на картинку и видим угол β. Угол β здесь – тупой. Чего, кстати, решительно не бывет в прямоугольном треугольнике. А зря, что ли, мы возможности расширяли?
Уловили суть тригонометрического круга? Если взять точку в любом месте окружности, её координатами будут косинус и синус угла. Угол отсчитывается от положительного направления оси ОХ и до прямой, соединяющей центр координат с этой самой точкой на окружности.
Вот и всё. Проще хотелось бы, да некуда. Кстати, мой вам совет. Работая с кругом, рисуйте не только точки на единичной окружности, но и сам угол! Как на этих рисунках. Понятнее будет.
И нигде-то вы подсказку не найдёте. Только на числовой окружности. Рисуем примерный угол в правильной четверти и сразу видим, куда попадают его синус и косинус. На положительные полуоси, или отрицательные. Кстати, определение знаков тригонометрических функций постоянно требуется в самых различных заданиях.
Долго? Да ну?! Никто не требует от вас тщательно прорисовывать картину и обеспечивать мультипликацию! Поработаете с этим сайтом, и по этой задаче будете за 10 секунд рисовать вот такую картинку:
Другой и не сообразит, что это за каракули, да… А вы спокойно и уверенно дадите правильный ответ! Хотя, аккуратность и не мешает. А то можно такую “окружность” нарисовать, что ответ обратный получится.
Подведём итоги урока.
В этой теме мы плавно перешли от тригонометрических функций угла в прямоугольном треугольнике к тригонометрическим функциям любого угла. Для этого нам понадобилось освоить понятия “тригонометрический круг, единичная окружность, числовая окружность”. Это очень полезно.)
Далее мы разберёмся со следующими вопросами.
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
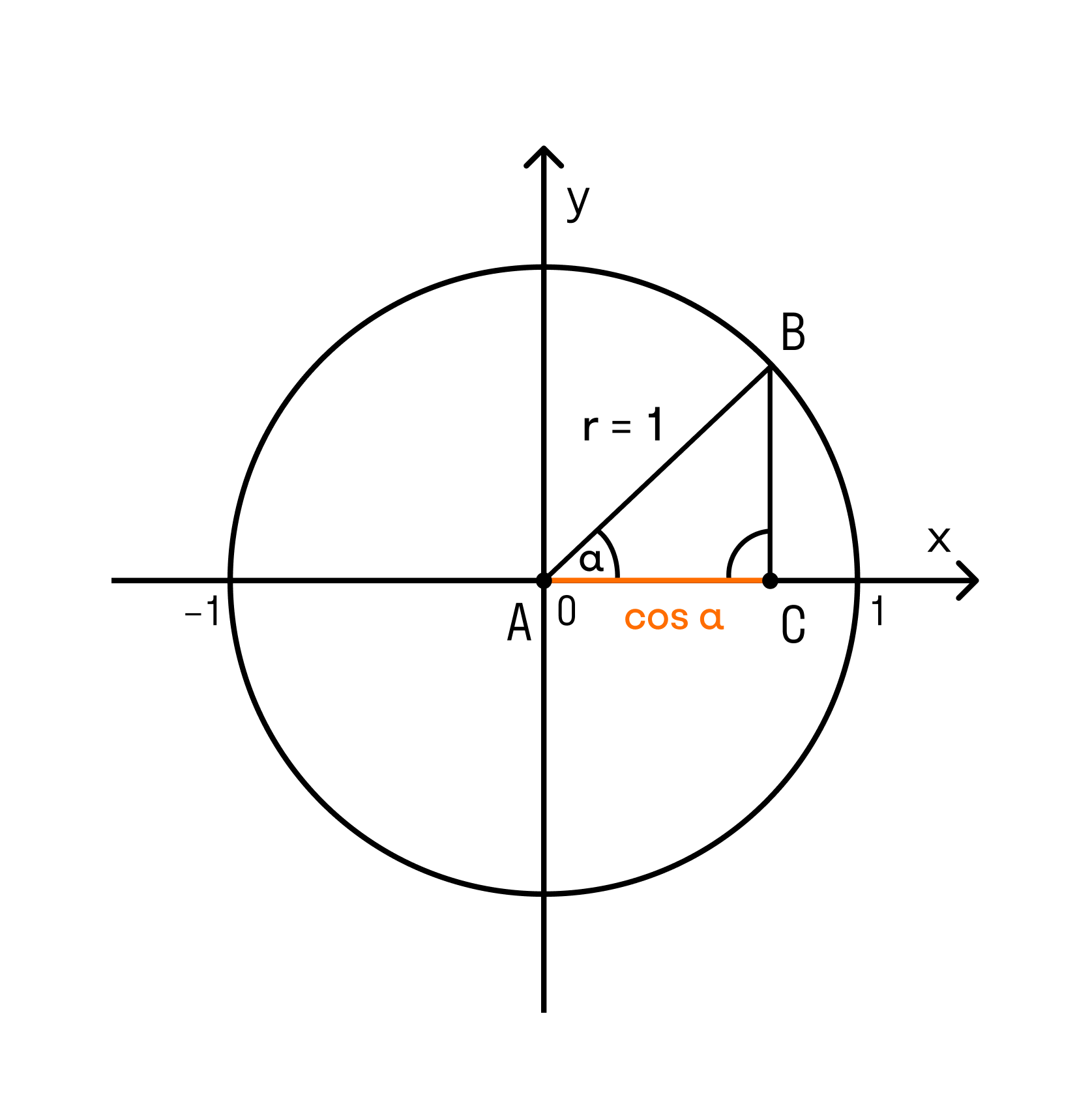
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!