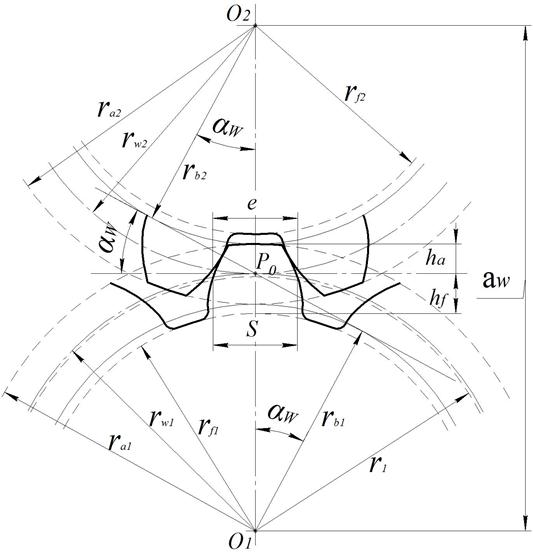
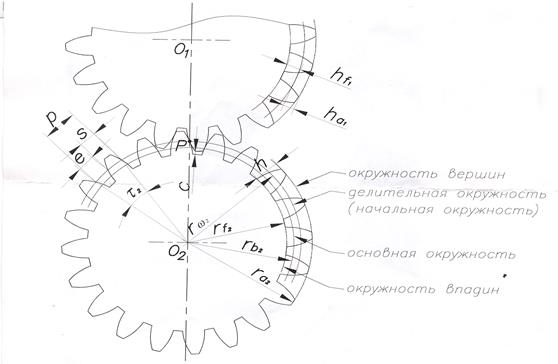
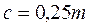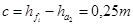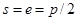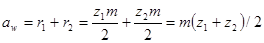какая окружность называется основной

Какая окружность называется основной

Для параметров зубчатого колеса справедливы следующие соотношения

– диаметр окружности произвольного радиуса,

– диаметр делительной окружности,

– шаг по окружности произвольного радиуса,

– шаг по делительной окружности,

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.

Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:

Из вариантов изготовления по способу копирования можно отметить:

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать

Виды зубчатых колес (Классификация по величине смещения) .

В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.

Подрезание и заострение зубчатого колеса .

На рис. 12.7 изображены два эвольвентных зуба для которых

Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого

При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

Источник

Основные параметры, характеризующие зубчатые колеса

Понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандарты устанавливают термины, определения и обозначения, а также методы расчета геометрических параметров.

Меньшее из пары зубчатых колес называют шестерней,а большееколесом.Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2. (РИС 5.8).

В зубчатых колесах различают следующие поверхности или окружности: начальная, основная, вершин зубьев, впадин зубьев, делительная.

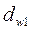
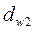
Начальными ( и ) называются такие окружности (поверхности), которые катятся друг по другу без скольжения, то есть являются центроидами в относительном движении колес. Параметры, относящиеся к начальным окружностям, обозначаются индексом w.

Делительная окружность (поверхность) – это окружность, для которой модуль является стандартным. В некоррегированных, нарезанных несмещенной зубчатой рейкой зубчатых колесах начальная и делительная окружности совпадают. Параметрам, относящимся к делительной окружности или поверхности, дополнительного индекса не приписывают.

Кроме того, различают индексы, относящиеся:

b- к основной поверхности или окружности;

а – к поверхности или окружности вершин (головок) зубьев;

f – ­к поверхности или окружности впадин (ножек) зубьев.

Зацепление зубчатых колес характеризуется:

и – числами зубьев шестерни и колеса;

– межосевым расстоянием (расстоянием между центрами начальных окружностей);

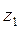
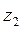
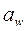
р – шагом зубьев по делительной окружности (часть делительной окружности, заключенной между одноименными точками двух соседних зубьев);

s– толщина зуба по делительной окружности (дуга делительной окружности вмещающая один зуб);

е – ширина впадины (дуга делительной окружности между двумя соседними зубьями);

– высота ножки зуба (часть профиля зуба внутри делительной окружности);

– высота головки зуба (часть профиля зуба, выступающая за делительную окружность);

– угол зацепления или профильный угол рейки;

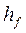
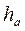
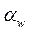
Как видно из Рис 5.8, шаг зацепления равен

.

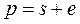
При передаче непрерывного движения сопряженными колесами шаг зацепления должен быть одинаков для обоих колес. Тогда соотношение между числами зубьев и диаметрами делительных окружностей колес будет:

и .

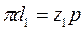
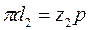
Тогда 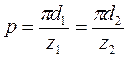(5.8)

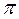
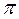
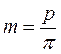
При определении шага в формулу (5.8) входит трансцендентное число . Это затрудняет подбор размеров зубчатых колес при проектировании. Поэтому для определения размеров колес в качестве основного параметра, определяющего эти размеры, принят модуль зацепления, определяемый как отношение шага зацепления по делительной окружности к числу и округленный до стандартного значения.

. (5.9)

Тогда диаметры делительных окружностей, выраженные через модуль, определяться как:

и (5.10)

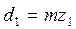
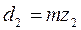
Высота головки зуба

(5.11)

(5.12)

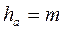
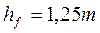
и, как видно из (5.12), будет больше высоты головки на величину осевого смещения, которое для стандартных колес определяется как

Диаметр окружности вершин зубьев

(5.13)

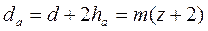
Диаметр окружности впадин

(5.14)

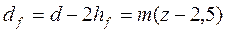
По делительной окружности толщина зуба равна ширине впадины тогда

(5.15)

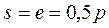
Межосевое расстояние будет

(5.16)

Источник

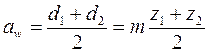
Зубчатого колеса

Окружность вершин – окружность, описанная из центра колеса и ограничивающая вершины зубьев.

Окружность впадин – окружность, описанная из центра колеса и ограничивающая его впадины со стороны колеса.

Делительная окружность– окружность, на которой расстояние между одноименными сторонами двух соседних зубьев равно шагу зуборезного инструмента. Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

Модуль – значение следует выбирать по СТ СЭВ-310-76. Этим стандартом дан ряд значений от 0,05 до 100 мм:

– 1 ряд (предпочтительный): 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25 и т. д.;- 2 ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; И; 14; 18; 22 и т. д.

Окружной шаг зубчатого зацепления р – есть расстояние между одноименными точками двух соседних зубьев колеса, измеренное по дуге делительной окружности.

Высотой зуба h – называется радиальное расстояние между окружностью вершин и окружность впадин.

Разница в высоте ножки зуба одного колеса и высоте головки зуба другого необходима для образования радиального зазора:

Теоретически толщина зуба s и ширина впадины e по делительной окружности равны между собой:

Однако, чтобы создать боковой зазор, необходимый для нормальной работы зубчатой пары, зуб делается несколько тоньше, вследствие чего он входит во впадину свободно.

Межосевое расстояние двух сцепляющихся зубчатых колес определяется по формуле:

Передаточное отношение (основной закон зацепления):

(5.1)

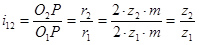
№ п/п	Название	Формула для вычисления (без смещения режущего инструмента)
Диаметр окружности вершин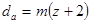
Диаметр окружности впадин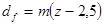
Диаметр основной окружности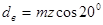
Диаметр начальной окружности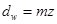
Диаметр делительной окружности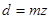
Модуль	m
Число зубьев	z
Шаг по делительной окружности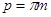
Высота зуба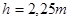
Высота головки зуба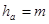
Высота ножки зуба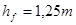
Толщина зуба по делительной окружности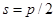
Ширина впадины между зубьями по делительной окружности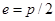
Угловой шаг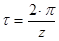

Методы изготовления эвольвентных зубчатых колёс

В основу изготовления эвольвентных зубчатых колёс положено два принципиально отличительных метода.

Способ копирования

Рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности (подобны ей, то есть заполняют эту поверхность как отливка заполняет форму).

Нарезание зубчатых колес осуществляется профилированной пальцевой 1 или дисковой 2 фрезами (рис.5.3 а, б), проекция режущих кромок которых соответствует конфигурации впадин. Резание производится в следующем порядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются до тех пор, пока не будут прорезаны все впадины.

Достоинства:

1.Возиожность нарезания зубьев 6на универсальном фрезерном оборудовании.

Недостатки:

1.Огромная номенклатура режущего инструмента (равна сочетанию модуля и числа зубьев);

2.Принципиальная неточность нарезания зубьев;

3.Нетехнологичность инструмента, малая производительность.

Способ огибания (обкатки)

Достоинства:

1.Принципиальная точность нарезания зубьев;

2.Резкое сокращение номенклатуры и технологичность инструмента;

Недостатки:

1.Требуется специальное зубонарезное оборудование.

Источник

Всё про окружность и круг

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Источник

ТММ 30вопросов

1. Нарезание колес с эвольвентным профилем зуба в приборостроении производится методом обкатки (при индивидуальном производстве колеса нарезаются методом деления). Сущность метода обкатки заключается в том, что в процессе нарезания зубьев заготовке (нарезаемому колесу) и инструменту сообщают то относительное движение, которое имели бы два зубчатых колеса (или колесо и рейка), находящиеся в правильном зацеплении.

3. Нулевое колесо (рисунок 4.5 а). Делительная прямая рейки перекатывается по делительной окружности колеса. У такого колеса толщина зуба и ширина впадины между зубьями по делительной окружности равны между собой. (колеса, у которых делительная окружность совпадает с начальной.) (Какие зубчатые колеса называются нулевыми? Колеса, у которых делительная окружность совпадает с начальной)

4. Что называется модулем зубчатого колеса, в чем он измеряется? Параметр, принятый в качестве основной единицы для определения основных параметров зубчатых колес. Модуль –это величина, которая определяется как частное от деления шага по делительной окружности на =3,14. Модуль измеряется в мм.

6. Корригированные (исправленные) колеса (рисунки 4.5 б и в) нарезанные

смещённой инструментальной рейкой. В этих случаях делительная окружность

колеса не соприкасается с делительной прямой рейки. Корригирование зубчатых

колёс производится с целью улучшения качества (исправления) зацепления, устранения

подреза ножки зуба, увеличения коэффициента перекрытия, уменьшения износа, повышения

7. Δ = 0 s = e = p/2 нулевое зубчатое колесо; Δ > 0 s > e положительное зубчатое колесо;

Источник