какая операция называется конъюнкцией
Значение слова «конъюнкция»
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).
конъю́нкция
1. матем. лог. логическое высказывание, получаемое путём объединения двух простых утверждений союзом «и»
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: седлать — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «конъюнкция»
Предложения со словом «конъюнкция»
Понятия со словом «конъюнкция»
Отправить комментарий
Дополнительно
Предложения со словом «конъюнкция»
Под p понимается любое высказывание, под \ p – отрицание высказывания, знак \ перед формулой – отрицание двух высказываний, ал – знак конъюнкции.
Строгая дизъюнкция эксплицируется просто как отрицание конъюнкции.
Сложное высказывание, полученное с помощью двух (или более) высказываний при помощи слова «и», называется конъюнкцией.
Синонимы к слову «конъюнкция»
Морфология
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Какая операция называется конъюнкцией
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Конъюнкция
Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты:
в инфиксной записи:
,
по аналогии с умножением в алгебре знак логического умножения может быть пропущен: 
,
в префиксной записи:
.
. Результат также принадлежит множеству 
может использоваться любая другая пара подходящих символов, например 
или 
или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, 
false» border=»0″ />, при цифровом обозначении старшинство естественно 
0″ border=»0″ />.  |  |  |
 | | |
|  | |
| | |
| | |
для тернарной конъюнкции
| X | Y | Z | X  Y Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Многозначная логика
Операция, называемая в двоичной логике конъюнкция, в многозначных логиках называется минимум: , где 
, а 
— значность логики. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 
и 
.
Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» имеют смысл только в двоичной логике, а при переходе к многозначным логикам теряют смысл.
Классическая логика
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции: 
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
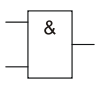
Схемотехника
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Программирование
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата 
или 
. Например:
Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:
Проверка истинности выражения в данном случае остановится после проверки переменной a, т.к. дальнейшее сравнение не имеет смысла.
Результат будет равен , если оба операнда равны (для числовых типов не равны ). В любом другом случае результат будет равен .
При этом применяется стандартное соглашение: если значение левого операнда равно , то значение правого операнда не вычисляется (вместо может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = |  |
| b = |  |
| то | |
| a И b = |  |
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как , а «ложь» как . При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».
Примечания
См. также
КОНЪЮНКЦИЯ — (от лат. conjunctio союз, связь), в широком смысле сложное высказывание, образованное с помощью союза «и». В принципе можно говорить о К. бесконечного числа высказываний (напр., о К. всех истинных предложений математики). В логике К. наз … Философская энциклопедия
конъюнкция — логическое произведение; операция. Ant. дизъюнкция Словарь русских синонимов. конъюнкция сущ., кол во синонимов: 1 • операция (457) Словарь синонимов ASIS. В.Н … Словарь синонимов
Конъюнкция — Конъюнкция ♦ Conjonction Соединение или связь. В логике конъюнкцией называют высказывание, состоящее из двух или более высказываний, связанных соединительным союзом «и»: «p и q» – пример конъюнкции. Конъюнкция истинна только при том условии … Философский словарь Спонвиля
КОНЪЮНКЦИЯ — (от лат. conjunctio союз связь), логический эквивалент союза и ; операция, формализующая логические свойства этого союза … Большой Энциклопедический словарь
конъюнкция — логическое умножение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы логическое умножение EN conjunction … Справочник технического переводчика
КОНЪЮНКЦИЯ — логическая операция, образующая сложное высказывание из двух высказываний, объединённых с помощью логического союза «И». Логический переключательный элемент, реализующий функцию К., называется схемой совпадения или вентилем. С помощью этой… … Большая политехническая энциклопедия
КОНЪЮНКЦИЯ — (Coniunctio лат.) в буквальном смысле термин «конъюнкция» используется в алхимии для обозначения химических комбинаций, рождения нового элемента, психологически он указывает на союз противоположностей и на появление новых возможностей. Юнг… … Словарь по аналитической психологии
Какая операция называется конъюнкцией
§ 2. Логические операции. Формализация высказываний
Сейчас мы познакомимся с шестью основными логическими операциями. Каждая из них имеет несколько названий и обозначений.
Названия операции
Возможные обозначения
Конъюнкция, логическое умножение, операция И, операция AND.
`&, ^^, *,` по аналогии с алгебраическим умножением может никак не обозначаться
Дизъюнкция, нестрогая дизъюнкция, логическое сложение, операция ИЛИ, операция OR.
Строгая дизъюнкция, разделительная дизъюнкция, исключающее ИЛИ, сложение по модулю `2`.
Эквивалентность, эквиваленция, равенство, равнозначность.
Импликация, следование, следствие
Теперь для того чтобы строго определить эти логические операции, нам нужно для каждой из них выписать таблицу истинности. Все перечисленные операции кроме отрицания имеют два операнда. Знак операции в выражениях пишется между операндами (как в алгебре чисел). Операция отрицания имеет один операнд и в выражениях записывается либо в виде черты над операндом, либо в виде символа «приставка» слева от операнда.
1) `p` и `q` ложны. Это значит, что четырёхугольник не является квадратом и его стороны не равны. Это возможная ситуация.
2) `p` – ложно, `q` – истинно. Это значит, что четырёхугольник не является квадратом, но стороны у него равны. Это возможно (ромб).
3) `p` – истинно, `q` – истинно. Это значит, что четырёхугольник является квадратом и стороны у него равны. Это возможная ситуация.
4) `p` – истинно, `q` – ложно. Это значит, что четырёхугольник является квадратом, но стороны у него не равны. Это невозможная ситуация.
Очень часто вместо «присвоим логическим переменным эти высказывания» говорят «обозначим высказывания следующим образом». В дальнейшем мы тоже будем использовать этот речевой оборот.
Логические операции. ➞ Что такое конъюнкция, дизъюнкция, импликация
Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.
Основные положения
Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.
Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).
Примером таким высказываний будут являться:
Логические высказывания делятся на два типа — простые и сложные.
В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.
Булево выражение – это символическое (знаковое) описание высказывания.
Операции
Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.
Конъюнкция
Конъюнкция (булево умножение) — функция, по своему смыслу приближенная к союзу «И». При выполнении конъюнкции результат истинен (равен 1) тогда и только тогда, когда истинны ВСЕ переменные. Если хотя бы одно из высказываний ложно, то ложно и всё выражение (равно 0).
Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:
Дизъюнкция
Дизъюнкцией называется функция булева сложения. По смыслу дизъюнкция приближена к союзу «ИЛИ». В результате выполнения данной функции результирующие выражение является истинным, когда хотя бы одно из высказываний в этом выражении тоже истинно.
Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.
Инверсия
Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.
Импликация
Также называется булевым следованием. В русском языке данной функции соответствует оборот «Если …, то …». Например, если на улице гремит, то стоит пасмурная погода.
Эквивалентность
Булева тождественность или равенство. На простом языке будет обозначено как «… эквивалентно (равно) …». Результат будет истинным тогда, когда все значения в выражении будут иметь одинаковую истинность.
Обозначается с помощью трех черточек или ⟺.
Порядок выполнения операций
Логические операции выполняются в следующем порядке:
Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.
Пример
Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:
Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:
Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.
Таблица истинности для всех отрезков:
Ответ: A = [3,11].
Заключение
Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.
- какая скульптура микеланджело удостоилась личной похвалы леонардо да винчи 5 букв
- код на симс на потребности повышение максимум