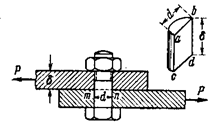
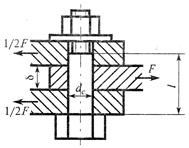
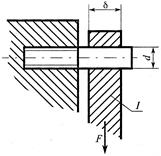
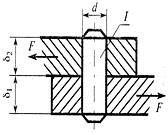
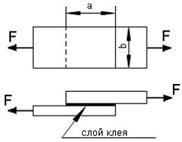
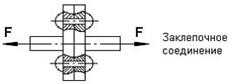
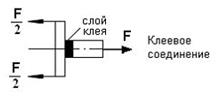
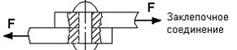
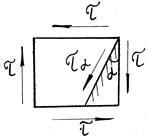
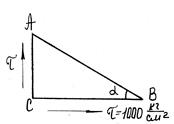
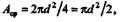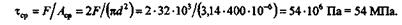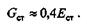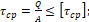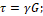какая площадь принимается за расчетную при сдвиге

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наи­большее напряжение возникающее в ней (рабочее напряжение) не должно превышать допускаемое.

Расчетная формула при сдвиге

читается следующим образом: касательное напряжение при сдвиге, вы­численное по формуле 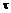= Q/A, не должно превышать допускаемое.

По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называет­ся срезом (применительно к металлическим деталям) или скалыва­нием (применительно к неметаллическим конструкциям).

Допускаемое напряжение на срез выбирают для пластичных мате­риалов в зависимости от предела текучести. В машиностроении для штифтов, болтов, шпонок и т. п. принимают

Для древесины допускаемые напряжения на скалывание во врубках колеблются в пределах от 0,5 до 1,4 МПа и зависят от сорта дерева и на­правления врубки по отношению к направлению волокон.

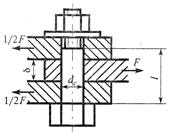
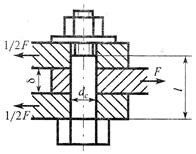
При расчетах на срез в случае, если соединение осуществляется не­сколькими одинаковыми деталями (болтами, заклепками и т. д.), полага­ют, что все они нагружены одинаково.

Расчеты соединений на срез обычно сопровождают проверкой проч­ности этих соединений на смятие.

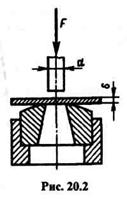
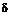
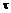
Пример 20.1. Определить силу F, необходимую для пробивания квадратно­го отверстия размером а = 25 мм в стальной полосе толщиной = 10 мм, если предел прочности при срезе _в= 360 МПа. Определить напряжения сжатия в пу­ансоне (рис. 20.2).

Решение. Определим разрушающую нагрузку F:

Площадь среза A_ср равна площади боковой поверхности пробитого отверстия

_с=F/A,

где А — площадь поперечного сечения пуансона;

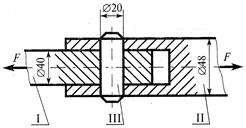
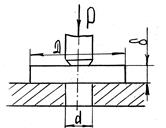
Пример 20.2. Определить напряжения смятия и среза в головке стержня, растягиваемого силой F= 100 кН. Дано: D= 32 мм, d= 20 мм, h = 12 мм (рис. 20.3).

Решение. Определим площадь смятия А_сми площадь среза А_ср головки. Пло­щадь опорной поверхности головки, работающей на смятие, равна

Площадь среза равна площади боковой поверхности цилиндра диаметром d и высотой h:

Определим напряжения смятия и среза головки:

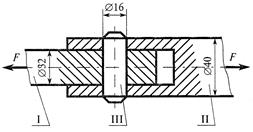
Пример 20.3. В условиях примера 19.6 определить напряжения среза в бол­те (см. рис. 19.13,б).

Решение. Напряжения среза в болте вычисляем по формуле = F/A_ср.

Площадь среза A_ср представляет собой две площади поперечного сечения болта:

Деформация и закон Гука при сдвиге

Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abсd,на грани которого действуют только касательные напряжения 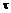, а противополож­ную грань параллелепипеда представим жестко защемленной (рис. 20.4). Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bс по отношению к сечению, принятому за неподвижное. Деформа­ция сдвига характеризуется углом и называется углом сдвига или относительным сдвигом (так как этот параметр не зависит от

расстояния h,на котором происходит сдвиг). Величина bb₁, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом. Относительный сдвиг 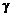выражается в радианах.

Напряжения и деформации при сдвиге связаны меж­ду собой зависимостью, которая называется законом Гука при сдвиге.

Закон Гука при сдвиге справедлив лишь в определен­ных пределах нагружения и формулируется так: каса­тельное напряжение прямо пропорционально относи­тельному сдвигу.

Математически закон Гука можно записать в виде равенства

Коэффициент пропорциональности G характеризует жесткость мате­риала (т. е. способность сопротивляться упругим деформациям) при сдви­ге и называется м о д у л е м сдвига или модулем упругости второго рода.

Модуль упругости и напряжение выражаются в одинаковых единицах:

Значения G, МПа, для некоторых материалов:

Чугун. 4,5 10 4

Сталь. 8,1 10 4

Медь. ………………. (4,0. 4,9) 10 4

Латунь. (3,5. 3,7) 10 4

Дерево. 0,055 10 4

В заключение отметим, что между тремя упругими постоянными Е, G и v существует следующая зависимость:

Принимая для сталей v 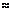0,25, получаем

Дата добавления: 2018-04-15 ; просмотров: 1745 ; Мы поможем в написании вашей работы!

Источник

Какая площадь принимается за расчетную при сдвиге

Тестовые вопросы по теме «Смятие и сдвиг»

– Какие виды деформаций испытывает данное соединение?

1. Растяжение и изгиб;

3. Изгиб и кручение;

4. Растяжение и сдвиг.

– Какая площадь принимается за расчетную при смятии?

1. площадь поверхности заклепки;

3. площадь поперечного сечения.

– Как направлены к плоскости поперечного сечения напряжения при сдвиге?

1. совпадают с плоскостью сдвига;

2. перпендикулярно к плоскости сдвига;

– Чему равны главные напряжения при сдвиге?

1. σ 1,3 =0° ;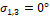

2. σ 1,3 =±2 τ ;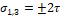

3. σ 1,3 =± τ .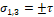

– Какие виды деформаций испытывает головка болта?

1. изгиб с кручением;

– Во сколько раз изменится допускаемая нагрузка на сварное соединение, если толщина шва уменьшится вдвое (при прочих равных условиях)?

1. уменьшится в четыре раза;

2. уменьшится вдвое.

– Закон Гука при сдвиге:

1. τ = G ∙ γ ;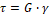

2. τ = Q A ≤ τ ;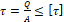

3. τ = T KP ∙ ρ J p ;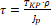

4. τ = Gρθ .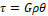

– Коэффициент пропорциональности G называется:

2. модулем упругости второго рода;

3. модулем продольной упругости;

4. верны ответы 1 и 2.

– Модуль сдвига имеет размерность:

3. верны ответы 2 и 4;

1. относительным сдвигом;

2. углом закручивания;

3. абсолютной деформацией;

4. нет правильного ответа.

– Чистым сдвигом называется такой случай плоского напряженного состояния:

1. при котором в окрестности данной точки может быть выделен элементарный параллелепипед с боковыми гранями, находящимися под действием одних лишь касательных напряжений;

2. при котором в окрестности данной точки может быть выделен элементарный параллелепипед с боковыми гранями, находящимися под действием одних лишь нормальных напряжений;

3. верны ответы 1 и 2.

– Условие прочности на смятие имеет вид:

1. σ c м = Q A ;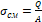

2. τ cp = Q A ≤ τ cp ;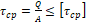

3. σ c м = Q A ≤ σ c м ;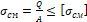

4. σ = E ∙ ε .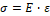

– Какое из приведенных выражений будет соответствовать проектировочному расчету на смятие?

1. A ≥ Q τ cp ;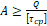

2. A ≥ Q σ c м ;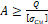

3. σ c м = Q A ≤ σ c м ;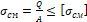

4. τ = T ∙ ρ J p .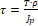

– Какое из приведенных выражений будет соответствовать проверочному расчету на смятие?

1. σ c м = Q A ≤ σ c м ;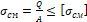

2. τ cp = Q A ≤ τ cp ;

3. τ max = T max W p ≤ τ ;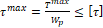

4. A ≥ Q σ c м .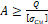

– Формула для определения максимальной допускаемой нагрузки при расчете на смятие:

1. M X max = W X ∙ σ ;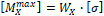

2. Q max ≤ A σ см ;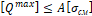

3. Q max ≤ A τ ср ;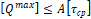

4. N max = A σ .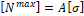

– Выбрать формулу для расчета напряжения сдвига в поперечном сечении болта

1. σ = N A ;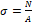

2. τ = N A ;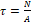

3. τ = M z W p ;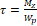

4. σ = Q A .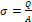

– Рассчитать площадь смятия внутреннего листа соединения, нагруженного растягивающей силой

– Проверить прочность на смятие внутреннего листа соединения, если допускаемое напряжение смятия материала листа 120 МПа. Листы соединены болтом, поставленным без зазора. Соединение нагружено растягивающей силой F = 50,4 кН; d_c = 21 мм; l =45 мм; δ = 20 мм

4. Для ответа данных недостаточно.

– Выбрать формулу для расчета напряжения в поперечном сечении детали при сдвиге

1. σ = N A ;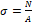

2. τ = Q A ;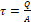

3. τ = M z W p ;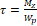

4. σ = M x W x .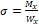

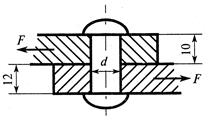
– Рассчитать величину площади смятия штифта, изображенного на рисунке

– Из расчета на смятие определить количество заклепок, необходимое для передачи внешней силы. F =120кН, [ τ_ср ] = 80 МПа, [ σ_см ] = 240 МПа, d = 20 мм.

– Выбрать формулу для расчета напряжения в поперечном сечении детали при сдвиге

1. τ = Gγ ;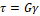

2. τ = Q A ;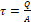

3. σ = N A ;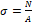

4. τ = M z W p .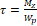

– Рассчитать величину площади смятия штифта, изображенного на рисунке

– Из расчета на смятие определить количество заклепок, необходимое для передачи внешней силы. F =180кН, [ τ_ср ] = 80 МПа, [ σ_см ] = 240 МПа, d = 16 мм.

– Из условия прочности листа на смятие определить допускаемую нагрузку, если [ τ _ср ] = 100 МПа; [ σ_см ] = 240 МПа

– Условие прочности при сдвиге

1. Q ≤ τ ∙ A ;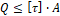

2. τ max = Q A ≤ τ ;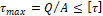

3. τ max τ ≤1 .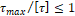

1. τ = F ab ≤ τ _;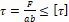

2. τ = 2 F ab ≤ τ _;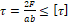

3. τ = F ab ≥ τ _;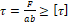

4. τ = F 2 ab ≤ τ _.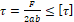

– На срез (на сдвиг) рассчитывается соединение, показанное на рисунке.

1.

2.

3.

– Какую механическую характеристику материала листа надо знать, чтобы определить силу, необходимую для продавливания отверстий?

1. предел текучести;

2. предел прочности на растяжение;

3. предел прочности на срез.

– Во сколько раз изменится допускаемая нагрузка на сварное соединение, если толщина шва уменьшится вдвое (при прочих равных условиях)?

1. уменьшится в четыре раза;

2. уменьшится вдвое.

– Чему равна сумма нормальных напряжений на любых 3-х взаимно перпендикулярных площадках?

– На основе какого из допущений, принятых в курсе сопротивления материалов, составлены выражения обобщенного закона Гука?

1. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке.

2. Материал конструкции обладает свойством идеальной упругости.

3. Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.

4. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.

– Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?

– Чему равно относительное изменение объема при сдвиге?

1. ∆ V V = ε 1-2 μ ;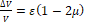

2. ∆ V V = με ;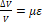

– Какая теоретическая зависимость существует между допускаемым напряжением на растяжение и допускаемым напряжением на сдвиг (по четвертой теории прочности)?

1. τ =0,4 σ ;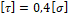

2. τ =0,5 σ ;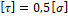

3. τ =0,6 σ .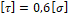

– Укажите в круге Мора отрезки, соответствующие главным напряжением.

– Какие деформации в материале возникают при чистом сдвиге?

1. угловая и продольная деформации;

2. продольная деформация;

3. угловая деформация.

1. τ α = τcos 2 α ;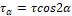

2. τ α = τsin 2 α ;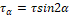

– Укажите формулу, выражающую закон Гука при сдвиге

1. σ = εE ;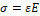

2. τ = γG ;

3. τ = G γ .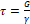

– Какая зависимость существует между модулем сдвига и модулем упругости?

1. G = E 2 1- μ ;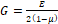

2. G = E 2 1+ μ ;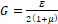

– Какие виды деформаций испытывает шпоночное соединение?

2. сдвиг и кручение;

3. срез и растяжение.

– Как записывается условие прочности при смятии?

1. 4 Q 8 πd ≤ σ см ;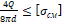

2. Q A см ≤ σ см ;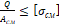

3. 4 Q π d 2 ≤ σ см .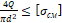

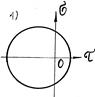
– Укажите напряженное состояние элемента, соответствующего изображенному кругу Мора

1. 2. 3.

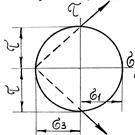
– Как распределяются касательные напряжения в поперечном сечении при сдвиге?

1. по закону прямой ;

3. по закону параболы.

– Под каким углом к плоскости сдвига наклонены главные площадки?

– Укажите круг Мора для чистого сдвига?

1. 2. 3.

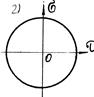
– Чему равна потенциальная энергия объема при чистом сдвиге?

1. σ 2 2 E ;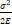

2. τ 2 2 G ;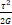

– Какие напряжения (нормальные или касательные) возникают при смятии?

1. нормальные и касательные;

– Какая теоретическая зависимость существует между допускаемым напряжением на растяжение и допускаемым напряжением на сдвиг (по третьей теории прочности)?

1. τ =0,6 σ ;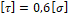

2. τ =0,5 σ ;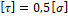

3. τ =0,8 σ .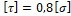

– Чему равно допускаемое напряжение при сдвиге для пластичных материалов?

1. τ =0,7÷0,8 σ ;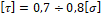

2. τ =0,6÷0,7 σ ;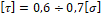

3. τ =0,5÷0,6 σ .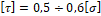

– Как записывается условие прочности при сдвиге?

1. Q A сд ≥ τ сд ;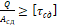

2. 4 Q π d 2 ≥ τ сд ;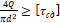

3. 4 Q A сд ≥ τ сд .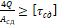

– Во сколько раз увеличится несущая способность соединения при расчете на смятие, если диаметр заклепок увеличится на 50%?

– По какой формуле определяется работа, затрачиваемая на сдвиг?

1. A = 1 2 EF F N x 2 dx ;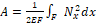

2. A = 1 2 GF F Q x 2 dx ;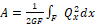

3. A = 1 EI F M x 2 dx .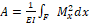

– На какие виды деформаций рассчитывают шлицевое соединение?

3. кручение и растяжение.

– Укажите формулу для расчета шайбы на смятие

2. 4 P πDδ ≤ σ см ;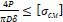

3. 4 P π d δ ≤ σ см .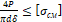

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник