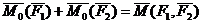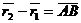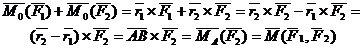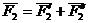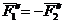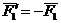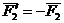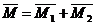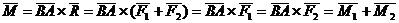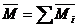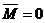какая плоскость называется плоскостью действия пары
Пары сил



Действие пары сил на твердое тело сводится к вращательному эффекту, мерой которой является векторная величина m(или M), называется моментом пары сил.
Характеристики вектора пары сил
1) Модуль этого вектора равен произведению модуля силы пары на ее плечо:
2) Вектор m расположен на прямой, перпендикулярной плоскости действия пары;
Вектор m направлен вдоль указанной прямой так, чтобы из его острия вращениея, которое стремиться сообщить телу пара сил, было видно происходящим против хода часовой стрелки.
Вектор-момент пары m является вектором свободным.
1) пару сил можно переносить куда угодно в плоскости действия пары;
2) пару сил можно переносить из данной плоскости в любую плоскость параллельную данной;
3) у данной пары можно произвольно менять модули сил и длинну плеча, сохраняя неизменным ее момент.
— Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу (теорема об эквивалентности пар).
— Система пар, действующая на абсолютно твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов сложенных пар.
(теорема о сложении пар)
Теорема о параллельном переносе силы.
— Силу, не изменяя оказываемого ею действия на твердое тело, можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил с моментом, равным моменту заданной силы относительно ее новой точки приложения.
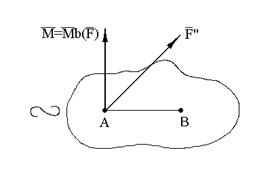
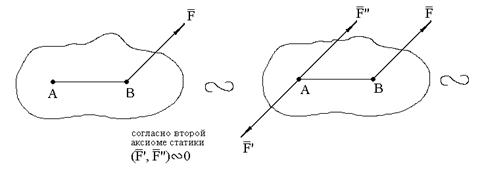
систему силы Fa силой Fb’ и парой сил (F’, F’’) называют привидением силы F к заданному центру ( в данном случае к центру B).
Теорема о привидении системы сил к одному центру.
— Действие любой произвольной системы сил на твердое тело эквивалентно действию в произвольной точке О этого тела силы R, равной главному вектору системы сил,
и пары сил, момент которой Mo равен главному вектору системы сил, и пары сил, момент которой Mo равен главному моменту системы сил относительно центра О.
Величина R, равная геометрической сумме всех сил, называется главным вектором системы сил;

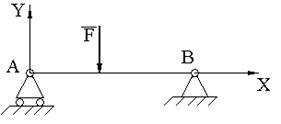
Равновесие тела под действием системы сил.
Для равновесия произвольной пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы ее главный вектор и главный момент относительно любого центра (точки) О был равны нулю:
Эти равенства являются векторными условиями для любой системы сил.
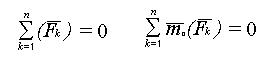 |
Проектируя эти векторные равенства на координатные оси, получили шестьаналитических условий:
∑Fkx = 0; ∑Fky = 0; ∑Fkz = 0;
∑Mx(Fk) = 0 ; ∑My(Fk) = 0; ∑Mz(Fk) = 0;
Основная форма условия равновесия при действии на тело поской системы сил.
∑Fkx = 0; ∑Fky = 0; ∑Mо(Fk) = 0.
Вторая форма условий равновесия:
∑Ma(Fk) = 0 ; ∑Mb(Fk) = 0; ∑Fkx = 0.
Третья форма условий равновесия:
∑Ma(Fk) = 0 ; ∑Mb(Fk) = 0; ∑Mz(Fk) = 0;

Пара сил и ее свойства



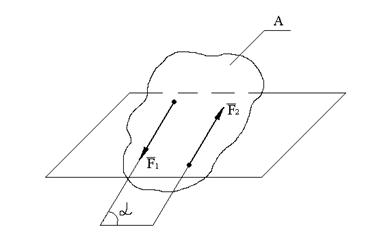
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело (рис. 17).
Плоскость 
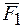
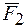
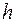
Вращающее действие пары на твердое тело зависит от модуля сил пары 
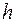
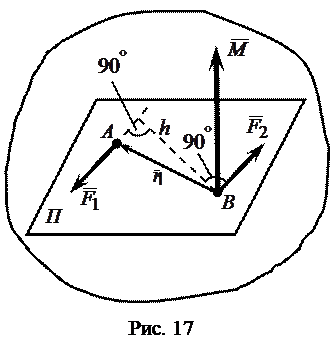
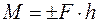
Момент пары, как и момент силы, измеряется в 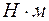
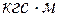
Алгебраическая сумма моментов сил пары относительно произвольной точки в плоскости ее действия не зависит от выбора этой точки и равна моменту пары. Действительно, определим сумму моментов сил 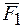
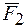
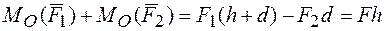
где 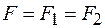
Так как 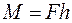
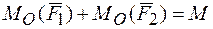
Если силы и пары, приложенные к телу, лежат в разных плоскостях, то момент пары, как и момент силы, необходимо рассматривать как вектор. Вводим в связи с этим общее определение 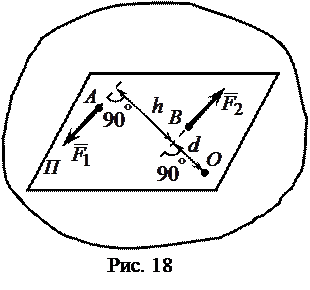
Моментом пары является вектор 
Модуль вектора 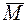
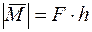
Из определения векторов 
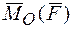
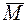
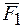
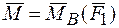
Используя формулу 16, имеем:
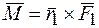
Таким образом, момент пары можно представить в виде векторного произведения (23), в котором 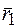
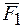
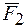
Свойства пар выражаются следующими теоремами, которые приводятся здесь без доказательств.
1) Действие пары на твердое тело не изменится, если перенести пару в плоскости ее действия в любое другое положение.
2) Действие пары на твердое тело не изменится, если модуль сил пары и ее плечо изменить так, чтобы модуль момента пары сохранился неизменным.
3) Действие пары на твердое тело не изменится, если перенести пару в любую другую плоскость, параллельную плоскости ее действия.
4) Система пар, приложенных к твердому телу, может быть заменена одной результирующей парой с моментом 
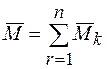
Из теорем следует, что пару, выраженную вектором 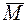
Вопросы для самопроверки к разделу 2
1. Определить момент силы относительно точки как алгебраическую величину, как вектор.
2. В каком случае момент силы относительно точки равен нулю?
3. Что называется моментом силы относительно оси?
4. В каких случаях момент силы относительно оси равен нулю?
5. Можно ли открыть дверь, если все приложенные к ней силы располагаются в плоскости двери?
6. Какова зависимость между моментами силы относительно оси и относительно точки, лежащей на этой оси?
7. Выведите формулы для моментов силы относительно трех координатных осей, используя представление о векторе момента силы относительно точки в виде векторного произведения.
8. Что называется парой сил? Чему равен момент пары?
9. Какие факторы определяют действие пары на твердое тело?
10. Как направлен, где приложен вектор момента пары?
11. Сформулируйте условие равновесия системы пар сил, приложенных к твердому телу.
12. Могут ли уравновесить друг друга две пары сил, лежащие в параллельных плоскостях; в пересекающихся плоскостях?
13. Каким образом можно изменять плечо и модуль сил пары, не изменяя действие пары на твердое тело?
14. Как складываются пары, лежащие в одной плоскости; в пересекающихся плоскостях?
Условия равновесия пар сил.
Лекция 4
Краткое содержание: Пара сил. Теорема о сумме моментов пары сил. Теорема об эквивалентности пар сил. Теорема о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил. Условия равновесия пар сил.
ПАРА СИЛ
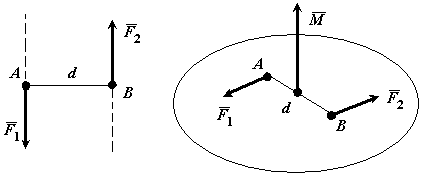
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.
Плоскостью действия пары сил называется плоскость в которой расположены эти силы.
Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.
Моментом пары сил называется вектор 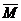
 |
Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.
Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).
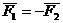
Что и требовалось доказать.
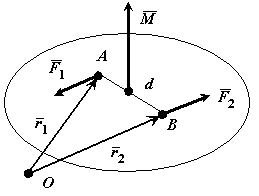 |
Рис. 4.2
Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.
Доказательство: Пусть на твердое тело действует пара сил 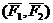
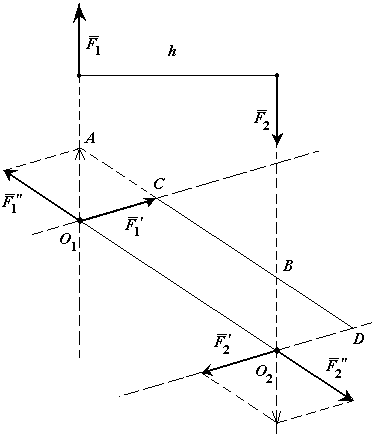
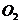
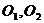
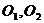
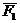
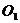
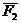
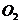
Так как 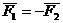
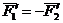
Поэтому 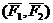
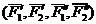
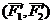
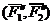
Таким образом мы заданную пару сил 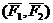
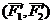
Момент исходной пары сил 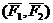
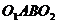
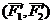
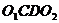

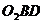
Что и требовалось доказать.
1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.
2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.
Теорема о переносе пары сил в параллельную плоскость.Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.
Доказательство: Пусть на твердое тело действует пара сил 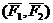
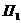
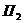
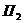
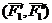
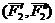
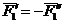
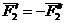
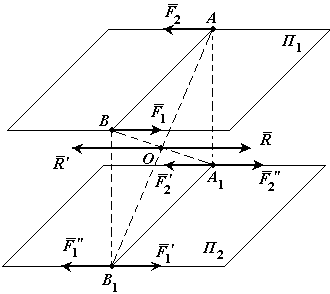


Сложим две равные и параллельные силы 
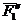
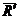
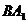
Так как 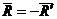
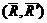
Таким образом пара сил 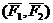
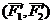
Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.
Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.
Теорема о сложении пар сил.Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.
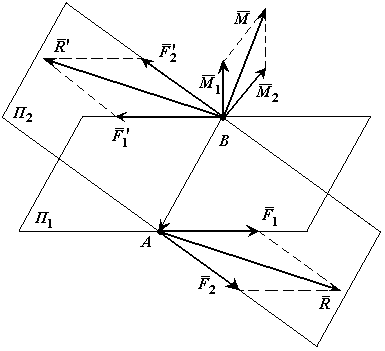 |
Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил 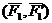
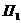
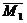
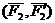
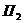
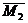
Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, 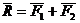
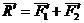
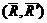
Что и требовалось доказать.
Условия равновесия пар сил.
Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.
Теорема.Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.
Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.