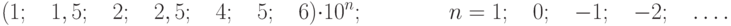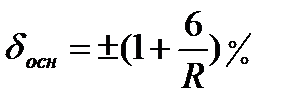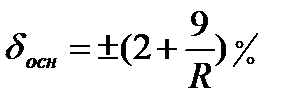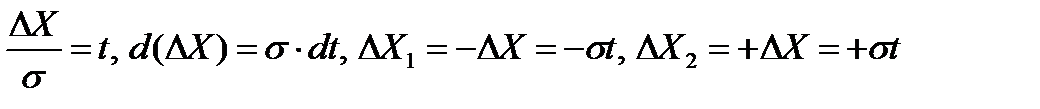какая погрешность называется аддитивной
Аддитивные и мультипликативные погрешности
Аддитивной погрешностью называется погрешность, постоянная в каждой точке шкалы.
Мультипликативной называется погрешность, линейно возрастающая или убывающая с ростом измеряемой величины.
Различать аддитивные и мультипликативные п. легче всего по полосе погрешностей.
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной п. (рис. а). Иногда такую п. называют погрешностью нуля. Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и п. называется мультипликативной (рис. б). Ярким примером аддитивной п. является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной п.
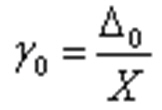
Для мультипликативной п.:
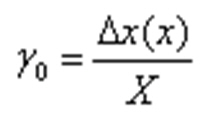
Абсолютная величина погрешности для обоих типов может быть выражена одной формулой:
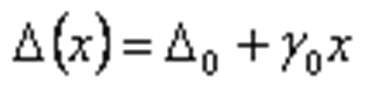
Относительная погрешность с учетом вышесказанного выражается:
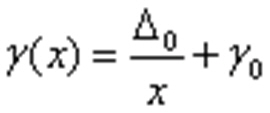
и, при уменьшении измеряемой величины, возрастает до бесконечности. Приведенное значение погрешности возрастает с увеличением измеряемой величины:
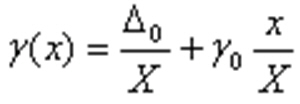
Какая погрешность называется аддитивной
Аналого-цифровые преобразователи (АЦП) являются важнейшим элементом современной вычислительной техники. Любой прибор, отображающий результаты измерений на цифровом табло (экране, индикаторе и т.п.), или осуществляющий их передачу по интерфейсам, или хранение в памяти ЭВМ, процессорного прибора или другого устройства цифровой (дискретной) техники, имеет в своем составе АЦП. Поэтому для нас так важна возможность ознакомиться с основными параметрами АЦП в нашем курсе метрологии.
Существуют общие определения, которые принято использовать в отношении аналого-цифровых преобразователей. Тем не менее, перечисляемые характеристики могут показаться довольно путаными. Правильный же выбор оптимального по сочетанию своих характеристик АЦП для конкретного приложения требует точного знания этих характеристик, более того, даже неспециалист может провести сравнение различных приборов или систем, опираясь на знание этих характеристик.
Наиболее часто путаемыми параметрами являются разрешающая способность и точность, хотя эти две характеристики реального АЦП крайне слабо связаны между собой. Разрешение не идентично точности, 12-разрядный АЦП может иметь меньшую точность, чем 8-разрядный. Для АЦП разрешение представляет собой меру того, на какое количество сегментов может быть поделен входной диапазон измеряемого аналогового сигнала (например, для 8-разрядного АЦП это 2 8 =256 сегментов). Точность же характеризует суммарное отклонение результата преобразования от своего идеального значения для данного входного напряжения. То есть, разрешающая способность характеризует потенциальные возможности АЦП, а совокупность точностных параметров определяет реализуемость такой потенциальной возможности.
Разрешение (разрядность) АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. Измеряется в битах. Например, АЦП, способный выдать 256 дискретных значений (0..255), имеет разрядность 8 бит, поскольку
Разрешение может быть также определено в терминах входного сигнала и выражено, например, в вольтах. Разрешение по напряжению равно напряжению, соответствующему максимальному выходному коду, деленному на количество выходных дискретных значений. Например:
Диапазон входных значений = от 0 до 10 вольт
Разрядность АЦП 12 бит: 2 12 = 4096 уровней квантования
Разрешение по напряжению: (10-0)/4096 = 0.00244 вольт = 2.44 мВ
Диапазон входных значений = от −10 до +10 вольт
Разрядность АЦП 14 бит: 2 14 = 16384 уровней квантования
Разрешение по напряжению: (10-(-10))/16384 = 20/16384 = 0.00122 вольт = 1.22 мВ
На практике разрешение и точность АЦП ограничены рядом причин. АЦП преобразует входной аналоговый сигнал в выходной цифровой код. Для реальных преобразователей, изготавливаемых в виде интегральных микросхем, процесс преобразования не является идеальным: на него оказывают влияние как технологический разброс параметров при производстве, так и различные внешние помехи. Поэтому цифровой код на выходе АЦП определяется с погрешностью. В спецификации на АЦП указываются погрешности, которые дает сам преобразователь. Их обычно делят на статические и динамические. При этом именно конечное приложение определяет, какие характеристики АЦП будут считаться определяющими, самыми важными в каждом конкретном случае.
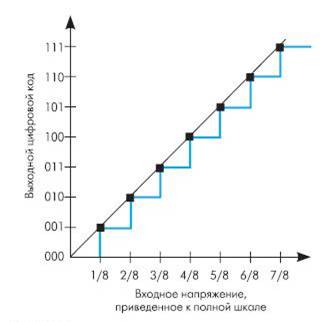
Идеальная передаточная характеристика АЦП
Рис. 1. Идеальная передаточная характеристика для 3-х разрядного АЦП
Из-за технологического разброса параметров при изготовлении интегральных микросхем реальные АЦП не имеют идеальной передаточной характеристики. Отклонения от идеальной передаточной характеристики определяют статическую погрешность АЦП и приводятся в технической документации.
Погрешности АЦП
В большинстве применений АЦП используют для измерения медленно изменяющегося, низкочастотного сигнала (например, от датчика температуры, давления, от тензодатчика и т.п.), когда входное напряжение пропорционально относительно постоянной физической величине. Здесь основную роль играет статическая погрешность измерения. В спецификации АЦП этот тип погрешности определяют аддитивная погрешность ( Offset ), мультипликативная погрешность ( Full-Scale ), дифференциальная нелинейность (DNL), интегральная нелинейность (INL) и погрешность квантования. Эти пять характеристик позволяют полностью описать статическую погрешность АЦП.
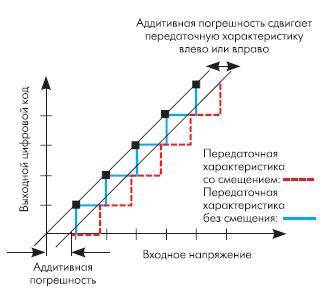
Аддитивная погрешность
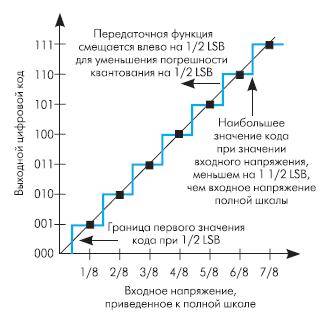
Идеальная передаточная характеристика АЦП пересекает начало координат, а первый переход кода происходит при достижении значения 1 LSB. Аддитивная погрешность (погрешность смещения) может быть определена как смещение всей передаточной характеристики влево или вправо относительно оси входного напряжения, как показано на рис.3. Таким образом, в определение аддитивной погрешности АЦП намеренно включено смещение 1/2 LSB.
Рис. 3. Аддитивная погрешность (погрешность смещения, Offset Error )
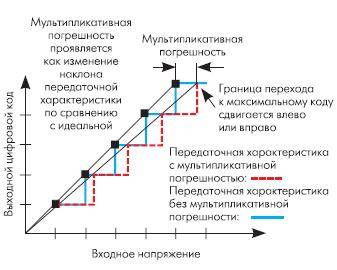
Мультипликативная погрешность
Мультипликативная погрешность (погрешность наклона) представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии нулевой аддитивной погрешности (т.е. смещение отсутствует). Это проявляется как изменение наклона передаточной функции, что иллюстрирует рис. 4.
Дифференциальная нелинейность
У идеальной передаточной характеристики АЦП ширина каждой «ступеньки» должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из 2 N «ступеней» представляет собой дифференциальную нелинейность (DNL).
Рис. 5. Д ифференциальная нелинейность (DNL).
Интегральная нелинейность, рассмотренная ниже, включает в себя DNL ошибки, поэтому DNL обычно не включается в список ключевых параметров АЦП. Нормально работающий АЦП — это никакого отсутствия или пропуска кода при подаче аналогового сигнала во всем диапазоне входного напряжения.
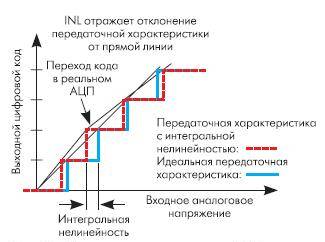
Интегральная нелинейность
Рис. 6. Интегральная нелинейность (INL)
Погрешность квантования
16.Аддитивная и мультипликативная погрешность.
Аддитивная погрешность– погрешность измерения которая при всех значениях входной измеряемой величины Х значения выходной величины Y изменяются на одну и ту же величину большую или меньшую от номинального значения.
Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений :
Мультипликативной погрешностью называется погрешность, линейно возрастающая или убывающая с ростом измеряемой величины.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной
Класс точности измерений :
— для мультипликативной погрешности: 
17.Погрешность квантования.
Разным значениям непрерывной измеряемой величины 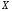



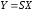
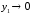
Значение 




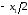
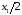
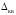
18.Понятие класса точности. Нормирование точности средств измерения.
Класс точности (КТ)— это обобщенная характеристика средства измерений, выражаемая пределами его допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.
Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности. Под ними понимают предельные для данного типа средства измерений погрешности.
Погрешность данного измерительного прибора не должна превосходить нормированного значения.
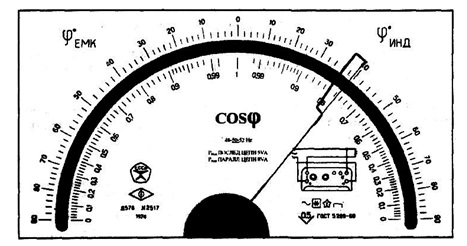
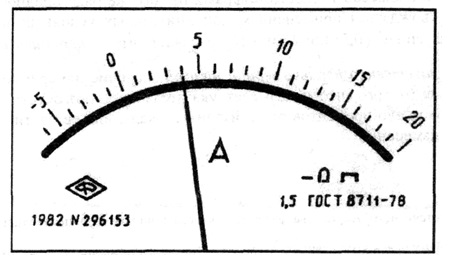
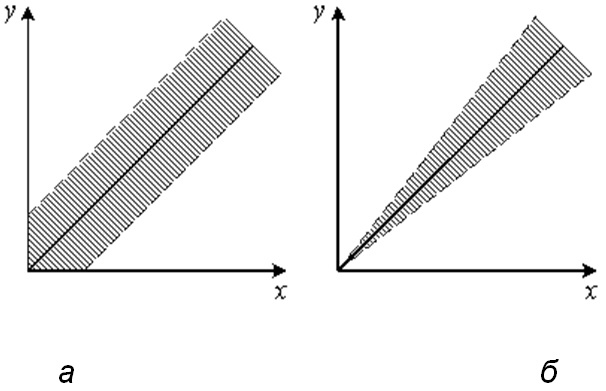
Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности γs=1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, шунтов, измерительных трансформаторов тока и напряжения и т. п.).
Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля γ о=0,5 %.
Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %.
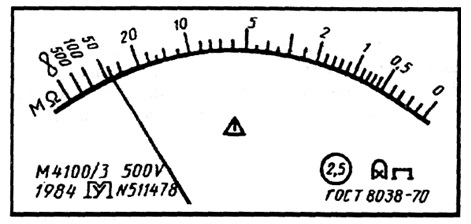
На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».
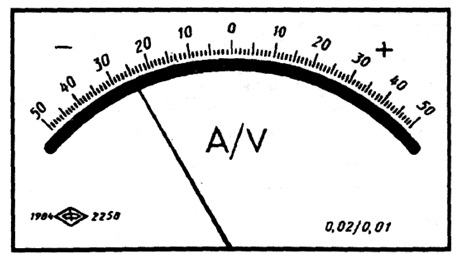
Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (например 0,02/0,01), это указывает на то, что приведенная погрешность в конце диапазона измерений γк = ±0,02 %, а в нуле диапазона γн = ±0,01 %. К таким измерительным приборам относятся высокоточные цифровые вольтметры, потенциометры постоянного тока и другие высокоточные приборы. В этом случае
Нормирование погрешностей средств измерений
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 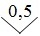
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
В том случае если абсолютная погрешность задается формулой 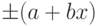
 | ( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: 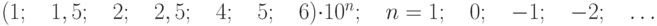
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Зависимость погрешностей от значения измеряемой величины Х.


— Если абсолютная погрешность измерительного прибора не зависит от измеряемой величины, то предел допускаемой основной погрешности может быть выражен одним числом
Такая погрешность называется аддитивной.
Примером может служить погрешность, связанная с неточной установкой нуля стрелочного прибора. Аддитивная погрешность постоянна во всем диапазоне измерений, в том числе и при Х=0, поэтому ее часто называют «погрешностью нуля«.
— Если погрешность прибора зависит от измеряемой величины, предел допускаемой погрешности выражается формулой

Таким образом, мультипликативная погрешность прямо пропорциональна значению Х. (см.рис.9).

Рис.9
Нормирование погрешности прибора.
Приведенная (нормированная) аддитивная погрешность может быть записана в виде

Приведенную (относительную) мультипликативную погрешность (с учетом и аддитивной погрешности) можно записать в общем виде 


1)
2)
3) 
4) 
Пример: Универсальный мост Е7-4 имеет основную относительную
погрешность при измерении (в %):
— сопротивления 
0,1 
10 
10 2 
1 
Поведение аддитивных и мультипликативных погрешностей с изменением измеряемой величины и их влияние на характеристику преобразования показано на рис.10
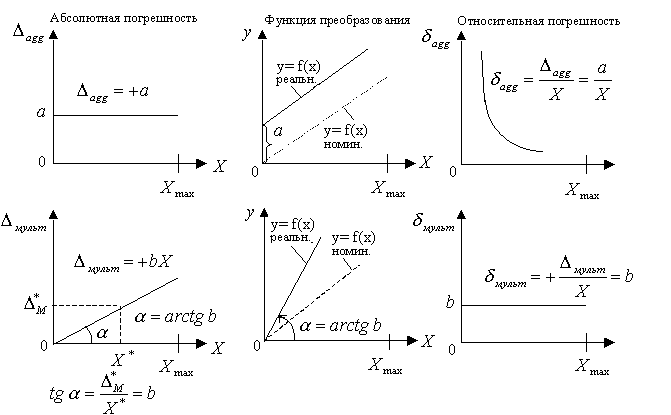
Рис.10
Формулы вида (27) и (28) используют при нормировании погрешностей средств измерения. Погрешности средств измерений при нормировании округляют до двух значащих цифр и выбирают равными ближайшему числу из следующего ряда: 1×10 n ; 1,5×10 n ; 2×10 n ; 2,5×10 n ; 4×10 n ; 5×10 n ; 6×10 n (n=1,0,-1,-2…).
Разработаны условные обозначения классов точности, которые применяются в документации, а также наносятся на шкалы средств измерения.
Класс точности совпадает со значением:
1. предельной (допускаемой) основной погрешности, выражаемой в процентах и округленной до ближайшего числа из указанного выше ряда.
Пример: обозначения классов точности Таблица 6.
| Форма выражения основной погрешности | Расчет допускаемой основной погрешности по формуле | Пределы допускаемой основной погрешности % | Обозначение класса точности на шкале прибора | |
| в доку-ментации | на приборе | |||
| Приведенная основная погрешность (предельная) | 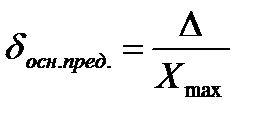 для СИ с равномерной шкалой- нормирование по пределу шкалы для СИ с неравномерной шкалой и нормирование производится по для СИ с равномерной шкалой- нормирование по пределу шкалы для СИ с неравномерной шкалой и нормирование производится по  длине шкалы. длине шкалы. | Примеры:  % %  % % | Класс точности 1,5 Класс точности 0,5 | В правой половине шкалы (как правило) 1,5 0,5 |
| Относительная основная погрешность |   |  % %  % % | Класс точности 0,5 Класс точности 0,02/0,01 | 0,5 0,02/0,01 |
| Абсолютная основная погрешность |   или по более сложной формуле или по более сложной формуле | Пример1, 2 (см. после таблицы 6). | Класс точности М | М |
Пример1. Пусть стрелочный (аналоговый) вольтметр имеет шкалу 0 
1) С какой абсолютной погрешностью можно измерить на этом приборе напряжение 220В?
а) Обозначение 1,0 означает основная приведенная предельная погрешность 
б) Предельная приведенная погрешность (по формуле (27))

в) Результат измерения
2) Какова относительная погрешность, если измерять 10В? 150?
Пример2. Цифровой вольтметр с классом точности 0,02/0,01 используется для измерения напряжения 220В на диапазоне 
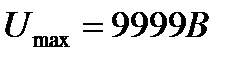
Основная относительная погрешность на этом диапазоне ( согласно формуле (28))
Вывод: на цифровых вольтметрах измерение выполняется с большей точностью.
3.3. Характеристики случайных погрешностей.
Составляющая погрешности измерения 
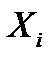

Эту разность называют случайной погрешностью отдельного измерения.
Истинное значение Х нам не известно. Однако, проведя большое количество измерений исследуемой величины Х, можно выявить следующие статистические закономерности (постулаты).
1. Если проводить серию измерений исследуемой величины и определить среднее арифметическое (среднее) значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов измерения от истинного значения величины в сторону уменьшения и увеличения (в том случае, когда систематическая погрешность равна нулю). Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического значения большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.
2. Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений. Эти статистические закономерности справедливы лишь при многократном повторении измерений ( 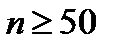


где n- число измерений. Тогда 
Указанные статистические закономерности большого числа измерений позволяют поставить вопрос о законе, по которому происходит распределение случайных погрешностей 
Аналитически он описывается выражением

где 

По своему смыслу плотность вероятности равна отношению вероятности (частоты) попадания случайной величины внутрь интервала 
Величину 

где 

Характер кривых, описываемых (33) показан на рис.11 для четырех значений 

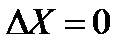



 |   |  |  | |||
 |  |  |   |  |  | |
| 0,4 | 0,4 | 0,6 | 0,8 | 0,14 | 1,2 | 0,01 |
| 0,5 | 0,5 | 0,49 | 1,0 | 0,11 | 1,5 | 0,0089 |
| 1,0 | 1,0 | 0,24 | 2,0 | 0,05 | 3,0 | 0,0045 |
| 2,0 | 2,0 | 0,12 | 4,0 | 0,03 | 6,0 | 0,0022 |
Как видно из рисунка, чем меньше 
Вероятность появления погрешности в пределах между (квантилями) 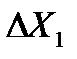



Рис.12
Эта функция получила название интегральной функции распределения.
В общем виде 
Вероятность того, что погрешность 



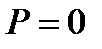
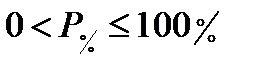
Интеграл (35) подстановкой

Интеграл (37) часто называют интегральной функцией ошибок или нормальным интегралом ошибок. Интеграл табулирован (представлен в таблице во многих справочниках, например, Бронштейн И.Н., Сомякуяев К.А. Справочник по математике, стр.81 1954г.).
На рис.13 его значения представлены графически
Таким образом, с вероятностью 0,683 случайные погрешности измерения не выходят за пределы 
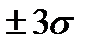
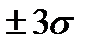
Считается, что появление погрешности равной 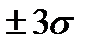
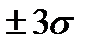
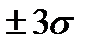
Соотношения (33) и (34) выведены из условия, что число измерений (одной и той же величины) 


Если вместо 




На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерений. Применение формулы (37) в этом случае дает заниженное значение доверительного интервала, т.е. оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнять доверительный интервал можно с помощью коэффициентов Стьюдента 


Для определения доверительного интервала среднюю квадратическую погрешность среднеарифметического ряда измерений надо умножить на коэффициент Стьюдента (квантиль).
Окончательный результат измерений можно записать так:

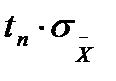
Таким образом последовательность статистической обработки результатов измерений при малом числе измерений (n 30…50) одной и той же величины.
Допустим, произведено n-число (n>30) измерений одной и той же величины одним и тем же оператором, на одном и том же оборудовании и в одних и тех же условиях (такие измерения называются равноточными).
а). Эти значения случайных величин

б). Этот вариационный ряд значений располагают в порядке возрастания величины слева направо
в). Весь диапазон полученных результатов измерений 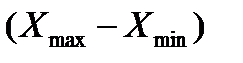
Ширина равномерных интервалов равна

Определим границы интервалов
Число интервалов r определяется числом измерений n и может быть выбрана на основании таблицы рекомендованной ВНИИМ