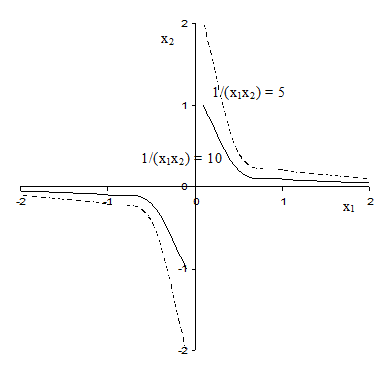какая поверхность называется графиком функции n переменных
Какая поверхность называется графиком функции n переменных
V . 1 . Дифференцируемость функции двух переменных
Функции двух переменных – частный случай функций нескольких (многих) переменных.
Пример 5.1. Найти область определения функции
Для функции двух (нескольких) переменных вводятся понятия предела функции, ее непрерывности и дифференцируемости в точке. Дадим понятие окрестности точки. δ-окрестностью точки M 0 ( x 0 ; y 0 ) называется совокупность всех внутренних точек круга радиуса δ с центром в точке M 0 или множество всех точек M ( x , y ) плоскости, координаты которых удовлетворяют неравенству 
Заметим, что для функции одной переменной стремление аргумента х к значению х0 возможно только по двум направлениям (справа и слева). Для функции двух переменных число таких направлений бесконечно, и если предел существует, то он не зависит от пути, по которому М стремится к М0.
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.
Заметим, что полное приращение не равно сумме частных приращений.
– она определена в этой точке и некоторой ее окрестности,
Пример 5.2. Найти частные производные по переменным функции
Сумма первых двух слагаемых последнего равенства для ∆ z представляет собой главную часть приращения и называется полным дифференциалом dz функции двух переменных. Таким образом
Каждое слагаемое правой части равенства (5.6) называется частным дифференциалом функции двух переменных по переменной х и у соответственно.
Функции нескольких переменных
| Главная > Учебные материалы > Математика: Функции нескольких переменных | ||
 | ||
 | ||
1.Основные понятия.
Многие явления и процессы в экономике, физике и других областях науки сложно изучить и объяснить с помощью функции от одной переменной. Поэтому в математике введен раздел и понятие функции нескольких переменных.
Например, площадь боковой поверхности конуса можно выразить в виде функции от двух переменных S = π R l.
Т.е. площадь есть функция от двух переменных S (R,l). Путь, пройденный за определенный промежуток времени с определенной скоростью, также можно выразить в виде функции от двух переменных S = vt т.е. S (v,t).
Если n = 2, то независимых переменных две и областью определения Х есть подмножество точек на координатной плоскости Оxy. Графиком функции от двух переменных называется совокупность точек в трехмерной системе координат с осями ОХ ОY и OZ.
Пример 1
Построить график функции z (x,y) = (5x)² + y².
Как видно из графика, в сечении поверхности z (x,y) = (5x)² + y² плоскостями Оzx, Ozy будут параболы. Например, если присвоить переменной x или y какое-либо фиксированное значение, то получим уравнения параболы.
При x=1 функция z = 25 + y². При y = 1, z = 25x² + 1.
Если отсечь поверхность плоскостью Оxy, то получим эллипс.
Пример 2
Если отсечь данную поверхность плоскостями Оzx, Ozy, то получим гиперболу, две части которой будут иметь общий максимум в точке х = 0 или y = 0. Т.е. если x или y примет какое-либо фиксированное значение, то функция примет вид:


Это объясняется тем, что левая часть равенства определена при любом значении х, если z > 1. И может быть не определена при определенном значении х, если z ≤ 1.
Построение графика функции от двух переменных является довольно сложной задачей. Поэтому для построения такого графика функции используют сечения в плоскостях Ozx, Ozy и Oxy.
Понятие функции нескольких переменных



Если каждой точке X = (х1, х2, …хn) из множества
Например, функция z = 1/(х1х2) представляет собой функцию двух переменных. Ее аргументы – переменные х1 и х2, а z – зависимая переменная. Область определения – вся координатная плоскость, за исключением прямых х1 = 0 и х2 = 0, т.е. без осей абсцисс и ординат. Подставив в функцию любую точку из области определения, по закону соответствия получим определенное число. Например, взяв точку (2; 5), т.е. х1 = 2, х2 = 5, получим
z = 1/(2*5) = 0,1 (т.е. z(2; 5) = 0,1).
Функция вида z = а1х1 + а2х2 + … + аnхn + b, где а1, а2,…, аn, b — по стоянные числа, называют линейной. Ее можно рассматривать как сумму n линейных функций от переменных х1, х2, …хn. Все остальные функции называют нелинейными.
Любой функции z = f (X) = f(х1, х2, …хn) можно поставить в соответствие n функций одной переменной, если зафиксировать значения всех переменных, кроме одной.
Графиком функции двух переменных z = f(x, у) называется множество точек трёхмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением
z = f (x, у). Этот график представляет собой некоторую поверхность в трехмерном пространстве (например, как на рисунке 5.3).
Можно доказать, что если функция – линейная (т.е. z = ax + by + c), то ее график представляет собой плоскость в трехмерном пространстве. Другие примеры трехмерных графиков рекомендуется изучить самостоятельно по учебнику Кремера (стр. 405-406).
Если переменных больше двух (n переменных), то графикфункции представляет собой множество точек (n+1)-мерного пространства, для которых координата хn+1 вычисляется в соответствии с заданным функциональным законом. Такой график называют гиперповерхностью (для линейной функции – гиперплоскостью), и он также представляет собой научную абстракцию (изобразить его невозможно).
Рисунок 5.3 – График функции двух переменных в трехмерном пространстве
Поверхностью уровня функции n переменных называется множество точек в n–мерном пространстве, таких, что во всех этих точках значение функции одно и то же и равно С. Само число С в этом случае называется уровнем.
Обычно для одной и той же функции можно построить бесконечно много поверхностей уровня (соответствующих различным уровням).
Для функции двух переменных поверхность уровня принимает вид линии уровня.
Например, рассмотрим z = 1/(х1х2). Возьмем С = 10, т.е. 1/(х1х2) = 10. Тогда х2 = 1/(10х1), т.е. на плоскости линия уровня примет вид, представленный на рисунке 5.4 сплошной линией. Взяв другой уровень, например, С = 5, получим линию уровня в виде графика функции х2 = 1/(5х1) (на рисунке 5.4 показана пунктиром).
Легко убедиться, что для линейной функции двух переменных любая линия уровня будет представлять собой прямую на плоскости, причем все линии уровня будут параллельны между собой.
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Помощь в дистанционном обучении
Решение тестов, помощь в закрытии сессии студентам МОИ, Синергии, ГТЕП, Витте, Педкампус, Росдистант
Математический анализ тест Синергии и МОИ
Тест Синергии и Московского Открытого Института «Математический анализ» Цена 200р.
Укажите область определения функции
Какая функция называется четной?
Выберите один ответ.
если для любых значений х из области определения
если для любых значений х из области определения
если для любых значений х из области определения
Какая из перечисленных функций не относится к алгебраическим функциям?
Выберите один ответ.
целая рациональная функция
В каком из перечисленных случаев величина называется параметром?
Выберите один ответ.
если она принимает различные значения
если она сохраняет постоянное значение лишь в условиях данного процесса
если она всегда сохраняет одно и то же значение
График какой функции симметричен относительно оси ординат?
Выберите один ответ.
функции общего вида
Выберите один ответ.
Относительно чего симметричен график нечетной функции?
Выберите один ответ.
относительно оси ординат
относительно оси абсцисс
относительно начала координат
Какая функция называется явной?
Выберите один ответ.
если функция задана уравнением F(х, у) = 0, не разрешенным относительно зависимой переменной
если функция задана формулой y = f(x), в которой правая часть не содержит зависимой переменной
если функция задана формулой y = f(x), в которой левая часть не содержит зависимой переменной
Укажите область определения функции
Выберите один ответ.
Выберите один ответ.
Укажите область определения функции
Выберите один ответ.
Какая из перечисленных функций не относится к трансцендентным функциям?
Выберите один ответ.
Выберите один ответ.
Какая поверхность называется графиком функции n переменных?
Выберите один ответ.
Какая функция у = f(x) называется возрастающей на промежутке X?
Выберите один ответ.
если большему значению аргумента из этого промежутка соответствует большее значение функции
если большему значению аргумента из этого промежутка соответствует меньшее значение функции
если большему значению аргумента из этого промежутка соответствует положительное значение функции
Выберите один ответ.
МОДУЛЬ 3. ДИФФЕРЕНЦИРОВАНИЕ
Найдите производную функции
Выберите один ответ.
Найдите производную функции f(t) = ln(2cos t)
Выберите один ответ
Выберите один ответ.
Найдите частные производные функции трех переменных
Выберите один ответ.
Чему, согласно правилу Лопиталя, равен предел отношения двух бесконечно малых или бесконечно больших функций, если последний существует?
Выберите один ответ.
пределу отношения производных двух бесконечно малых или бесконечно больших функций
пределу произведения производных двух бесконечно малых или бесконечно больших функций
пределу суммы производных двух бесконечно малых или бесконечно больших функций
Найдите частные производные второго порядка функции
Выберите один ответ.
Вычислите предел по правилу Лопиталя
Чему равна производная постоянной функции?
Укажите формулу для производной произведения функций u и v, если они дифференцируемы в некоторой точке, и их произведение также дифференцируемо в этой точке
Найдите частные производные функции двух переменных
Найдите полный дифференциал функции
Выберите один ответ.
dz = cosxy dx + 4xy dy
dz = — x cosxy dx + 2xy2
dz = (y cosxy + 2xy2) dx + (x cosxy + 2yx2) dy
dz = y cosxy dx + 2xy2dy
Найдите частные производные функции двух переменных z = xsin y + ysin x
Найдите частные производные второго порядка функции z = xy + xsin y
МОДУЛЬ 4. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Найдите точки максимума (минимума) функции
Выберите один ответ.
Найдите наибольшее и наименьшее значения функции на промежутке
Что называется асимптотой кривой?
Выберите один ответ.
прямая l, если расстояние от переменной точки М кривой до этой прямой стремится к единице при удалении точки М в бесконечность
прямая l, если расстояние от переменной точки М кривой до этой прямой стремится к бесконечности при удалении точки М в бесконечность
прямая l, если расстояние от переменной точки М кривой до этой прямой стремится к нулю при удалении точки М в бесконечность
Вертикальные асимптоты к графику функции имеют вид
Выберите один ответ.
Найдите наименьшее значение функции на отрезке [0; 3]
Выберите один ответ.
Найдите промежутки возрастания или убывания функции
Выберите один ответ.
возрастает при и убывает при
возрастает при и убывает при
убывает при и возрастает при
возрастает при и убывает при
Найдите точки максимума (минимума) функции
Выберите один ответ.
(2; 4) — точка минимума
(2; 4) — точка максимума
Определите поведение функции
Выберите один ответ.
Укажите необходимое условие экстремума
Выберите один ответ.
в точке экстремума функции ее производная всегда равна нулю (f'(x) = 0)
в точке экстремума функции ее производная не существует
в точке экстремума функции ее производная либо равна нулю (f'(x) = 0), либо не существует
Найдите точку перегиба кривой
Выберите один ответ.
Что называется критическими точками второго рода?
Выберите один ответ.
точки области определения, в которых вторая производная функции y = f(x) обращается в нуль или не существует
точки области определения, в которых первая производная функции y = f(x) обращается в нуль или не существует
точки области определения, в которых производная функции y = f(x) равна единице
Найдите промежутки возрастания или убывания функции
Выберите один ответ.
Найдите точки максимума (минимума) функции
Выберите один ответ.
— точка минимума, (1; 0,5) — точка максимума
— точка минимума, (0,5; 10,5) — точка максимума
— точка минимума, (1; 0,5) — точка максимума
Найдите промежутки возрастания или убывания функции
Выберите один ответ.
убывает при x > 2, возрастает x 2
Каково необходимое условие возрастания функции?
Выберите один ответ.
если функция y = f(x) дифференцируема и возрастает на интервале (a; b), то для всех x из этого интервала
если функция y = f(x) дифференцируема и возрастает на интервале (a; b), то для всех x из этого интервала
если функция y = f(x) дифференцируема и возрастает на интервале (a; b), то для всех x из этого интервала
Какая кривая y = f(x) называется выпуклой на интервале (a, b)?
Выберите один ответ.
если все точки кривой лежат на ее касательной на этом интервале
если все точки кривой лежат ниже любой ее касательной на этом интервале
если все точки кривой лежат выше любой ее касательной на этом интервале
Найдите вертикальные асимптоты к графику функции
Выберите один ответ.
В каких точках выпукла или вогнута кривая
Выберите один ответ.
выпукла во всех точках
вогнута во всех точках
Определите поведение функции при x = 0
Выберите один ответ.
Число называется наибольшим значением функции на отрезке [a; b], если
Выберите один ответ.
для всех x из этого отрезка выполняется неравенство
для всех x из этого отрезка выполняется неравенство
для всех x из этого отрезка выполняется неравенство
В каких точках выпукла или вогнута кривая
Выберите один ответ.
выпукла во всех точках
вогнута во всех точках
Найдите точку перегиба кривой
Выберите один ответ.
Исследуйте функцию на экстремумы
Выберите один ответ.
максимум в точке 2; минимум в точке 0
максимум в точке 0; минимум в точке
максимум в точке ; минимум в точке 0
Определите поведение функции
Выберите один ответ.
Исследуйте функцию на монотонность и экстремум
Выберите один ответ.
— промежуток убывания, — промежуток возрастания, x = 0 — точка минимума
возрастает на всей числовой прямой
— промежуток возрастания, — промежуток убывания, x = 2 — точка максимума
— промежуток возрастания, — промежуток убывания, x = 0 — точка максимума
МОДУЛЬ 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Найдите первообразную для функции
Чему равен неопределенный интеграл от алгебраической суммы функций?
Выберите один ответ.
алгебраической сумме интегралов от этих функций
алгебраическому произведению интегралов от этих функций
алгебраической разности интегралов от этих функций
Сколько первообразных может иметь каждая функция?
Выберите один ответ.
бесконечно много первообразных
Укажите формулу интегрирования по частям
МОДУЛЬ 6. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Вычислите определенный интеграл
Укажите какая из сумм является интегральной
МОДУЛЬ 7. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Вычислите площадь плоской фигуры, ограниченной линиями: и y = 0
Найдите площадь области, ограниченной прямыми и осью Ox
Найдите площадь фигуры, заключенной между прямыми и осью Ox
Сила в 6 кГ растягивает пружину на 8 см. Какую работу она производит?
Выберите один ответ.
Какую работу совершает сила в 8 H при растяжении пружины на 6 см?
Выберите один ответ.
Выберите один ответ.
Выберите один ответ.
Вычислите силу давления воды на стенку шлюза, длина которого 20 м и высота 5 м, считая шлюз доверху заполненным водой
Выберите один ответ.
Тело движется прямолинейно со скоростью м/с. Найдите путь, пройденный точкой за первые 5 с от начала движения
Выберите один ответ.
Найдите площадь фигуры, ограниченной прямыми y = 4x, x = 4 и осью Ox
Выберите один ответ.
Выберите один ответ.
Найдите площадь фигуры, ограниченной линиями
Выберите один ответ.
Выберите один ответ.
Выберите один ответ.
Вычислите силу давления воды на одну из стенок аквариума имеющего длину 30 см и высоту 20 см
Выберите один ответ.
Найдите площадь фигуры, ограниченной прямыми y = 5x, x = 2 и осью Ox
Выберите один ответ.
Найдите площадь фигуры, ограниченной параболами:
Выберите один ответ.
Найдите площадь фигуры, ограниченной отрезком оси Ox, графиком функции y = cosx, отрезками прямых и x = π
Скорость падающего в пустоте тела определяется по формуле v = 9,8t м/сек. Какой путь пройдет тело за первые 10 секунд падения?
Выберите один ответ.
Выберите один ответ.
Найдите площадь фигуры, ограниченной линиями
Выберите один ответ.
МОДУЛЬ 8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Что называется порядком дифференциального уравнения?
Выберите один ответ.
наивысший порядок второй производной, входящей в дифференциальное уравнение
наивысший порядок переменной, входящей в дифференциальное уравнение
наивысший порядок производной, входящей в дифференциальное уравнение
Даны дифференциальные уравнения: 1. 2. 3. 4. 5. 6. Укажите среди них однородные уравнения
Выберите один ответ.
Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?
Выберите один ответ.
Найдите частное решение уравнения 2(z + 3)dt = (t + 2)dz, если при
Выберите один ответ.
Найдите общее решение уравнения y′′ = cos x
Найдите общее решение уравнения y′ = sin x + 2
Выберите один ответ.
y = cosx + 2x + C1х + С2
Какое уравнение называется дифференциальным уравнением?
Выберите один ответ.
уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков
уравнение, содержащее функцию от независимой переменной и ее производные различных порядков
уравнение, содержащее независимую переменную и функцию от этой независимой переменной
Среди перечисленных уравнений укажите однородные уравнения: 1. ; 2. ; 3. ; 4. ; 5. ; 6.
Выберите один ответ.
Найдите частное решение уравнения 2sdt = tds, если при t = 1 s = 2
Выберите один ответ.
Найдите общее решение уравнения
Выберите один ответ.
Среди перечисленных дифференциальных уравнений укажите уравнение с разделяющимися переменными
Укажите общее решение дифференциального уравнения
Найдите общее решение уравнения (3x + 2)dy + (y + 2)dx = 0
Среди перечисленных дифференциальных уравнений укажите уравнения с разделяющимися переменными: 1. ; 2. ; 3. 4. 5. ; 6.
Выберите один ответ.
Среди перечисленных дифференциальных уравнений укажите уравнение с разделяющимися переменными
Выберите один ответ.
Среди перечисленных дифференциальных уравнений укажите однородное уравнение
Найдите общее решение уравнения (x + y)dx + xdy = 0
Найдите частное решение уравнения xdx = dy, если при x = 1 y = 0
МОДУЛЬ 9. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Среди перечисленных дифференциальных уравнений указать уравнение Бернулли: 1. ; 2. ; 3. ; 4.
Выберите один ответ.
Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли
Найдите частное решение дифференциального уравнения y′ + 4y = 2, удовлетворяющее начальному условию y(0) = 6
Даны дифференциальные уравнения: 1. 2. 3. 4. Укажите среди них линейные уравнения
Выберите один ответ.
Выберите один ответ.
при решении однородных уравнений
при решении уравнений с разделяющими переменными
при решении линейных уравнений
Среди перечисленных дифференциальных уравнений укажите линейное уравнение
Выберите один ответ.
Среди перечисленных уравнений укажите линейные уравнения первого порядка: 1. ; 2. ; 3. ; 4.
Выберите один ответ.
Укажите частное решение дифференциального уравнения y′ + 2y = 4 удовлетворяющее начальному условию y(0) = 5
Какую подстановку используют при решении уравнений Бернулли?
Выберите один ответ.
Найдите радиус сходимости ряда
Выберите один ответ.
Исследуйте сходимость ряда
Выберите один ответ.
Укажите необходимый признак сходимости ряда
Выберите один ответ.
eсли ряд сходится, то его n-й член стремится к нулю при
eсли ряд сходится, то его n-й член стремится к нулю при
eсли ряд сходится, то его n-й член стремится к бесконечности при
Какой ряд называется знакопеременным рядом?
Выберите один ответ.
числовой ряд, члены которого имеют различные знаки
числовой ряд, у которого соседние члены имеют противоположные знаки
- Низкоуглеводное топливо что это
- Некоторые сорта картофеля сильно развариваются пропитываются водой в результате чего вкус