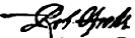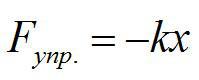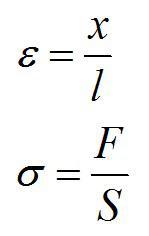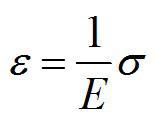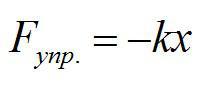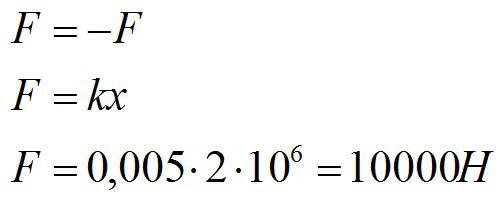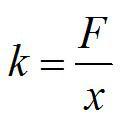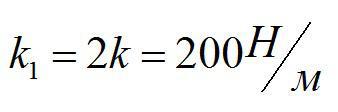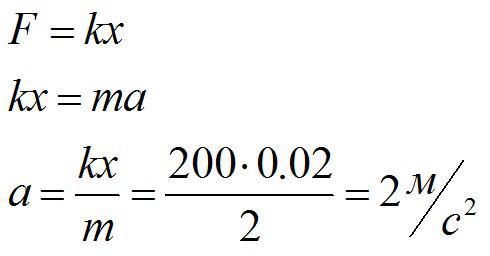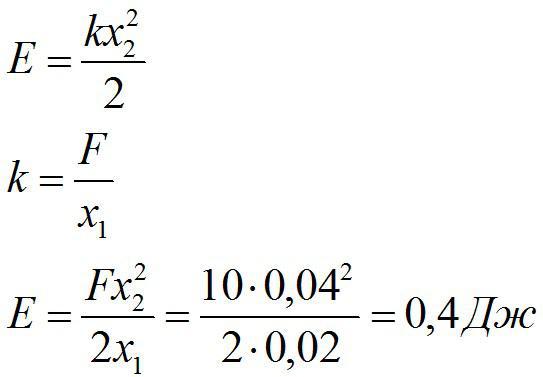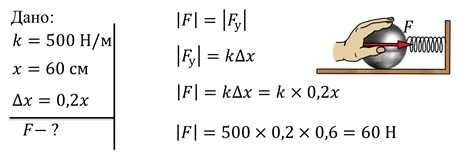какая пружина стальная или медная при упругой деформации под действием

Учебники

Журнал «Квант»

Общие

А так ли хорошо знакомы вам деформации? // Квант. — 1994. — № 3. — С. 32-33.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

. сила любой пружины пропорциональна ее растяжению.

Содержание

Конечно же, в утверждении Гука речь идет об одной из самых наглядных — об упругой деформации. Однако в школе дается представление и о других видах деформаций, изучение которых играет огромную роль. Вспомните задачи об упругих и неупругих ударах, о равновесии тел, об изменении формы и объема тел, о механических колебаниях… Список настолько велик, а понимание связанных с деформациями механических свойств тел столь важно для науки и техники, что можно без преувеличения говорить об исследовании этих свойств как об одной из главных задач современной физики.

Получается, что и в школьном курсе к понятию деформации приходится обращаться не раз и в различных его частях. На макроскопическом уровне — в механике и при изучении тепловых явлений; при объяснении взаимодействия атомов и молекул — в кинетической теории вещества; при выявлении природы упругих сил — в электромагнетизме. Поэтому так разнообразны ситуации, в которых вы сегодня встретитесь с этим отнюдь не второстепенным понятием.

Вопросы и задачи

Микроопыт

Поставьте вертикально резиновую трубку, на которую предварительно туго надето металлическое кольцо, и растяните трубку. Что при этом произойдет с кольцом? Почему?

Любопытно, что.

. научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенсом, Ньютоном и др.). Однако «закон Гука» был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался.

. в начале XVIII века участились аварии на рудниках, связанные с разрывом железных цепей, применяемых в шахтных подъемниках. Попытки модернизировать цепи предпринимали многое ученые, в том числе и знаменитый математик и философ Г.Лейбниц. Но — безуспешно. А вот старшему горному советнику, юристу по образованию, В. Альберту пришла в голову идея заменить цепи проволочными канатами или тросами. Это позволило использовать такое важное свойство железа, как прочность на растяжение.

. побеление мокрого песка при ходьбе по нему впервые удалось объяснить в 1885 году английскому физику и инженеру О.Рейнольдсу. Он показал, что под действием возникающей под ногой деформации сдвига объем, занимаемый песчинками, увеличивается и песок некоторое время находится выше уровня воды.

. одиночные кристаллы многих металлов, выросшие из расплава, оказываются настолько мягкими, что их легко согнуть пальцами. А вот разогнуть — уже не удается. Это — пример замечательной способности пластически деформируемых тел упрочняться.

. объяснение пластической деформации возникло лишь тогда, когда физики (уже в нашем столетии) открыли так называемые дислокации — дефекты кристаллической решетки твердого тела. С современной точки зрения, этот вид деформации есть «движение беспорядка» вдоль кристалла.

. на сегодняшний день получены особые сверхупругие сплавы, напоминающие поведением резину и способные выдерживать огромные упругие деформации — на два порядка больше, чем обычные металлы. С другой стороны, многие сплавы можно привести в сверхпластичное состояние, когда они при очень низких напряжениях текут, подобно разогретому стеклу.

. совместить противоположные механические характеристики удается в композитах — «сборных» материалах, включающих легкую и пластичную основу и наполнители из тонких волокон очень прочного вещества.

. можно измерить деформации, меньшие диаметра атома, правда, если они носят колебательный характер — тогда их легко преобразовать в электрические сигналы. Кстати, ухо человека способно «измерить» столь же малые деформации барабанной перепонки.

. при деформации кварца и некоторых других диэлектриков на их поверхности возникают электрические заряды, а поляризация диэлектриков в электрическом поле может привести к их деформации. Эти явления называют прямым и обратным пьезоэлектрическим эффектом.

. если достаточно долго облучать свинец нейтронами, в нем происходит внутренняя перестройка и он становится настолько упругим, что изготовленный из него колокол мог бы звучать не хуже отлитых из лучшей колокольной бронзы.

Что читать в «Кванте» о деформациях

(публикации последних лет)

Ответы

Микроопыт

Поскольку при растяжении трубки уменьшается диаметр ее поперечного сечения, кольцо упадет вниз.

Источник

Сила упругости

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_<0>\) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

\[ \large L_ <0>+ \Delta L = L \]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_<0>\).

\( L_ <0>\left(\text <м>\right) \) – начальная длина пружины;

\( L \left(\text <м>\right) \) – конечная длина растянутой пружины;

\( \Delta L \left(\text <м>\right) \) – кусочек длины, на который растянули пружину;

Величину \( \Delta L \) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_<\text<упр>> \) силой упругости.

\[ \large \boxed< F_<\text<упр>> = k \cdot \Delta L >\]

Эту формулу назвали законом упругости Гука.

\( F_<\text<упр>> \left( H \right) \) – сила упругости;

\( \Delta L \left(\text <м>\right) \) – удлинение пружины;

\( \displaystyle k \left(\frac<\text<м>> \right) \) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

\[ \large F_<\text<упр>> — m \cdot g = 0 \]

Подставим в это уравнение выражение для силы упругости

\[ \large k \cdot \Delta L — m \cdot g = 0 \]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину \(\Delta L\). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом \(mg\).

\[ \large k_ <1>\cdot \Delta L = m \cdot g \]

Две параллельные пружины:

\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= k_ <1>\cdot \Delta L \]

Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:

Умножим обе части полученного уравнения на число 2:

Коэффициент жесткости \(k_<\text<параллел>>\) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину \(\Delta L\). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину \(\Delta L\).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом \(mg\).

\[ \large k_ <1>\cdot \Delta L = m \cdot g \]

Две последовательные пружины:

\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = k_ <1>\cdot \Delta L \]

Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:

Разделим обе части полученного уравнения на число 2:

Коэффициент жесткости \(k_<\text<послед>>\) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину \(\Delta L \) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

\[ \large \boxed < E_

= \frac <2>\cdot \left( \Delta L \right)^ <2>>\]

\( E_

\left( \text <Дж>\right)\) – потенциальная энергия сжатой или растянутой пружины;

\( \Delta L \left(\text <м>\right) \) – удлинение пружины;

\( \displaystyle k \left(\frac<\text<м>> \right) \) – коэффициент жесткости (упругости) пружины.

Источник

Задачи на тему «Сила упругости. Закон Гука» с решениями

Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.

Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.

Сила упругости и закон Гука: определения

Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.

Примеры действия силы упругости:

Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.

Коэффициент k – жесткость материала.

Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:

S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.

Здесь Е – модуль Юнга, зависящий от свойств материала.

Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.

Вопросы на силу упругости и закон Гука

Вопрос 1. Какие бывают деформации?

Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.

Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?

Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.

Вопрос 3. Как направлена сила упругости?

Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.

Вопрос 4. Какую природу имеет сила упругости?

Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.

Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?

Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.

Задачи на силу упругости и закон Гука с решениями

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задача №1. Расчет силы упругости

Условие

Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.

Решение

Запишем закон Гука:

По третьему закону Ньютона:

Ответ: 10 кН.

Задача №2. Нахождение жесткости пружины

Условие

Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?

Решение

По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.

Ответ: 200 Н/м

При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.

Задача №3. Нахождение ускорения тела

Условие

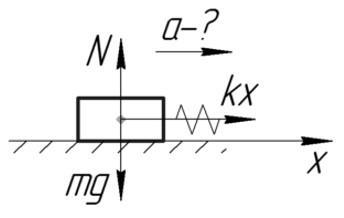
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.

Решение

За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:

Ответ: 2 м/с^2.

Задача №4. Нахождение жесткости пружины по графику

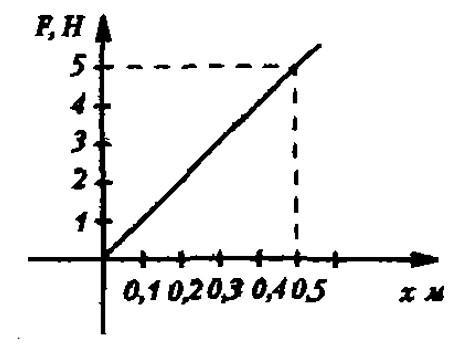
Условие

На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.

Решение

Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.

Ответ: k=10 Н/м.

Задача №5. Определение энергии деформации

Условие

Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.

Решение

Энергия сжатой пружины равна:

Ответ: 0,4 Дж.

Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.

Источник

Деформация и силы упрогости. Закон Гука

Урок 20. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Деформация и силы упрогости. Закон Гука»

Силы упругости возникают только при деформации тел и исчезают, когда деформация прекращается.

Деформация — это изменение объёма или формы тела.

Хорошо известно, что, для того чтобы сжать или растянуть пружину, необходимо приложить некоторую силу.

Потому что, когда вы деформируете пружину, в ней возникают силы упругости, действующие на ваши руки.

При любом виде деформации, действуют силы упругости, которые стремятся вернуть тело к исходной форме. Как только тело возвращается в исходную форму, деформация прекращается, и силы упругости пропадают. При деформации, различные части тела совершают различные перемещения.

Существует четыре типа деформаций: изгиб, сжатие, растяжение и кручение.

Силы упругости также возникают и при попытке деформировать тело. Например, при ударе по наковальне, возможно, вам не хватит силы, чтобы её деформировать.

Это значит, что силы упругости наковальни, воспрепятствовали деформации.

Как вы знаете, жидкости и газы не сохраняют форму, поэтому силы упругости в них не возникают при попытке деформации. Мы перелить воду из одной ёмкости в другую, но это не вызовет сил упругости. Зато если мы поместим воду в пластиковую бутылку и попытаемся её сжать, то сможем явно ощутить сопротивление в результате возникновения сил упругости. То же самое можно сказать и о газах: если мы попытаемся сжать воздушный шарик, то тоже встретим сопротивление.

Существуют упругие и неупругие деформации.

При неупругой деформации, тело не восстанавливает свою исходную форму. Например, если достаточно сильно ударить молотком по монете, то она деформируется, и уже никогда не восстановит свою первоначальную форму.

При упругой деформации тело восстанавливает исходные размеры и форму сразу после прекращения действия сил, вызвавших деформацию. Примером упругой деформации может послужить отскок мяча от пола. При ударе о пол, нижняя часть мяча резко останавливается, в то время как верхняя часть мяча всё еще двигается по инерции. То есть, при этом, различные части мяча совершают различные перемещения. В результате, мы видим, как мяч на короткое время сплющивается. Но как только он перестаёт взаимодействовать с полом, его форма восстанавливается.

Очевидно, что чем больше деформация, тем больше силы упругости, возникающие в теле.

Связь силы упругости тела с мерой его деформации была открыта Робертом Гуком. В своих экспериментах, он установил следующее: при упругой деформации растяжения или сжатия, удлинение тела прямо пропорционально приложенной силе. Математически этот закон записывается просто: .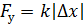

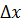
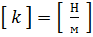
Обратите внимание, что мы записали закон не в векторной форме. — это изменение длины тела, а k — это коэффициент упругости или коэффициент жёсткости. Исходя из формулы, легко понять, что жёсткость измеряется в ньютонах на метр: .

Для каждого материала, коэффициент жёсткости определяется экспериментально.

Силы упругости всегда препятствуют деформации. Поэтому проекция силы упругости на ось х отрицательная, поскольку ось х направлена в противоположную сторону, чем сила упругости.

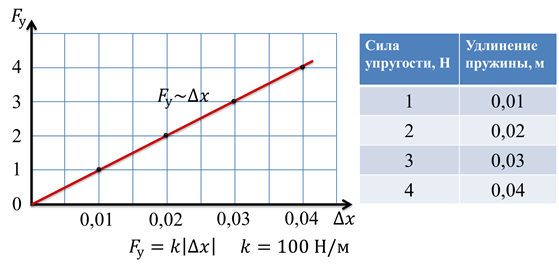
Графиком зависимости силы упругости от удлинения пружины является прямая линия.

Это говорит о том, что сила упругости, возникающая при упругой деформации прямо пропорциональна удлинению тела. Коэффициентом пропорциональности в этой зависимости является коэффициент жесткости.

Необходимо отметить, что закон Гука выполняется только при упругих деформациях, когда изменение длины тела невелико по сравнению с его размерами.

Примеры решения задач.

Задача 1. Какую силу нужно приложить к пружине с коэффициентом жёсткости 500 Н/м, чтобы сжать её на 20%? Длина пружины составляет 60 см.

Задача 2. Рыбак вытягивает рыбу из воды вертикально вверх с ускорением 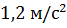. Масса рыбы равна 1,5 кг, а коэффициент жесткости лески составляет 800 Н/м. Найдите растяжение лески.

Как мы помним, если подвес двигается с ускорением вверх, то тело будет испытывать перегрузку. Напомним, что при этом вес тела не равен силе тяжести.

Источник