какая разница между теплоемкостью тела и удельной теплоемкостью

Какова разница между теплоемкостью тела и удельной теплоемкостью?

Какова разница между теплоемкостью тела и удельной теплоемкостью.

Что такое удельная теплоемкость вещества?

Что такое удельная теплоемкость вещества?

Два тела равной массы и разной удельной теплоемкости имеют одинаковую температуру?

Два тела равной массы и разной удельной теплоемкости имеют одинаковую температуру.

Если нагреть на 100º тело большей теплоемкости и привести его в тепловой контакт с телом меньшей теплоемкости, то установившаяся температура окажется на 10º больше, чем в случае, когда на 100º нагревают менее теплоемкое тело и затем приводят в контакт с более теплоемким.

Найти отношение удельных теплоемкостей тел.

Удельной теплоемкостью вещества называют?

Удельной теплоемкостью вещества называют.

Что показывает удельная теплоемкость?

Что показывает удельная теплоемкость?

Удельная теплоемкость металла?

Удельная теплоемкость металла?

Что называется удельной теплоемкостью?

Что называется удельной теплоемкостью?

Удельная теплоемкость зависит от?

Удельная теплоемкость зависит от?

Лабораторная работа по физике Измерение удельной теплоемкости твердого тела?

Лабораторная работа по физике Измерение удельной теплоемкости твердого тела.

Каков физический смысл теплоемкости тела и удельной теплоемкости вещества?

Каков физический смысл теплоемкости тела и удельной теплоемкости вещества?

Как зависит быстрота нагревания разных тел одинаковой массы от удельной теплоемкости?

Как зависит быстрота нагревания разных тел одинаковой массы от удельной теплоемкости?

Полив необходим растениям для роста и развития : вода растворяет питательные вещества в земле и по корням, стебль доставляет их по всему растению ; сохраняет тонус растения, предохраняет от засыхания.

E = F / q = 300 * 10⁻⁶ Н / 3 * 10⁻⁹ Кл = 1 * 10⁵ Н / Кл E = k * Q / r² = > Q = E * r² / k Q = 1 * 10⁵ Н / Кл * (0, 10 м)² / 9 * 10⁹ Н * м² / кл² = 1, 1 * 10⁻⁷ Кл = 0, 11 мкКл.

Тому сила струму зменшуэться.

710ПА 22000ПА 150000ПА ПОСЛЕДНИЕ ХЗ.

Каким прибором? Вы не сказали.

Источник

Количество теплоты и удельная теплоемкость

Вместо словосочетания «тепловая энергия» физики говорят сокращенно: «теплота».

Удобно сравнивать между собой величины, которые измерены численно. Поэтому, физики говорят о количестве тепловой энергии, или количестве теплоты.

Что такое количество теплоты

Рассмотрим чашку, в которой находится обыкновенная вода комнатной температуры.

Вычислим внутреннюю энергию холодной воды в чашке, получим число, которое можно обозначить так:

\(\large U_<\text<хол>> \left( \text <Дж>\right) \) – внутренняя энергия холодной воды.

Нагреем воду в чашке. Молекулы нагретой воды будут двигаться быстрее. Значит, горячая вода обладает большим количеством внутренней энергии.

Теперь посчитаем внутреннюю энергию горячей воды в чашке. Полученное число обозначим, как

\(\large U_<\text<горяч>> \left( \text <Дж>\right) \) – внутренняя энергия горячей воды.

Найдем разницу внутренней энергии для горячей и холодной воды.

Примечание: Вместо слова «разница» математики скажут «разность».

Мы получим еще одно число. Обозначим его символом Q. Число Q называют количеством теплоты. Именно эту тепловую энергию вода получила во время нагревания.

Примечание: Когда горячая вода остынет, она отдаст ровно столько тепловой энергии, сколько получила во время нагревания. Потому, что выполняется закон сохранения тепловой энергии.

\(\large Q \left( \text <Дж>\right) \) – тепловая энергия, количество теплоты.

Теплота, как и любая энергия, измеряется в системе СИ в Джоулях, в честь английского физика Джеймса Джоуля.

Примечание: Количество теплоты, так же, измеряют в Калориях.

Калория – это тепловая энергия, затраченная на нагревание 1 грамма воды на 1 градус Цельсия.

Джоуль и Калория связаны так:

От чего зависит количество теплоты

Количество теплоты, требуемое для нагревания тела, зависит от нескольких параметров.

От массы вещества

Нальем в одну кастрюльку 1 кг воды, а в другую, точно такую же кастрюльку – 2 килограмма воды.

Пусть, начальная температура воды о обеих кастрюльках равна +20 градусам Цельсия.

Будем нагревать эти кастрюльки по очереди на газовой плите, не меняя интенсивность огня конфорки.

Предположим, нам нужно повысить на 50 градусов Цельсия температуру воды в каждой кастрюльке.

Примечание: После нагревания воды на 50 градусов, конечная температура воды в каждой кастрюльке будет равна 70 градусам.

Чтобы нагреть на 50 градусов 1 килограмм воды, потребуется время. Однако, чтобы нагреть на этой же конфорке 2 килограмма воды на 50 градусов, потребуется больше времени.

Значит, количество теплоты, полученное водой, зависит от массы вещества, которое мы хотим нагреть.

Математики запишут фразу «количество теплоты зависит от массы» так:

Символом f обозначается зависимость.

\(\large m \left( \text <кг>\right) \) – масса нагреваемого вещества.

От разницы температур

Теперь возьмем две кастрюльки, и нальем в них по 1 кг воды. Начальная температура воды в кастрюльках одинаковая и равна +20 градусов Цельсия.

Одну кастрюльку будем нагревать дольше другой. Поэтому, температура воды будет выше в той кастрюльке, которую дольше нагревали.

Так как температура повысилась больше в кастрюльке, которую дольше нагревали, то физики скажут, что воде в этой кастрюльке передали большее количество теплоты.

Значит, количество теплоты зависит от разницы (т. е. разности) между начальной и конечной температурой.

\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;

\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;

\(\large \Delta t \left( \text <град>\right) \) – разность температуры;

Математики фразу «количество теплоты зависит от разности температур» запишут так:

Символ f обозначает, что Q зависит от разницы температур.

От вида вещества

Теперь будем нагревать 1 килограмм воды и 1 килограмм подсолнечного масла.

Первоначальная температура каждого вещества +20 градусов Цельсия.

Измерим через 5 минут нагревания температуру воды и температуру масла.

Оказывается, за 5 минут масло нагреется до более высокой температуры. При этом и масло, и вода, получили одинаковое количество теплоты.

Значит, количество теплоты зависит от того, из какого вещества состоит тело.

Какие величины называют удельными

Физики часто применяют удельные величины, так как они достаточно удобны для вычислений.

Удельная величина – величина, приходящаяся на единицу массы, длины, площади, или объема.

В обычной жизни мы, так же, пользуемся удельными величинами. К примеру, цена товара – это удельная величина, так как она приходится на единицу товара. Зная количество товара, легко посчитать общую цену покупки.

Например, булочка стоит 20 рублей. Нужно купить 3 булочки. Общую сумму денег найдем, перемножив цену одной булочки (удельную величину) на количество штук.

Известно, что при горении топлива выделяется энергия. Удельная теплота сгорания и количество сгоревших килограммов топлива помогут посчитать выделившуюся тепловую энергию.

Что такое удельная теплоемкость

Возьмем 1 килограмм вещества и нагреем его на 1 градус Цельсия. Тепловая энергия, которую мы для этого затратили, называется удельной теплоемкостью.

Удельная теплоемкость – это энергия, затраченная для нагревания 1 килограмма на 1 градус.

Эту энергию обозначают латинским символом «c». Измеряют ее в Джоулях, деленных на килограмм и градус.

\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;

Примечания:

Удельные теплоемкости воды в различных агрегатных состояниях

В твердом состоянии (лед), вода будет иметь такую теплоемкость:

В жидком состоянии (вода), такую:

В газообразном состоянии (пар) при температуре 100 градусов Цельсия, такую:

Примечание: Удельные теплоемкости различных веществ можно найти в школьном справочнике физики.

Как связаны и чем отличаются количество теплоты и удельная теплоемкость

Будем рассматривать такие процессы, как нагревание и охлаждение.

Благодаря процессам нагревания и охлаждения мы можем обогреваться зимой с помощью русской печи. Сначала печь получит количество теплоты (тепловую энергию) от сгорающего топлива — дров. А затем, будет остывать и отдавать это количество теплоты всем телам, находящимся в помещении.

Отличия удельной теплоемкости от количества теплоты

Запомнить, что такое количество теплоты, и чем оно отличается от удельной теплоемкости, можно так (рис. ):

Связь количества теплоты и удельной теплоемкости — формула

то легко посчитать общую тепловую энергию – т. е. количество теплоты.

Для этого используем формулу:

\(\large Q \left( \text <Дж>\right) \) – количество теплоты, т. е. общая тепловая энергия;

\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;

\(\large m \left( \text <кг>\right) \) – масса вещества;

\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;

\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;

Как по графику нагревания или охлаждения определить удельную теплоемкость

На примере покажем, как находить удельную теплоемкость по графику нагревания или охлаждения тела.

Дано твердое тело массой 2 килограмма. На рисунке 5 указано, как зависит температура этого тела от полученного количества теплоты. По горизонтали отложено количество теплоты, а по вертикали – температура некоторого тела, находящегося в твердом состоянии.

Определить удельную теплоемкость вещества, из которого состоит данное твердое тело.

Решение:

Тело нагрелось от \(\large t_ <1>= 0 \left( С \right) \) до температуры \(\large t_ <2>= 60 \left( С \right) \);

Разность температур равна 60 градусам Цельсия.

Масса тела 2 килограмма.

Полученное количество теплоты \(\large Q = 15000 \left( \text <Дж>\right) \).

Выпишем формулу, по которой можно посчитать тепловую энергию Q:

Подставим теперь значения в эту формулу для определения количества теплоты:

\[\large 15000 = c \cdot 2 \cdot 60 \]

Разделим обе части уравнения на число 10:

\[\large 1500 = c \cdot 2 \cdot 6 \]

Теперь разделим обе части уравнения на число 6:

\[\large 250 = c \cdot 2 \]

Разделив обе части на число 2, получим удельную теплоемкость твердого вещества:

Ответ: Удельная теплоемкость твердого вещества \(\large 125 \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \)

Примечание: Тела могут обмениваться тепловой энергией с другими телами. Обмен энергией прекратится при наступлении теплового равновесия. Для решения задач нужно использовать удельные теплоемкости материалов, из которых изготовлены тела. А чтобы рассчитать переданное или полученное телом количество теплоты, нужно уметь применять закон сохранения энергии и составлять уравнение теплового баланса.

Источник

Количество теплоты. Удельная теплоёмкость

1. Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количеством теплоты.

Количеством теплоты называется изменение внутренней энергии тела в процессе теплопередачи без совершения работы.

Количество теплоты обозначают буквой ​ \( Q \) ​. Так как количество теплоты является мерой изменения внутренней энергии, то его единицей является джоуль (1 Дж).

При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.

2. Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество теплоты требуется ему для нагревания. То же самое и с охлаждением: тело большей массы при охлаждении отдаёт большее количество теплоты. Эти тела сделаны из одного и того же вещества и нагреваются они или охлаждаются на одно и то же число градусов.

​3. Если теперь нагревать 100 г воды от 30 до 60 °С, т.е. на 30 °С, а затем до 100 °С, т.е. на 70 °С, то в первом случае на нагревание уйдёт меньше времени, чем во втором, и, соответственно, на нагревание воды на 30 °С, будет затрачено меньшее количество теплоты, чем на нагревание воды на 70 °С. Таким образом, количество теплоты прямо пропорционально разности конечной ​ \( (t_2\,^\circ C) \) ​ и начальной \( (t_1\,^\circ C) \) температур: ​ \( Q\sim(t_2-t_1) \) ​.

4. Если теперь в один сосуд налить 100 г воды, а в другой такой же сосуд налить немного воды и положить в неё такое металлическое тело, чтобы его масса и масса воды составляли 100 г, и нагревать сосуды на одинаковых плитках, то можно заметить, что в сосуде, в котором находится только вода, температура будет ниже, чем в том, в котором находятся вода и металлическое тело. Следовательно, чтобы температура содержимого в обоих сосудах была одинаковой нужно воде передать большее количество теплоты, чем воде и металлическому телу. Таким образом, количество теплоты, необходимое для нагревания тела зависит от рода вещества, из которого это тело сделано.

5. Зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.

Физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К), называется удельной теплоёмкостью вещества.

Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.

Удельная теплоёмкость обозначается буквой ​ \( c \) ​. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг К.

Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.

Удельная теплоёмкость свинца 140 Дж/кг °С. Это значит, что для нагревания 1 кг свинца на 1 °С необходимо затратить количество теплоты 140 Дж. Такое же количество теплоты выделится при остывании 1 кг воды на 1 °С.

Поскольку количество теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.

​По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.

6. Пример решения задачи. В стакан, содержащий 200 г воды при температуре 80 °С, налили 100 г воды при температуре 20 °С. После чего в сосуде установилась температура 60 °С. Какое количество теплоты получила холодная вода и отдала горячая вода?

При решении задачи необходимо выполнять следующую последовательность действий:

1. Условие задачи.

Дано:
​ \( m_1 \) ​ = 200 г
​ \( m_2 \) ​ = 100 г
​ \( t_1 \) ​ = 80 °С
​ \( t_2 \) ​ = 20 °С
​ \( t \) ​ = 60 °С
______________

2. СИ: ​ \( m_1 \) ​ = 0,2 кг; ​ \( m_2 \) ​ = 0,1 кг.

3. Анализ задачи. В задаче описан процесс теплообмена между горячей и холодной водой. Горячая вода отдаёт количество теплоты ​ \( Q_1 \) ​ и охлаждается от температуры ​ \( t_1 \) ​ до температуры ​ \( t \) ​. Холодная вода получает количество теплоты ​ \( Q_2 \) ​ и нагревается от температуры ​ \( t_2 \) ​ до температуры ​ \( t \) ​.

4. Решение задачи в общем виде. Количество теплоты, отданное горячей водой, вычисляется по формуле: ​ \( Q_1=c_1m_1(t_1-t) \) ​.

5. Вычисления.
​ \( Q_1 \) ​ = 4200 Дж/кг · °С · 0,2 кг · 20 °С = 16800 Дж
\( Q_2 \) = 4200 Дж/кг · °С · 0,1 кг · 40 °С = 16800 Дж

6. В ответе получено, что количество теплоты, отданное горячей водой, равно количеству теплоты, полученному холодной водой. При этом рассматривалась идеализированная ситуация и не учитывалось, что некоторое количество теплоты пошло на нагревание стакана, в котором находилась вода, и окружающего воздуха. В действительности же количество теплоты, отданное горячей водой, больше, чем количество теплоты, полученное холодной водой.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Удельная теплоёмкость серебра 250 Дж/(кг · °С). Что это означает?

1) при остывании 1 кг серебра на 250 °С выделяется количество теплоты 1 Дж
2) при остывании 250 кг серебра на 1 °С выделяется количество теплоты 1 Дж
3) при остывании 250 кг серебра на 1 °С поглощается количество теплоты 1 Дж
4) при остывании 1 кг серебра на 1 °С выделяется количество теплоты 250 Дж

2. Удельная теплоёмкость цинка 400 Дж/(кг · °С). Это означает, что

1) при нагревании 1 кг цинка на 400 °С его внутренняя энергия увеличивается на 1 Дж
2) при нагревании 400 кг цинка на 1 °С его внутренняя энергия увеличивается на 1 Дж
3) для нагревания 400 кг цинка на 1 °С его необходимо затратить 1 Дж энергии
4) при нагревании 1 кг цинка на 1 °С его внутренняя энергия увеличивается на 400 Дж

3. При передаче твёрдому телу массой ​ \( m \) ​ количества теплоты ​ \( Q \) ​ температура тела повысилась на ​ \( \Delta t^\circ \) ​. Какое из приведённых ниже выражений определяет удельную теплоёмкость вещества этого тела?

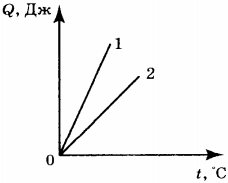
4. На рисунке приведён график зависимости количества теплоты, необходимого для нагревания двух тел (1 и 2) одинаковой массы, от температуры. Сравните значения удельной теплоёмкости (​ \( c_1 \) ​ и ​ \( c_2 \) ​) веществ, из которых сделаны эти тела.

1) ​ \( c_1=c_2 \) ​
2) ​ \( c_1>c_2 \) ​
3) \( c_1
4) ответ зависит от значения массы тел

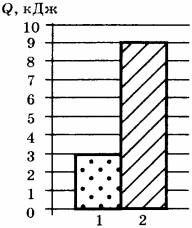
5. На диаграмме представлены значения количества теплоты, переданного двум телам равной массы при изменении их температуры на одно и то же число градусов. Какое соотношение для удельных теплоёмкостей веществ, из которых изготовлены тела, является верным?

1) \( c_1=c_2 \)
2) \( c_1=3c_2 \)
3) \( c_2=3c_1 \)
4) \( c_2=2c_1 \)

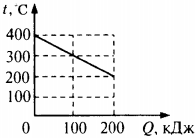
6. На рисунке представлен график зависимости температуры твёрдого тела от отданного им количества теплоты. Масса тела 4 кг. Чему равна удельная теплоёмкость вещества этого тела?

1) 500 Дж/(кг · °С)
2) 250 Дж/(кг · °С)
3) 125 Дж/(кг · °С)
4) 100 Дж/(кг · °С)

7. При нагревании кристаллического вещества массой 100 г измеряли температуру вещества и количество теплоты, сообщённое веществу. Данные измерений представили в виде таблицы. Считая, что потерями энергии можно пренебречь, определите удельную теплоёмкость вещества в твёрдом состоянии.

1) 192 Дж/(кг · °С)
2) 240 Дж/(кг · °С)
3) 576 Дж/(кг · °С)
4) 480 Дж/(кг · °С)

8. Чтобы нагреть 192 г молибдена на 1 К, нужно передать ему количество теплоты 48 Дж. Чему равна удельная теплоёмкость этого вещества?

9. Какое количество теплоты необходимо для нагревания 100 г свинца от 27 до 47 °С?

1) 390 Дж
2) 26 кДж
3) 260 Дж
4) 390 кДж

10. На нагревание кирпича от 20 до 85 °С затрачено такое же количество теплоты, как для нагревания воды такой же массы на 13 °С. Удельная теплоёмкость кирпича равна

1) 840 Дж/(кг · К)
2) 21000 Дж/(кг · К)
3) 2100 Дж/(кг · К)
4) 1680 Дж/(кг · К)

11. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Количество теплоты, которое тело получает при повышении его температуры на некоторое число градусов, равно количеству теплоты, которое это тело отдаёт при понижении его температуры на такое же число градусов.
2) При охлаждении вещества его внутренняя энергия увеличивается.
3) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение кинетической энергии его молекул.
4) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение потенциальной энергии взаимодействия его молекул
5) Внутреннюю энергию тела можно изменить, только сообщив ему некоторое количество теплоты

12. В таблице представлены результаты измерений массы ​ \( m \) ​, изменения температуры ​ \( \Delta t \) ​ и количества теплоты ​ \( Q \) ​, выделяющегося при охлаждении цилиндров, изготовленных из меди или алюминия.

Какие утверждения соответствуют результатам проведённого эксперимента? Из предложенного перечня выберите два правильных. Укажите их номера. На основании проведенных измерений можно утверждать, что количество теплоты, выделяющееся при охлаждении,

1) зависит от вещества, из которого изготовлен цилиндр.
2) не зависит от вещества, из которого изготовлен цилиндр.
3) увеличивается при увеличении массы цилиндра.
4) увеличивается при увеличении разности температур.
5) удельная теплоёмкость алюминия в 4 раза больше, чем удельная теплоёмкость олова.

Часть 2

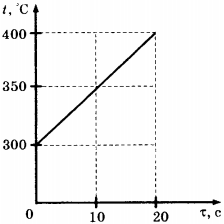
C1.Твёрдое тело массой 2 кг помещают в печь мощностью 2 кВт и начинают нагревать. На рисунке изображена зависимость температуры ​ \( t \) ​ этого тела от времени нагревания ​ \( \tau \) ​. Чему равна удельная теплоёмкость вещества?

1) 400 Дж/(кг · °С)
2) 200 Дж/(кг · °С)
3) 40 Дж/(кг · °С)
4) 20 Дж/(кг · °С)

Источник