какая система координат применяется на геодезических планах
Системы координат в геодезии — какие бывают и как используются?
В данной статье мы разбираем основные вопросы по геодезии. Что такое системы координат, какие виды СК выделяют, какие из них используются на практике и для чего. А также, отвечаем на вопрос, почему мы предоставляем поправки в международной системе координат.
Содержание статьи:
Надеемся, этот материал поможет получить ответы на интересующие вопросы.
Что такое система координат?
Система координат (СК) — это набор математических правил, описывающих, как координаты должны быть соотнесены с точками пространства.
Иными словами, это совокупность условий, определяющих положение и перемещение точки или объекта на прямой, на плоскости, в пространстве с помощью чисел или других символов.
Совокупность чисел, определяющих положение точки, называется координатами этой точки.
Какие бывают системы координат?
Существуют разные геодезические системы координат, они используются в зависимости от масштаба, в котором необходимо произвести расчет расположения объекта на Земле.
В рамках данной статьи, разберемся, какие именно бывают системы координат и как используются на практике в геодезии.
Полярная система координат (полярные координаты)
Полярная система координат — это система координат, положение точки в которой задается расстоянием и направлением от ее начала.
Двумерная полярная система координат может быть задана на плоскости, поверхности сферы или эллипсоида.
Плоская прямоугольная (прямолинейная система координат)
Плоская прямоугольная (прямолинейная) система координат — это система координат, определяющая положение точек по отношению к взаимно перпендикулярным осям, исходящим из ее начала.
Координаты точки в данной системе координат представлены в виде плоских прямоугольных координат x и y. В геодезии — это координаты на плоскости, на которой отображена поверхность земного эллипсоида в заданной картографической проекции.
Прямоугольная пространственная система координат
Прямоугольная пространственная система координат — это система трехмерных линейных прямоугольных координат по координатным осям Х, У, Z координат, у которой оси Х и У лежат в экваториальной плоскости, ось Х направлена к начальному меридиану, ось Z направлена на север, орты образуют правую тройку векторов, а начало координат совпадает с центром земного эллипсоида.
Координаты точки в пространственной системе координат представлены в виде геодезических (эллипсоидальных) координатах или в прямоугольных пространственных координатах.
Земные и референцные системы координат
Помимо вышеупомянутых, различают земные (общеземные) и референцные системы координат. Разбираемся, чем они отличаются.
Что такое земная система координат в геодезии?
Земная система координат — это пространственная система координат, предназначенная для количественного описания положения и движения объектов, находящихся на поверхности Земли и в околоземном пространстве.
Что такое референцная система координат в геодезии?
Референцная система координат — это система координат, созданная с целью обеспечения геодезических и картографических работ на конкретной территории. К ним можно отнести местные и условные системы координат.
Что такое геодезическая система координат?
Геодезическая система координат — это система координат, которая используется для определения точного местоположения объекта на земном шаре.
За земной шар, для удобства проведения математических расчетов в инженерной геодезии, принимают шар с R=6371.11 км. Объем земного шара при этом равен объему земного эллипсоида.
Что такое геодезические координаты?
Геодезические координаты — это величины, два из которых (геодезическая широта B и геодезическая долгота L) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота H) представляет собой высоту точки над поверхностью отсчетного эллипсоида.
В земных системах координат центр координат совпадает с центром масс Земли, поэтому прямоугольные пространственные координаты называют геоцентрическими координатами.
Системы координат также подразделяют на государственные, местные, локальные и международные.
СК, используемые на практике
Практическими реализациями пространственной геоцентрической земной системы координат являются системы координат WGS-84, ПЗ-90.11 и ГСК-2011.
Система координат WGS-84
WGS-84 (World Geodetic System (Всемирная геодезическая система координат)) – это система геодезических параметров Земли 1984 года, используемая в GPS, в число которых входит система геоцентрических координат).
Система координат ПЗ-90.11
ПЗ-90.11 (общеземная геоцентрическая система координат «Параметры Земли 1990 года») — это государственная система координат, используемая в ГЛОНАСС.
ПЗ-90.11 была установлена постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования в целях геодезического обеспечения орбитальных полетов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны Российской Федерации.
Система координат ГСК-2011
ГСК-2011 (геодезическая система координат 2011 года) – это государственная система координат, установленная постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования при осуществлении геодезических и картографических работ на территории Российской Федерации.
Система координат МСК
МСК – это местная система координат субъекта Российской Федерации, установленная для целей обеспечения проведения геодезических и картографических работ при осуществлении градостроительной и кадастровой деятельности, землеустройства, недропользования и иной деятельности.
Каждый субъект имеет свою МСК с номером данного субъекта, например, местная система координат Московской области именуется МСК-50.
Архивные системы координат
Существуют архивные системы координат, которые в настоящее время не используются (не действуют).
Среди них можно выделить:
Какие бывают системы отсчета высот?
Высоты в геодезии могут быть представлены в виде геодезических, ортометрических и нормальных и высот. Высоты также могут быть представлены в условной системе высот.
Основные системы отсчета высот:
Отсчет высот в Балтийской системе высот 1977 года ведется от нуля Кронштадтского футштока, укрепленного в устое моста через обводной канал в г. Кронштадте.
Почему мы предоставляем поправки в международной системе координат?
Поскольку ГНСС работают в реализациях земной геоцентрической системы координат, таких как WGS-84 и ПЗ-90.11, то первоначально все спутниковые определения с использованием ГНСС выполняются в этих системах координат.
В ГНСС аппаратуре и программном обеспечении все результаты (координаты, скорости, ускорения) вначале приводятся в WGS-84, которые можно представить в любой другой системе координат путем математических преобразований.
Координаты в пространственных земных системах WGS-84, ПЗ-90.11 или ГСК-2011 с точностью 1 метр практически совпадают, поэтому для спутниковых определений с такой точностью не имеет значения в какой из реализаций системы координат они представлены.
Для спутниковых определений с высокой точностью мы предоставляем дифференциальные поправки, которые применяются к измеряемым величинам в процессе спутниковых определений. Дифференциальные поправки позволяют определить пространственные координаты относительно спутниковых базовых станций с заданными координатами.
Поскольку в нашей сети координаты всех станций определены в международной системе координат WGS-84, координаты определяемых вами точек также первоначально представлены в WGS-84. Но, как уже было сказано выше, они могут быть преобразованы в любую системы координат по известным параметрам преобразования.
Системы координат, применяемые в геодезии
С помощью координат можно точно определить положение объекта. Однако известно, что наша планета имеет сложную форму.
Поэтому системы координат (СК), применяемые в геодезии, могут иметь несколько видов. Они применяются для того, чтобы точно определить расположение объекта.
Геодезическая система координат
Данные, которые должны быть привязаны к определённому месту на земной поверхности, играют важную роль в различных сферах человеческой деятельности.
Вот несколько примеров:
при создании карт во время проведения топографической съёмки для отображения расположения предметов и их высот;
для решения различных задач в навигации;
при использовании спутниковых навигационных систем.
СК строится следующим образом:
Проводится плоскость через экватор (экваториальная).
Перпендикулярно ей рассматривается такая, которая проходит через нулевой меридиан.
Фиксируется расположение центра земли и полюсов.
Чтобы определить положение точки на Земле, к ней проводят отрезок, который перпендикулярен этому участку Земли. Обычно он отличается от того, который соединяется с центром планеты.
Строится сечение, проходящее через нормаль и полюса. Определяется угол, который она образует с проходящим через начальный геодезический меридиан. Таким образом определяется геодезический меридиан объекта.
Определяется ещё одно сечение, содержащее нормаль и оба полюса планеты. Здесь определяется линия пересечения с экваториальной. Теперь осталось определить угол между этой линией и нормалью, который равняется параллели этого места.
Астрономическая система координат
Земля имеет форму, которая называется геоидом. При использовании астрономических показателей требуется определить положение объекта на её поверхности с помощью определения астрономической широты и долготы.
Для вычисления первой из этих величин необходимо мысленно провести перпендикуляр к поверхности Земли в месте, для которого определяется положение.
Для определения широты определяется угол с экваториальной плоскостью.
Для вычисления долготы требуется вычислить двугранный угол плоскости, включающей в себя астрономическую нормаль и полюса, и той, которая включает в себя гринвичский меридиан.
Для вычисления чисел в этой СК пользуются специальными инструментами для точных астрономических измерений углов и их приращений. Важно отметить, что нормаль в этой СК не совпадает с той, которая используется в геодезической. Если совпадения бывают, то они очень редки.
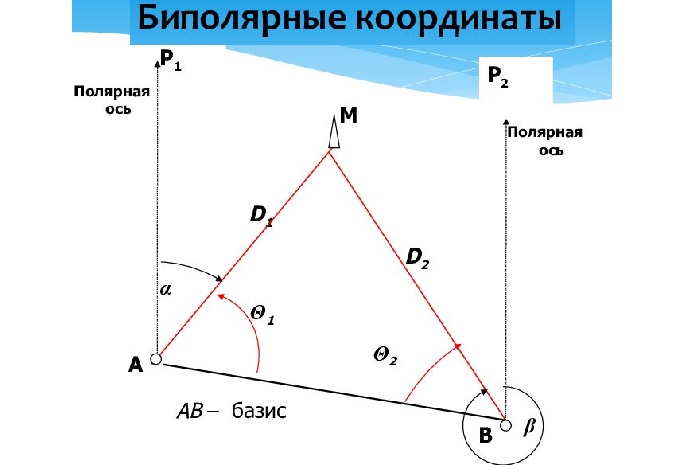
Полярная и биполярная система координат
В этом случае основой для определения положения места является использование полярной оси и её начала. В этом случае допускается применение линий, выбранных каким-либо удобным способом.
При определении местоположения нужно зафиксировать угол с полярной осью и расстояние от точки отсчёта. Такую СК применяют при работе на местности.
При работе с биполярной СК на местности используются две полярных оси.
Направление на искомую точку будет иметь определённый угол с одной и с другой. Будет зафиксировано два расстояния: от одной начальной точки и от другой.
Сферическая система координат
Форма Земли более сложная по сравнению с правильной сферой. Однако при составлении карт, которые охватывают сравнительно небольшую площадь, для простоты предполагают, что планета представляет собой правильный шар.
В этом случае определение показателей происходит аналогично тому, как это делается в геодезической СК, но здесь вместо нормали используется отрезок между геометрическим центром сферы и точкой на поверхности.
Здесь используются сферическая широта и долгота.
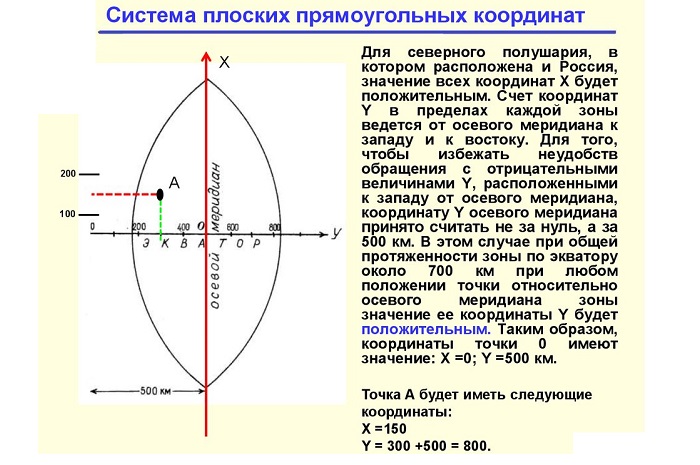
Система плоских прямоугольных координат
Для определения положения тел на земной поверхности можно использовать обычную прямоугольную СК.
Чтобы построить её центр и оси, необходимо учесть следующее:
В качестве исходной точки рассматривается центр масс нашей планеты.
Ось Z совпадает с осью вращения.
Ось X проходит через пересечение экваториальной плоскости, той, которая проходит через полюса и гринвичский географический меридиан и поверхности земного шара.
Y также проходит через экваториальную плоскость и поверхность планеты. Она перпендикулярна осям X и Z. Эта ось смотрит так, чтобы поворот от X к Y, если смотреть от Z, выполнялся бы против часовой стрелки.
Плоскую прямоугольную СК можно применять для местной топографической съёмки. В этом случае фиксируют перпендикулярные оси и устанавливают показатели, соответствующие расположению данной точки.
Cистемы координат, применяемые в топографии и геодезии
Cистемы координат, применяемые в топографии и геодезии
Координаты – это величины, определяющие положение любой точки на поверхности или в пространстве в принятой системе координат. Система координат устанавливает начальные (исходные) точки, линии или плоскости для отсчета необходимых величин – начало отсчета координат и единицы их исчисления. В топографии и геодезии наиболь¬шее применение получили системы географических, прямоугольных, полярных и биполярных координат.
Параллелью называют линию сечения эллипсоида плоскостью, проходящей через данную точку и пер¬пендикулярную земной оси. Параллель, плоскость которой проходит через центр эллипсоида, называется экватором. Через каждую точку, лежащую на поверхности земного шара, можно провести только один меридиан и только одну параллель.
Географические координаты – это угловые величины: долгота l и широта j.
Географической долготой l называется двугранный угол, заключенный между плоскостью данного меридиана (проходящего через точку В) и плоскостью начального меридиана. За начальный (нулевой) меридиан принят меридиан, проходящий через центр главного зала Гринвичской обсерватории в пределах г. Лондона. Для точки В долгота определяется углом l = WCD. Счет долгот ведут от начального меридиана в обе стороны – на восток и на запад. В связи с этим различают западные и восточные долготы, которые изменяются от 0° до 180°.
Географической широтой j называется угол, составленный плоскостью экватора и отвесной линией, проходящей через данную точку. Если Землю принимать за шар, то для точки В (рис. 2.8) широта j определяется углом DCB. Широты, отсчитываемые от экватора к северу, называются северными, а к югу – южными, они изменяются от 0° на экваторе до 90° на полюсах.
Географические координаты могут быть получены на основании астрономических наблюдений или геодезических измерений. В первом случае их называют астрономическими, а во втором – геодезическими (L – долгота, B – широта). При астрономических наблюдениях проецирование точек на поверхность относимости осуществляется отвесными линиями, при геодезических измерениях – нормалями. Поэтому величины астрономических и геодезических координат отличаются на величину уклонения отвесной линии.
Использование разными государствами различных референц-эллипсоидов приводит к различиям координат одних и тех же пунктов, вычисленных относительно разных исходных поверхностей. Практически это выражается в общем смещении картографического изображения относительно меридианов и параллелей на картах крупного и среднего масштабов.
Прямоугольными координатами называются линейные величины – абсцисса и ордината, определяющие положение точки на плоскости относительно исходных направлений.
(рис. 2.9)
В геодезии и топографии принята правая система прямоугольных координат. Это отличает ее от левой системы координат, используемой в математике. Исходными направлениями служат две взаимно перпендикулярные линии с началом отсчета в точке их пересечения О.
Прямая ХХ (ось абсцисс) совмещается с направлением меридиана, проходящего через начало координат, или с направлением, параллельным некоторому меридиану. Прямая YY (ось ординат) проходит через точку О перпендикулярную оси абсцисс. В такой системе положение точки на плоскости определяется кратчайшим расстоянием до нее от осей координат. Положение точки А определяется длиной перпендикуляров Xа и Yа. Отрезок Xа называется абсциссой точки А, а Yа – ординатой этой точки. Прямоугольные координаты обычно выражаются в метрах. Осями абсцисс и ординат участок местности в точке О делится на четыре четверти (рис. 2.9). Название четвертей определяется принятыми обозначениями стран света. Четверти нумеруются по направлению хода часовой стрелки: I – СВ; II – ЮВ; III – ЮЗ; IV – СЗ.
В табл. 2.3 показаны знаки абсцисс Х и ординат Y для точек, находящихся в разных четвертях и даны их названия.
Таблица 2.3
Абсциссы точек, расположенные вверх от начала координат считаются положительными, а вниз от нее – отрицательными, ординаты точек, расположенные вправо – положительными, влево – отрицательными. Система плоских прямоугольных координат применяется на ограниченных участках земной поверхности, которые могут быть приняты за плоские.
Координаты, началом отсчета которых является какая-либо точка местности, называются полярными. В данной системе координат производится измерение углов ориентирования. На горизонтальной плоскости (рис. 2.10) через произвольно выбранную точку О, называемую полюсом, проводят прямую ОХ – полярную ось.
Рис. 2.12
Высоты точек земной поверхности. Для определения положения точек физической поверхности Земли недостаточно знать только плановые координаты X, Y или l, j, необходима третья координата – высота точки Н. Высотой точки Н (рис. 2.12) называется расстояние по отвесному направлению от данной точки (А´; В´´) до принятой основной уровенной поверхности MN. Числовое значение высоты точки называется отметкой. Высоты, отсчитываемые от основной уровенной поверхности MN, называют абсолютными высотами (АА´; ВВ´´), а определяемые относительно произвольно выбранной уровенной поверхности – условными высотами (В´В´´). Разность высот двух точек или расстояние по отвесному направлению между уровенными поверхностями, проходящими через две любые точки Земли называется относительной высотой (В´В´´) или превышением этих точек h.
В Республике Беларусь принята Балтийская система высот 1977 г. Счет высот ведется от уровенной поверхности, совпадающей со средним уровнем воды в Финском заливе, от нуля Кронштадского футштока.
Какая система координат применяется на геодезических планах
Статья 7. Системы координат, государственная система высот и государственная гравиметрическая система
1. Геодезические и картографические работы выполняются с использованием государственных, местных, локальных и международных систем координат, государственной системы высот и государственной гравиметрической системы.
2. Государственные системы координат, государственная система высот и государственная гравиметрическая система устанавливаются Правительством Российской Федерации.
3. Порядок установления местных систем координат определяется федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно-правовому регулированию в сфере геодезии и картографии.
4. Локальные системы координат могут устанавливаться и использоваться заинтересованными лицами самостоятельно, в том числе для выполнения геодезических и картографических работ при осуществлении градостроительной деятельности.
5. К международным системам координат относятся системы координат, использование которых предусмотрено международными договорами Российской Федерации, и системы координат зарубежных спутниковых навигационных систем.
6. Определение параметров фигуры и гравитационного поля Земли, иных параметров, необходимых для установления государственной системы координат, используемой при выполнении геодезических и картографических работ на территории Российской Федерации, государственной системы высот, государственной гравиметрической системы, и параметров перехода между указанной государственной системой координат и местными и международными системами координат осуществляется федеральным государственным учреждением, подведомственным федеральному органу исполнительной власти, уполномоченному на оказание государственных услуг в сфере геодезии и картографии.
7. Определение параметров фигуры и гравитационного поля Земли, необходимых для установления государственной системы координат, используемой в целях геодезического обеспечения орбитальных полетов, решения задач в сфере навигационной деятельности и задач в области обороны Российской Федерации, и параметров перехода между указанной государственной системой координат и международными системами координат осуществляется федеральным государственным учреждением, подведомственным федеральному органу исполнительной власти, осуществляющему функции по выработке и реализации государственной политики, нормативно-правовому регулированию в области обороны.
Геодезическая основа кадастра. Использование геодезического метода и метода спутниковых геодезических измерений
Автор: Дехканова Н.Н., к.э.н., начальник отдела геодезии и картографии Управления Федеральной службы государственной регистрации, кадастра и картографии по Кировской области.
Сегодня мы будем говорить о геодезической основе кадастра и рассмотрим два из пяти методов, использование которых законодательно установлено при определении координат характерных точек границ земельного участка, а также контура здания, сооружения или объекта незавершённого строительства на земельном участке. Это геодезический метод и метод спутниковых геодезических измерений (определений). Разговор коснётся заполнения реквизитов:
Законодательную основу сегодняшней темы составляют положения 15 документов:
Геодезический метод и метод спутниковых геодезических измерений при определении координат точек – это два метода, которые требуют наличия определённых знаний, связанных с непосредственными измерениями на местности с использованием соответствующих средств измерения.
Хочется вернуться к выступлению от 03.02.2016, где мной было подчёркнуто следующее:
«Особенно важно понять, что при оформления межевых/технических планов кадастровые инженеры должны хотя бы в общем представлять технологию производства геодезических измерений на конкретном объекте, если они не являются непосредственными исполнителями геодезических работ. В противном случае факт внесения некачественных, а порой и недостоверных или даже противоречивых сведений неизбежен. Следовательно, для внесения необходимых сведений исполнитель геодезических измерений обязан представить кадастровому инженеру такой пакет документов, который будет достаточным для внесения обязательной информации в межевой/технический план.
Обратимся к статье 6 Закона о кадастре.
В соответствии с частью 1 статьи 6 геодезической основой кадастра являются государственная геодезическая сеть и опорные межевые сети.
В соответствии с частью 3 статьи 6 сведения о геодезической основе кадастра вносятся в кадастр на основании подготовленных в результате выполнения указанных работ документов.
Требования по внесению сведений о геодезической основе кадастра установлены:
При выполнении геодезических работ для целей постановки на учёт земельных участков, зданий, сооружений, объектов незавершённого строительства геодезические измерения осуществляются на основе одних и тех же требований действующего законодательства, поэтому снова рассмотрим применение соответствующих требований законодательства на примере оформления межевого плана, как наиболее сложного.
Пункт 34 Приказа №412 устанавливает обязанность внесения в реквизите «2» раздела «Исходные данные»:
Государственная геодезическая сеть, опорная межевая сеть. В чём их отличие? Что они собой представляют? Для кого-то ответы на эти вопросы не вызывают затруднений, однако не для всех кадастровых инженеров, да и порой самих исполнителей геодезических работ.
Опорным пунктом называется закреплённая на местности точка, координаты которой известны из геодезических измерений с достаточной точностью.
Совокупность опорных пунктов, равномерно расположенных по всей территории и служащих основой для съёмок, называется опорной сетью.
Геодезическая сеть, используемая для обеспечения топосъёмок, называется съёмочным обоснованием. Это съёмочные сети и сети более высокого порядка, расположенные на участке съёмки.
Геодезическая опорная сеть представляет собой совокупность закреплённых на земной поверхности пунктов, положение которых определено в единой системе координат. Положение опорных пунктов на местности может определяться астрономическим, геодезическим, спутниковым (космическим) и другими способами.
Согласно принципу перехода «от общего к частному» вся опорная сеть подразделяется на классы, и построение её осуществляется несколькими ступенями: от сетей более высокого класса к сетям низшего, от крупных и точных геометрических построений к более мелким и менее точным. Пункты высших классов располагаются на больших (до нескольких десятков километров) расстояниях друг от друга и затем последовательно сгущаются путём развития между ними сетей более низких классов.
Геодезические сети принято подразделять на следующие виды:
Густота геодезических сетей и необходимая точность нахождения планового положения пункта определяются характером инженерно-технических задач, решаемых на этой основе.
Различают плановые геодезические сети, в которых для каждого пункта определяют прямоугольные координаты (х и у) в общегосударственной системе, и высотные, в которых высоты пунктов определяют в Балтийской системе высот.
Что же такое Государственная геодезическая сеть (далее сокращённо будем называть ГГС)? Чем она отличается от опорной межевой сети (далее – сокращённо ОМС)?
ГГС страны является главной геодезической основой топографических съёмок всех масштабов.
В соответствии с пунктом 2.2.1 «Основных положений о государственной геодезической сети» (далее – Основные положения о ГГС): ГГС, созданная по состоянию на 1995 год, объединяет в одно целое:
Пункты ГГС имеют между собой надёжные геодезические связи.
В соответствии с пунктом 3.1.3. Основных положений о ГГС:
Государственная геодезическая сеть структурно формируется по принципу перехода от общего к частному и включает в себя геодезические построения различных классов точности:
В указанную систему построений вписываются также существующие сети триангуляции и полигонометрии 1. 4 классов.
На основе новых высокоточных пунктов спутниковой сети создаются постоянно действующие дифференциальные станции с целью обеспечения возможностей определения координат потребителями в режиме, близком к реальному времени.
Важно! Пунктом 3.1.4. Основных положений о ГГС предусмотрено:
По мере развития сетей ФАГС, ВГС и СГС-1 выполняется уравнивание ГГС и уточняются параметры взаимного ориентирования геоцентрической системы координат и системы геодезических координат СК-95.
На сегодняшний день для нас с вами представляют наибольший интерес астрономо-геодезическая сеть и геодезические сети сгущения.
В соответствии с Основными положениями о ГГС:
2.2.4. Астрономо-геодезическая сеть состоит из 164306 пунктов и включает в себя ряды триангуляции 1 класса, сети триангуляции и полигонометрии 1 и 2 классов.
2.2.4.1. Астрономо-геодезическая сеть 1 и 2 классов содержит 3,6 тысячи геодезических азимутов, определенных из астрономических наблюдений, и 2,8 тысячи базисных сторон, расположенных через 170. 200 км.
2.2.5. Геодезические сети сгущения 3 и 4 классов включают в себя около 300 тысяч пунктов. Эти сети созданы методами триангуляции, полигонометрии и трилатерации
2.2.6. Плотность пунктов ГГС 1, 2, 3 и 4 классов, как правило, составляет не менее одного пункта на 50 кв. км.
2.2.7. На пунктах геодезических сетей 1, 2, 3 и 4 классов определены по два ориентирных пункта с подземными центрами.
Плановые геодезические сети создают методами триангуляции, трилатерации, полигонометрии и их сочетаниями.
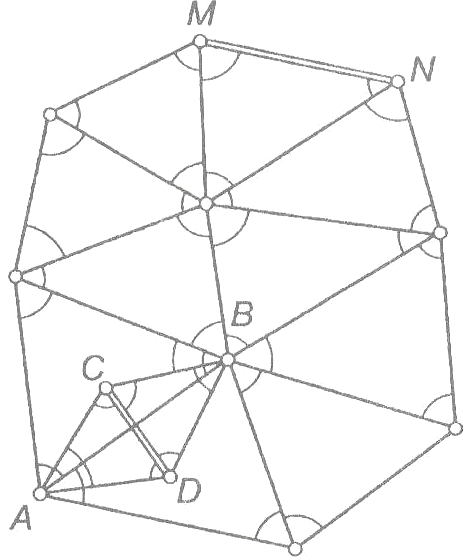
Триангуляция заключается в построении на местности систем треугольников, в которых измеряются все углы и длины некоторых базисных сторон (рис. 1). Длины других сторон рассчитываются по известным формулам тригонометрии.
Рисунок 1. Триангуляция
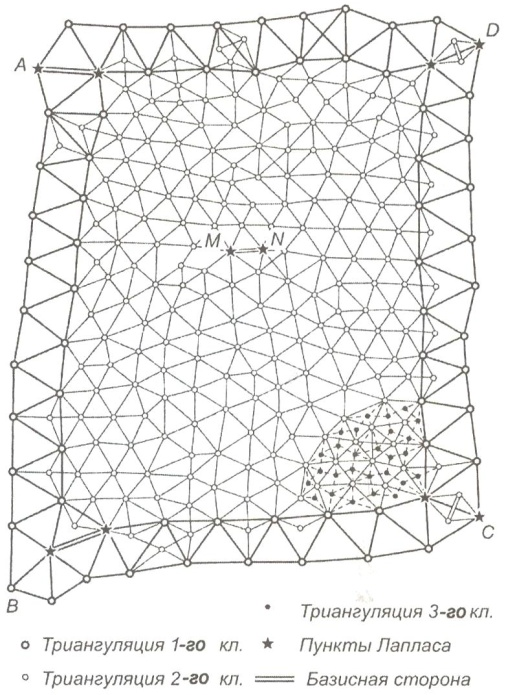
Триангуляция 1-го класса создаётся в виде астрономо-геодезической сети и призвана обеспечить решение основных научных задач, связанных с определением формы и размеров Земли. Она является главной основой развития сетей последующих классов и служит для распространения единой системы координат на всю территорию страны. Её построение осуществляют с наивысшей точностью, которую могут обеспечить современные приборы при тщательно продуманной методике измерений.
Сети триангуляции 1-го класса представляют собой ряды треугольников, близких к равносторонним, располагаемых вдоль меридианов и параллелей и отстоящих друг от друга на 200км. Пересекаясь между собой, ряды треугольников образуют замкнутые полигоны периметром 800 – 1000км (рис. 1).
Триангуляция 2-го класса – сплошные сети треугольников, заполняющих полигоны триангуляции 1-го класса. Она является опорной сетью, служащей для развития сетей последующего сгущения и геодезического обоснования всех топографических съёмок.
Триангуляция 3-го и 4-го классов является дальнейшим сгущением ГГС, служит для обоснования топографических съёмок крупного масштаба и представляет собой вставки жёстких систем или отдельных пунктов в сети старших классов.
Основные характеристики триангуляционной сети 1 – 4 классов
Допустимая средняя квадратическая погрешность измерения углов