какая система называется дискретной в цифровой обработке сигналов
Аналоговые, дискретные и цифровые сигналы
Любая физическая величина по характеру изменения ее значения может быть постоянной (если она имеет только одно фиксированное значение), дискретной (если она может иметь два или более фиксированных значений), или аналоговой (если она может иметь бесчисленное множество значений). Все эти величины могут быть преобразованы в цифровую форму.
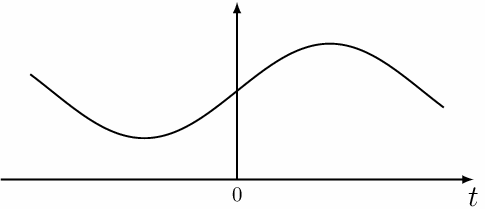
Аналоговым называется такой сигнал, который может быть представлен непрерывной линией из множества значений, определенных в каждый момент времени относительно временной оси. Значения аналогового сигнала произвольны в каждый момент времени, поэтому он может быть в принципе представлен как некая непрерывная функция (зависящая от времени как от переменной) либо как кусочно-непрерывная функция времени.
Аналоговым сигналом можно назвать, например, звуковой сигнал, генерируемый обмоткой электромагнитного микрофона или ламповым акустическим усилителем, поскольку такой сигнал непрерывен и его значения (напряжение или ток) сильно отличаются друг от друга в каждый момент времени.
На приведенном ниже рисунке изображен пример подобного рода аналогового сигнала.
Аналоговые величины могу иметь бесконечное множество значений в определенных пределах. Они непрерывны и их значения не могут изменяться скачками.
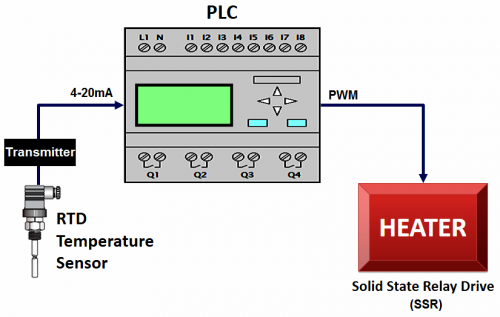
Пример аналогового сигнала: термопара передает в аналоговом виде значение температуры в программируемый логический контроллер, который управляет с помощью твердотельного реле температурой в электрической печи.
Если некий сигнал принимает произвольные значения лишь в отдельные моменты времени, то такой сигнал называют дискретным. Чаще всего на практике применяются дискретные сигналы, распределенные по равномерной временной решетке, шаг которой называется интервалом дискретизации.
Дискретный сигнал принимает определенные не нулевые значения лишь в моменты дискретизации, то есть он является не непрерывным в отличие от аналогового сигнала. Если из звукового сигнала вырезать небольшие кусочки определенного размера через равные интервалы, такой сигнал можно будет назвать дискретным.
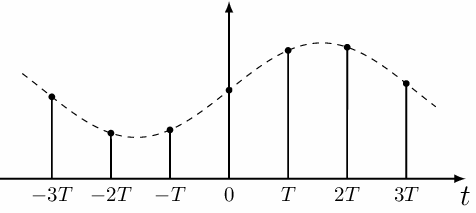
Ниже приведен пример формирования подобного дискретного сигнала с интервалом дискретизации Т. Обратите внимание, что квантуется лишь интервал дискретизации, но не сами значения сигнала.
Дискретные сигналы имеют два и более фиксированных значений (количество их значений всегда выражается целыми числами).
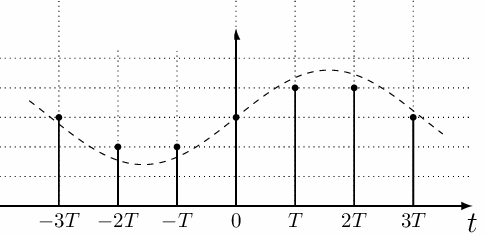
Когда дискретный сигнал принимает только какие-то фиксированные значения (которые могут быть расположены по сетке с определенным шагом), такие что они могут быть представлены как количество квантовых величин, такой дискретный сигнал называется цифровым. То есть цифровой сигнал — это такой дискретный сигнал, который квантован не только по промежуткам времени, но и по уровню.
Практически дискретные и цифровые сигналы в ряде задач отождествляются, и могут быть легко заданы в форме отсчетов с помощью вычислительного устройства.
На рисунке приведен пример формирования цифрового сигнала на базе аналогового. Обратите внимание, что значения цифрового сигнала не могут принимать промежуточных значений, а только определенные — целое количество вертикальных шагов сетки.
Цифровой сигнал легко записывается и перезаписывается в память вычислительных устройств, просто считывается и копируется без потери точности, тогда как перезапись аналогового сигнала всегда сопряжена с утратой некоторой, пусть и незначительной, части информации.
Обработка цифровых сигналов позволяет получать устройства с очень высокими характеристиками благодаря выполнению вычислительных операций совершенно без потерь качества, либо с пренебрежимо малыми потерями.
В силу этих достоинств, именно цифровые сигналы повсеместно распространены сегодня в системах хранения и обработки данных. Вся современная память — цифровая. Аналоговые носители информации (такие как пленочные кассеты и т.д.) давно ушли в прошлое.
Аналоговый и цифровой приборы для измерения напряжения:
Но даже у цифровых сигналов есть свои недостатки. Их невозможно передать напрямую как есть, ибо передача обычно реализуется посредством непрерывных электромагнитных волн. Поэтому при передаче и приеме цифровых сигналов необходимо прибегать к дополнительной модуляции и аналого-цифровому преобразованию. Меньший динамический диапазон цифровых сигналов (отношение наибольшего значения к наименьшему), обусловленный квантованностью значений по сетке, является еще одним их недостатком.
Существуют и такие области, где аналоговые сигналы незаменимы. Например аналоговый звук никогда не сравнится с цифровым, поэтому ламповые усилители и пластинки до сих пор не выходят из моды, несмотря на обилие цифровых форматов записи звука с самой высокой частотой дискретизации.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Аналоговые, дискретные и цифровые сигналы
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Указанные преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.
Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).
Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.
Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).
Оценка дискретного сигнала может быть представлена в виде
При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:
Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:
Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:
Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :
В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.
Какая система называется дискретной в цифровой обработке сигналов
Двумя самыми фундаментальными понятиями в данном курсе являются понятия сигнала и системы.
Под сигналом понимается физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.
Одномерные сигналы описываются вещественной или комплексной функцией 

Энергией сигнала x ( t ) называется величина

Если 

Если сигнал имеет ограниченную энергию, то он ограничен.
Мощностью сигнала x ( t ) называется величина

Если 
В реальной природе сигналов с неограниченной энергией и мощностью не существует. Большинство сигналов, существующих в реальной природе являются аналоговыми.
Аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией 




Важным примером аналогового сигнала является сигнал, описываемый т.н. «единичной функцией», которая описывается выражением

где 
График единичной функции представлен на рис.1.2.
 |

 |
В этом случае функцию 1( t ) можно записать как


 |


 |
1. 
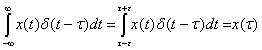





график которой представлен на рис.1.6.
 |
 |

Процесс восстановления аналогового сигнала из дискретного называется временная экстраполяция.
Для дискретных последовательностей также вводятся понятия энергии и мощности. Энергией последовательности x ( n ) называется величина

Мощностью последовательности x ( n ) называется величина

Для дискретных последовательностей сохраняются те же закономерности, касающиеся ограничения мощности и энергии, что и для непрерывных сигналов.
Периодической называют последовательность x ( nT ), удовлетворяющую условию x ( nT )= x ( nT + mNT ), где m и N – целые числа. При этом N называют периодом последовательности. Периодическую последовательность достаточно задать на интервале периода, например при 
Цифровые сигналы представляют собой дискретные сигналы, которые в дискретные моменты времени могут принимать лишь конечный ряд дискретных значений – уровней квантования. Процесс преобразования дискретного сигнала в цифровой называется квантованием по уровню. Цифровые сигналы описываются квантованными решетчатыми функциями x ц ( nT ). Примеры цифровых сигналов представлены на рис. 1.8а и 1.8б.

Т.о., квантование дискретных сигналов состоит в представлении отсчета сигнала x д ( nT ) с помощью двоичного числа, содержащего m разрядов. В результате квантования отсчет представляется с ошибкой, которая называется ошибкой квантования

Шаг квантования Q определяется весом младшего двоичного разряда результирующего числа

Основными способами квантования являются усечение и округление.

График функции усечения дополнительного кода представлен на рис.1.9, а прямого кода – на рис.1.10.
 | |
 |

График функции округления представлен на рис. 1.11.
Рассмотрение и использование различных сигналов предполагает возможность измерения значения этих сигналов в заданные моменты времени. Естественно возникает вопрос о достоверности (или наоборот, неопределенности) измерения значения сигналов. Этими вопросами занимается теория информации, основоположником которой является К.Шеннон. Основная идея теории информации состоит в том, что с информацией можно обращаться почти также, как с такими физическими величинами как масса и энергия.
Если предположить, что все результаты измерения в пределах от x 1 до x 2 равновероятны, т.е. плотность распределения вероятности для различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности p ( x ).
Поскольку полная вероятность получить отсчет где-то в пределах от x 1 до x 2 равна 1, то под кривой должна быть заключена площадь, равная 1, а это значит, что


Получение каой-либо информации об интересующей нас величине заключается, таким образом, в уменьшении неопределенности ее значения.

В большинстве случаев неопределенность знания о значении сигнала определяется действием помех или шумов. Дезинформационное действие шума при передаче сигнала определяется энтропией шума как случайной величины. Если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписывать определенную величину энтропии, которая и характеризует его дезинформационное действие. При этом анализ системы можно проводить раздельно для шума и сигнала, что резко упрощает решение этой задачи.

Если кроме основного канала передачи сигнала имеется дополнительный канал, то для исправления ошибок, возникших от шума с энтропией H ( D ), по этому каналу необходтмо передать дополнительное количество информации, не меньшее чем

Эти данные можно так закодировать, что будет возможно скорректировать все ошибки, вызванные шумом, за исключением произвольно малой доли этих ошибок.
В нашем случае, для равномерно распределенной случайной величины, энтропия определяется как

а оставшаяся или условная энтропия результата измерения после получения отсчета xn равна

Отсюда полученное количество информации равное разности исходной и оставшейся энтропии равно

При анализе систем с цифровыми сигналами ошибки квантования рассматриваются как стационарный случайный процесс с равномерным распределением вероятности по диапазону распределения ошибки квантования. На рис. 1.12а, б и в приведены плотности вероятности ошибки квантования при округлении дополнительного кода, прямого кода и усечении соответственно.
Какая система называется дискретной в цифровой обработке сигналов
Рассмотрим системы автоматического управления, в которых передача, обработка и преобразование информации осуществляются только в определенные моменты времени, то есть дискретно. В этом случае в системах действуют сигналы, являющиеся некоторой последовательностью импульсов, и такие системы называются дискретными. Создание дискретных систем может быть вызвано многими причинами.
Во-первых, принцип действия некоторых элементов, входящих в систему, может быть дискретным. К примеру, в системе управления ракетой имеется импульсная радиолокационная станция (РЛС), измеряющая координаты цели и ракеты (рис. 1.1). По своему принципу действия она выдает информацию дискретно с частотой следования импульсов станции, поэтому и вся система управления будет дискретной. В качестве другого примера можно указать на САУ, имеющие в своем составе цифровые вычислительные машины (ЦВМ), являющиеся дискретными устройствами.
Во-вторых, в дискретных системах проще реализовать сложные алгоритмы управления. Так, при использовании ЦВМ алгоритм задается в виде программы, сложность которой практически не влияет на конструкцию системы. Смена программы, то есть алгоритма управления, производится без больших затрат времени. В непрерывных же САУ повышение сложности алгоритма управления требует включения в состав системы новых элементов, а замена алгоритма связана с существенным усложнением конструкции.
Перечисленные преимущества привели к широкому использованию дискретных систем. Особенно большое распространение получили системы с ЦВМ. Классификация дискретных систем базируется на признаках, определяющих особенности протекания процессов управления и методики исследования. По этим признакам дискретные системы можно разделить на линейные и нелинейные (в зависимости от применимости к ним принципа суперпозиции) и на стационарные и нестационарные (по степени изменения параметров во времени). Кроме них имеются и другие признаки, характерные только для дискретных систем. Перечислим их и дадим дополнительную классификацию дискретных САУ.
Рис. 1.2. Квантование сигналов по времени (а); уровню (б); по времени и по уровню (в)
Если каждый квант информации дискретного процесса, квантованного только по времени, передается с помощью импульса при определенном виде модуляции его параметров, то дискретные системы называются импульсными. В итоге различают импульсные системы с амплитудной (АИМ), широтной (ШИМ), фазовой (ФИМ), частотной (ЧИМ) видами модуляции. Кроме того, бывают системы с комбинированными видами модуляции. Если в системах с АИМ амплитуда импульсов пропорциональна значениям квантованного процесса, то такие импульсные системы могут быть линейными. При всех других видах модуляции они относятся к классу нелинейных систем.
Если в дискретных САУ преобразуются процессы, квантованные по уровню, то они называются релейными. Системы с квантованием процессов по времени и уровню называются цифровыми. Как релейные, так и цифровые системы являются нелинейными. Если все сигналы в системе являются дискретными, то она называется чисто дискретной, если же часть сигналов остается непрерывными, то дискретно-непрерывной. Так как в чисто дискретной системе все сигналы и, следовательно, процессы имеют одинаковую дискретную структуру, то теория таких систем сравнительно проще. Дискретно-непрерывные системы являются промежуточным случаем между непрерывными и чисто дискретными, поэтому методика их исследования сложнее, так как она должна включать в себя элементы теории как непрерывных, так и чисто дискретных систем. Исходя из этого, целесообразно теорию дискретных систем начинать с изучения систем чисто дискретных, распространив затем полученные результаты на дискретно-непрерывные. Чтобы не усложнять терминологию, чисто дискретные системы в дальнейшем будем называть просто дискретными. Там, где это необходимо по ходу описания, будет применяться полный термин “чисто дискретная система”. В развитие теории дискретных систем большой вклад внесли советские ученые Я. 3. Ципкин [16], Л. Т. Кузин [10] и целый ряд других.
В процессе изложения дальнейшего материала мы не будем касаться вопросов теории релейных систем, а также импульсных систем с ШИМ, ФИМ и ЧИМ. Основные сведения по этим системам можно найти в указанной выше литературе. Таким образом, мы сосредоточим наше внимание на цифровых системах и импульсных с амплитудно-импульсной модуляцией. С точки зрения видов квантования, показанных на рис. 1.2, будем рассматривать только процессы с квантованием по времени и по времени и уровню одновременно (рис. 1.2, а и б).
1.2. Особенности процессов в дискретных системах
В дискретных системах осуществляется преобразование информации, заданной в виде дискретных процессов, квантованных по времени или по времени и уровню одновременно. Введем специальные обозначения для этих процессов. Исходные непрерывные процессы, из которых получаются дискретные, называются огибающими и обозначаются обычными символами, например x(t).
Соответствующие им дискретные процессы с квантованием по времени (рис. 1.2, а) и постоянным периодом Tn, обозначают через x(iTn), имея в виду, что i может быть любым целым числом. Чтобы получить дискретный процесс, квантованный по времени, по заданной огибающей достаточно в функции x(t) положить значение t = iTn, то есть
Дискретный процесс, квантованный по времени с постоянным периодом Tn и по уровню с постоянным шагом Δ, будем обозначать символом х(iTn) (рис. 1.2, б). Получить его по заданной функции огибающей можно по формуле
где F обозначает операцию нахождения ближайшего к значению х(iТn) числа с шагом квантования по уровню Δ. Операция F является нелинейной, поэтому цифровые системы с квантованием процессов по времени и уровню относятся к классу нелинейных. Их особенности мы будем рассматривать отдельно в дальнейшем, а сейчас остановимся на линейных дискретных системах с процессами х(iТn), квантованными по времени.
| Рис. 1.3. Изображение дискретной системы | Рис. 1.4. Неоднозначность дискретной функции |
Работа дискретной системы сводится к преобразованию входных процессов x(iTn) в выходные у(iТn) с некоторыми заданными условиями. Схематически это отображено на рис. 1.3. По характеру желаемого преобразования дискретные системы подразделяются на те же классы, что и непрерывные, то есть на следящие, стабилизирующие, интегрирующие и др., однако возможности преобразования процессов в них имеют свои характерные особенности, которые мы и рассмотрим. Главной особенностью дискретных процессов x(iTn) является их неоднозначность. Заключается она в том, что одним и тем же дискретным процессам может соответствовать множество различных огибающих. Для примера на рис. 1.4 показаны две функции x1(t) и x2(t), которым соответствует один и тот же процесс х(iТn). Неоднозначность дискретных функций, в частности выходного процесса у(iТn) системы (рис. 1.3), может привести к неправильным выводам по результатам работы системы, поэтому предварительно должны быть изучены те условия, при которых возникающая неоднозначность была бы сведена к минимуму. Возникновение неоднозначности является следствием потери информации на интервалах между моментами квантования. Рассмотрим подробнее, как это происходит. Пусть квантованию с периодом Tn и частотой
подвергается гармонический процесс х(t) = a cos ωt.
Найдем зависимость между частотой исходного процесса и частотой огибающей ω0 квантованного процесса х(iTn). Первоначально положим, что частота ω 2
При ω > на каждый полупериод будет приходиться меньше одного значения x(iTn), что приведет к неоднозначности в определении ω. Так, если взять ω = Ω, то частота огибающей выходного процесса, как это видно из рис. 1.5, в, будет равна ω0 = 0, это и показано на рис. 1.6.
При ω = 3Ω/2 (рис. 1.5, г) мы получим дискретный процесс, совпадающий с x(iTn) при ω = (рис. 1.5, б). Подобные рассуждения можно продолжить и показать, что оценка частоты ω исходного процесса по частоте огибающей ω0 дискретного процесса будет неоднозначной. График этой зависимости изображен на рис. 1.6. Однозначность сохраняется лишь в диапазоне
1.3. Линейные разностные уравнения
Перейдем к математическому описанию линейных дискретных систем с помощью так называемых разностных уравнений. По своей структуре эти уравнения во многом напоминают дифференциальные уравнения непрерывных систем. Чтобы эта аналогия была более полной, рассмотрим вначале понятия о конечных разностях, для чего изобразим на рис. 1.7 дискретную функцию х(iТn). Нулевой конечной разностью называется само значение дискретной функции и обозначается через
Это понятие аналогично нулевой производной непрерывной функции.
Первой конечной разностью называется выражение
Рис. 1.7. Определение конечных разностей
Вторая разность равна разности первых разностей:
Третья разность равна разности вторых разностей:
и, в общем случае, разность k-го порядка
Этой разности можно сопоставить понятие k-й производной непрерывной функции. k-ю разность можно выразить через значения дискретной функции следующим образом:
Разностное уравнение дискретной системы устанавливает соответствие между входным и выходным дискретными процессами и их разностями. Линейным системам соответствует линейное соотношение между этими переменными, которое имеет вид:
Уравнение (1.5) называется линейным конечно-разностным уравнением и по своей структуре соответствует линейному дифференциальному уравнению (1.4). Коэффициенты и определяются параметрами системы, в том числе они зависят от периода повторения Tn. Если параметры системы не зависят от времени, то коэффициенты уравнения (1.5) будут постоянными и система называется стационарной. В дальнейшем, впредь до особых оговорок, займемся изучением только стационарных систем. Максимальный порядок п разности выходного процесса называется порядком уравнения или порядком дискретной системы.
Решение разностного уравнения можно записать в виде суммы
которая состоит из дискретного переходного процесса yn(iTn) и вынужденного процесса yx(iTn). Переходный процесс находится из решения однородного уравнения
где коэффициенты с и b определяются коэффициентами и уравнения (1.5). В уравнение (1.8) вошли входная и выходная переменные с учетом их запаздывания на конечное число периодов. Уравнения такого вида называются разностными в рекуррентной форме записи. Для объяснения такого названия выразим из уравнения (1.8) значение выходной переменной
Очевидно, что полученную формулу можно рассматривать как алгоритм вычисления выходной переменной по значениям входной переменной в m предшествующих моментах времени и (n-1) значениям выходной переменной, найденным на предыдущих этапах вычислений. Такая методика носит название рекуррентной, откуда и следует название уравнения.
Так как уравнения (1.5) и (1.8) по своему содержанию подобны, то решение рекуррентного уравнения полностью совпадает с решением (1.6) конечно-разностного уравнения. При этом переходный процесс находится из решения однородного уравнения
Предположим, что дискретная система описывается конечно-разностным уравнением второго порядка
| ^ C0 | y(iTn) + | ^ C1 | Δ1 y(iTn) + | ^ C2 | Δ2 y(iTn) = | ^ b0 | x(iTn). |
Составим уравнение в рекуррентной форме, для чего воспользуемся выражениями конечных разностей (1.1) и (1.2). Левая часть уравнения запишется в виде
получаем уравнение второго порядка в рекуррентной форме
Выразим в явном виде значение выходной переменной
Пусть огибающая входного процесса является линейной функцией
тогда дискретная функция равна
Найдем несколько значений выходного процесса при нулевых начальных условиях
Полагая i = 1, находим значение выходной переменной на первом шаге
Взяв i = 2, находим значение на втором шаге
По такой же схеме можно последовательно вычислять значения выходной переменной и в другие моменты времени.
1.4. Дискретное преобразование Лапласа
Одним из наиболее распространенных методов анализа линейных дискретных систем является операторный метод, основанный на дискретном преобразовании Лапласа, которое по своим возможностям и методике применения близко к преобразованию Лапласа для непрерывных функций.
Дискретным преобразованием Лапласа (ДПЛ) от функции х(iTn) называется сумма
Рассмотрим основные свойства дискретного преобразования Лапласа, которые будут использоваться при дальнейшем изложении.
а) ДПЛ обладает свойством периодичности, заключающемся в том, что
Так как ΩTn = 2π, то сомножитель
поскольку произведение целых чисел ki, в свою очередь, дает целое число. Таким образом, получаем
что и требовалось доказать.
Свойство периодичности говорит о том, что функция х*(р) располагается на комплексной плоскости р периодически относительно мнимой оси Im p с периодом jΩ (рис. 1.8).
Рис. 1.8. Главная полоса комплексной плоскости
Для изучения функции х*(р) достаточно рассматривать лишь главную полосу в пределах
(рис. 1.8), поэтому обратное дискретное преобразование Лапласа
имеет область интегрирования только в пределах главной полосы.
б) Связь между изображением х*(р) дискретной функции и изображением х(р) непрерывной огибающей имеет вид
Докажем это соотношение, для чего предварительно рассмотрим некоторые свойства бесконечной периодической последовательности дельта-функций, следующих с периодом Tn
Как и всякую периодическую функцию ее можно разложить в ряд Фурье и представить в виде бесконечной суммы гармонических составляющих
где комплексная амплитуда k-й гармоники
Так как интегрирование ведется в пределах
то из всей последовательности дельта-функций в этот предел попадает лишь центральное слагаемое при i = 0, а поэтому
Подставляя это равенство в формулу (1.14), получаем ряд Фурье в виде
Теперь найдем, чему равен интеграл от произведения функций:
Здесь при замене местами суммирования и интегрирования нижний предел суммирования принят равным нулю, так как функция x(t) берется в пределах от нуля до бесконечности. Выражение (1.15) дает связь между изображением дискретной функции х*(р) и непрерывной огибающей x(t). Подставим в это выражение вместо Δ (t) ее разложение в виде ряда Фурье и получим
Получающееся при этом выражение
Так как комплексная переменная p меняется в пределах
то новая переменная z будет находиться в диапазоне
| e | – j Ω 2 | ≤ z ≤ e | j Ω 2 | . |
В этих пределах модуль |z| = 1, а аргумент
поэтому интегрирование в плоскости z будет идти вдоль окружности единичного радиуса. После всех подстановок получим формулу обратного z-преобразования
где символически обозначен путь интегрирования вдоль окружности еди-ничного радиуса. Продолжим изучение свойств ДПЛ уже в форме z-преобразования.
в) Изображение функции х[(i- k)Tn] с запаздывающим аргументом kTn равно
Для доказательства запишем z-преобразование от рассматриваемой функции
где использована замена переменной i-k = r или i = r+k. С учетом того, что функция x(iTn) рассматривается только при положительном времени iTn, нижний предел суммирования можно заменить нулем и записать
что и доказывает соотношение (1.17).
г) Изображение разности k-ro порядка равно
Докажем это равенство. Используя формулу (1), запишем изображение первой разности
Из формулы (1.2) для второй разности получаем
Проделав такую же операцию над третьей разностью (1.3), можно по индукции убедиться в справедливости общего соотношения (1.18).
Убедимся в этом на нескольких конкретных примерах. В простейшем случае дискретная функция состоит из одной дискреты единичной амплитуды, расположенной в момент времени t = kTn (рис. 1.9, а).
Рис. 1.9. Примеры дискретных функций
Такую функцию будем называть единичным дискретным импульсом со следующими свойствами:
| δ [(i-k)Tn] = | < | 1 при i = k |
| 0 при i ≠ k | ||
Найдем изображение этой функции, пользуясь формулой (1.16):
Если единичный дискретный импульс расположен в начале координат (k = 0), то его изображение
Теперь положим, что непрерывная огибающая является единичной функцией
Тогда соответствующая ей функция х(iТn) называется единичной дискретной функцией (рис. 1.9, б) и равна
где учтено значение суммы бесконечной геометрической прогрессии
В заключение найдем изображение дискретной экспоненциальной функции
(рис. 1.9, в). Из формулы (1.16) следует, что
где также учтена сумма бесконечной геометрической прогрессии. Изображения для некоторых других дискретных функций приводятся в табл. П. 2. Полученные результаты и данные таблицы подтверждают правильность вывода о рациональном характере функции x*(z).
Запись изображения в виде (1.19) позволяет рекуррентным способом вычислять значения оригинала х(iTn) по изображению х*(z). Для этого перепишем выражение (1.19) в другом виде
По индукции можно получить следующую формулу для значения процесса в произвольный момент iTn
Особенность этого выражения состоит в последовательном (рекуррентном) вычислении переменных, начиная с первого периода следования.
е) Установившееся значение дискретной функции определяется по формуле
Изображение дискретной функции можно представить в виде предела
а функции с запаздыванием на один период
которое и доказывает свойство ( 1.20).
Z-преобразование является основным математическим аппаратом ис-следования линейных стационарных дискретных систем и поэтому широко используется в дальнейшем изложении.
1.5. Частотный спектр дискретного процесса
Заменяя в формуле (1.10) дискретного преобразования Лапласа переменную р на jω, получаем дискретное преобразование Фурье
которое определяет частотный спектр дискретного процесса. Чтобы получить спектр из формулы z-преобразования ( 1.16), надо ввести замену переменной
Изучим структуру спектра дискретного процесса, для чего воспользуемся формулой связи (1.13) между изображением х*(р) дискретной функции и ее огибающей. Произведя замену переменной р на jω, находим спектр дискретного процесса в виде
Таким образом, спектр дискретного процесса является периодической функцией частоты с периодом
составляющие которой пропорциональны спектру непрерывной огибающей с масштабом 1/Tn. Покажем на графиках характер амплитудно-частотного спектра дискретного процесса |x*(jω)| для следующих двух случаев.
и тогда в соответствии с формулой (1.21) спектр дискретного процесса примет вид, изображенный на нижнем рис. 1.10, а, и характерный наличием отдельных составляющих, совпадающих по форме с |x*(jω)|. Такая форма спектра называется гребенчатой. Во втором случае положим, что
и тогда спектр примет вид, показанный на рис. 1.10, б, где составляющие спектра перекрываются. По теореме Котельникова, о которой говорилось выше, для восстановления огибающей по дискретным данным о ней требуется выполнение условия
что соответствует спектру на рис. 1.10, а.
Рис. 1.10. Частотный спектр дискретного процесса
Таким образом, частота квантования Ω полезного сигнала должна выбираться так, чтобы спектр дискретного процесса был гребенчатым. Такому же условию должен удовлетворять и спектр выходного процесса у*(jω), что накладывает определенные требования на выбор структуры и параметров дискретной системы. Эти требования рассматриваются ниже.
1.6. Динамические характеристики
Возьмем z-преобразование от обеих его частей с учетом правила нахождения изображения конечной разности. В итоге получим операторное уравнение
из которого находим передаточную функцию дискретной системы в виде отношения изображений
ему будет соответствовать операторное уравнение
После преобразований получим вторую форму записи передаточной функции
Формулы (1.22) и (1.23) эквивалентны и могут быть получены друг из друга. С их помощью изображение выходного процесса по изображению входного процесса находится как произведение
Рис. 1.11. Соединение дискретных звеньев
Благодаря одинаковой структуре передаточной функции дискретной системы и передаточной функции непрерывной системы остаются справедливыми все правила структурных преобразований, применяемые для непрерывных систем. Так, для последовательного соединения дискретных звеньев (рис. 1.11,а)
Для параллельного соединения (рис. 1.11,б)
Для соединения с обратной связью (рис. 1.11, в)
| K * yx(z) = | K * 1(z) 1 ± K * 1(z) K * 2(z) |
Рис. 1.12. Импульсная характеристика дискретной системы
При нахождении временных характеристик в качестве типовых воздействий используются единичный дискретный импульс и единичная дискретная функция. Импульсной характеристикой линейной дискретной системы Kyx(iTn) (рис. 1.12, а) называется реакция на единичный дискретный импульс δ(iTn) при нулевых начальных условиях. С ее помощью можно определить реакцию системы на произвольное воздействие х(iTn). Рассматривая рис. 1.12,б, нетрудно понять, что значение выходного процесса y(iTn) можно подсчитать по формуле
| y(iTn) = | ∞ Σ k = 0 | x(kTn) kyx [(i-k)Tn]. |
Если учесть условие физической реализуемости импульсной характеристики
Мы искусственно домножили слагаемые на единичный множитель в форме
Поменяем местами порядок суммирования, произведем перегруппировку сомножителей и заменим переменную i-k = r, i = k+r, после чего будем иметь
поэтому изображение выходной переменной станет равным
Сравнивая это равенство с формулой (1.24), получаем выражение для передаточной функции через импульсную характеристику в виде
Таким образом, передаточная функция дискретной системы является z-преобразованием от импульсной характеристики.
Рис. 1.13. Переходная характеристика дискретной системы
Переходной характеристикой линейной дискретной системы hyx(iTn) называется реакция на единичную дискретную функцию 1(iTn) при нулевых начальных условиях (рис. 1.13). Подставляя в формулу свертки (1.25) функцию
найдем связь между переходной и импульсной характеристиками в виде
Переходная характеристика находится в виде суммы значений импульсной характеристики. Так как изображение единичного воздействия согласно табл. П. 2 равно
то изображение переходной характеристики
Перейдем к рассмотрению частотных характеристик, для чего в передаточной функции K * yx(z) заменим переменную
и обозначим полученную функцию через K * yx(z). Форму частотной характеристики дискретной системы удобнее всего получить, если вначале рассмотреть непрерывную огибающую kyx(t) импульсной характеристики kyx(iTn). На рисунке 1.12, а эта огибающая показана пунктиром. Возьмем преобразование Лапласа от этой непрерывной функции и назовем ее передаточной функцией системы по огибающей
Тогда в соответствии с формулой связи (1.13) между изображениями дискретной и непрерывной функций можно записать, что
Заменяя в этом равенстве p на jω, получаем формулу связи между частотными характеристиками дискретной системы и частотной характеристикой по огибающей
Рис. 1.14. Амплитудно-частотные характеристики инерционных дискретных звеньев
в передаточной функции К*(z). Особенность этих выражений состоит в том, что параметр τ в них является безразмерной величиной, поскольку оператор
также не имеет размерности. Называть поэтому параметр τ постоянной времени можно лишь условно. Несмотря на указанное отличие, между типовыми дискретными и непрерывными звеньями существует глубокая аналогия, которая наглядно видна при сравнении частотных характеристик. Напомним, что для получения частотной характеристики дискретной системы надо в передаточной функции К*(z) заменить
а это приводит к практически полному совпадению с частотными характеристиками типовых непрерывных звеньев с постоянной времени
Таким образом, в области ω, близких к нулю, частотные характеристики дискретных совпадают с характеристиками соответствующих непрерывных звеньев. Так, например, при ω = 0 частотная характеристика суммирующего (дискретного интегрирующего) звена равна
Рис. 1.15. Амплитудно-частотные характеристики разностных дискретных звеньев
1.8. Частотные характеристики и структурная схема дискретной следящей системы
Дискретная следящая система (рис. 1.16) предназначена для воспроизведения задающего воздействия х(iТn), и в идеальном случае выходной процесс в ней должен равняться входному, то есть
Выполнению этого равенства препятствуют два фактора: наличие возмущающих воздействий и инерционность системы. Оба эти фактора существенно влияют на выбор формы частотной характеристики замкнутой системы.
Рис. 1.16. Линейная дискретная следящая система
Частотный спектр задающего воздействия х*(jω) расположен в области низких частот и имеет граничную частоту ωгр ( рис. 1.17). В соответствии с теоремой Котельникова, частота квантования сигнала должна удовлетворять условию Ω > ωгр.
Рис. 1.17. Амплитудно-частотная характеристика дискретной следящей системы
Рис. 1.18. Амплитудно-частотная характеристика гребенчатого фильтра
Чтобы получить заданную K * yx(jω), надо сформировать вполне определенную частотную характеристику разомкнутой системы (рис. 1.16) K * (jω). Очевидно, что требования к последней аналогичны тем требованиям, которые предъявляются к частотным характеристикам разомкнутых непрерывных следящих систем. Так, чтобы обеспечить равенство
на частотах ω = 0 и ω, кратных Ω (см. рис. 1.18), необходимо иметь K * (jω) → 0, что достигается включением в состав системы суммирующих (дискретных интегрирующих) звеньев или усилительных звеньев с очень большим коэффициентом усиления. Чтобы обеспечить условие K * yx(jω) → 0 при ω → в состав разомкнутой системы надо включать инерционные (апериодические или колебательные) звенья. Согласование хода частотных характеристик в указанных областях может быть обеспечено разностными (дискретными дифференцирующими) звеньями.
Анализ частотных характеристик показывает, что структура дискретной следящей системы, определяемая звеньями, входящими в состав разомкнутой системы, аналогична структуре непрерывных следящих систем и соответственно аналогичны и передаточные функции сравниваемых систем. Передаточная функция дискретной разомкнутой следящей системы (рис. 1.16), например, может быть получена из разностного уравнения, записанного в конечно-разностной форме
Передаточная функция замкнутой системы, получаемая из формулы (1.30) или по рис. 1.16, оказывается равной
где полином знаменателя
В следящих системах ошибка e(iTn) совпадает с рассогласованием r(iTn) и, следовательно, передаточная функция ошибки по задающему воздействию согласно рис. 1.16 равна
Передаточная функция ошибки по возмущающему воздействию, как и в непрерывных системах, равна
то есть с точностью до знака совпадает с передаточной функцией системы по этому воздействию и согласно рис. 1.16 равна
Отметим, что если исходное уравнение разомкнутой следящей системы (1.28) записывается в рекуррентной форме (см. п. 1.3)
то уравнение замкнутой примет вид
При этом полиномы P*(z), Q*(z) и D*(z) меняют свою структуру и передаточные функции дискретной следящей системы записываются в следующем виде:
1.9. Структурная схема цифровой следящей системы
Использование цифровых методов обработки информации в системах автоматического управления позволяет реализовывать сложные алгоритмы управления и обеспечивать их быструю сменяемость. Кроме того, цифровые устройства, как правило, более надежны в работе и имеют меньшие габариты и массу. Автоматические системы, полностью построенные на цифровых элементах, называются цифровыми САУ (ЦСАУ). Особенно широкое распространение ЦСАУ получили в радиотехнических системах для обработки информации о параметрах радиосигналов. Например, в радиолокационных системах эти параметры (амплитуда, частота, фаза и др.) несут информацию о координатах объектов, поэтому в них используют ЦСАУ для слежения за угловыми координатами, дальностью и скоростью перемещения целей. В радиотехнических следящих системах входная информация передается с помощью радиосигналов, а выходная, как правило, в виде электрических сигналов, что дает возможность выполнить систему только из электронных элементов и устройств. В том случае, когда выходная информация должна выдаваться в виде линейных или угловых перемещений, используют электрические и электромеханические цифровые элементы. Сигналы в ЦСАУ формируются в виде последовательности импульсов, образующих некоторый код, с помощью которого записываются мгновенные значения процессов, подлежащих обработке.
Кодовая модуляция сигналов приводит к тому, что информация в системе квантуется как по времени, так и по уровню. Квантование по времени происходит из-за импульсного “характера сигналов, в результате чего полезная информация выдается в виде дискретной функции x(iTn). Квантование по уровню происходит за счет конечного числа импульсов в коде, называемого числом разрядов. При конечном числе разрядов можно отобразить лишь конечное число дискретных значений передаваемого процесса. Например, в случае двоичного кода при числе разрядов q максимальное число дискретных значений процесса
Так, если код имеет 8 разрядов, то N = 225; если q = 12, то N = 4095. При заданном числе разрядов передаваемый процесс x(iTn) может отображаться не более чем N дискретными значениями.
Рис. 1.19. Два способа квантования по уровню
Если максимальное значение процесса равно xmах, а минимальное xmin, то шаг квантования по уровню
В результате квантования по уровню получается процесс (iTn), который будет лишь приближенно отражать характер изменения процесса x(iTn). Ошибка приближения (округления) будет зависеть от шага квантования и способа квантования по уровню, два из которых показаны на рис. 1.19. В первом случае квантование по уровню происходит по правилу: принимается значение (iTn), ближайшее к x(iTn) (рис. 1.19, а). Во втором принимается значение (iTn), ближайшее к x(iTn) снизу для x(iTn) > 0 и сверху для x(iTn) Tn
должна удовлетворять теореме Котельникова (п.1.2), то быстродействие ЦВМ может существенно влиять на качество работы системы. Время обработки информации машиной Т0 складывается из времени ввода и вывода данных, времени обращения к памяти и времени проведения операций в процессоре. При работе в реальном масштабе времени
За время T0 = α Tn информация обрабатывается в соответствии с заложенными в машину алгоритмами, которые задаются в виде разностных уравнений. Если эти уравнения линейные, например вида (1.5) или (1.8), то алгоритму будет соответствовать передаточная функция K * α(z), которая в виде дискретного звена должна отображаться на структурной схеме.
Рис. 1. 24. Структурная схема цифровой следящей системы
В том случае, когда период квантования Tn определяется только быстродействием ЦВМ, можно полагать α = 1, а если время обработки T0 i k, (2.1)
– переходная составляющая, представляющая собой сумму экспоненциальных дискретных функций
называемой билинейным или w-преобразованием. Если комплексное число w представить в алгебраической форме
то условие устойчивости дискретной системы |zk| 2
Введение билинейного преобразования (2.2) позволяет использовать для анализа устойчивости дискретных систем алгебраические и частотные критерии устойчивости непрерывных систем. Методика решения задачи рассматривается на примере.
Передаточная функция разомкнутой следящей системы (рис. 1.15) задана в виде
то есть система состоит из запаздывающего и суммирующего звеньев. Определим условия устойчивости замкнутой дискретной системы, используя способы, описанные выше.
1. Непосредственное решение разностного уравнения.
Для замкнутой системы получаем
Разностное уравнение в z-изображениях
Однородное разностное уравнение в оригиналах, определяющее переходную составляющую:
Решение этого уравнения при
записывается в виде
в формулу (2.8), получим характеристическое уравнение замкнутой системы в виде
получим выражение для исходной передаточной функции разомкнутой системы
Если по аналогии с непрерывными системами, где вводится замена p = jω, подставить в выражение (2.9) w = jν, то можно построить частотные характеристики разомкнутой дискретной системы и по ним судить об устойчивости замкнутой системы. Для использования логарифмического критерия на рис. 2.5 построены ЛЧХ, соответствующие выражению (2.9).
Рис. 2.5. Логарифмические характеристики дискретной системы при различных коэффициентах преобразования
На рис. 2.5 показаны ЛАХ системы для k 2. Согласно, логарифмическому критерию замкнутая система будет устойчивой только при k / 2 2
| ω = | Ω 2 | , где Ω = | 2 π Tn | . |
Приведенный пример показывает, что все способы оценки устойчивости дают одинаковые результаты. Выбор способа зависит от сложности системы, исходного материала и необходимого вида получаемых данных. Для оценки устойчивости с помощью критерия Гурвица в табл. П.3 приведены расчетные соотношения, связывающие условия устойчивости дискретных систем с коэффициентами характеристического уравнения
Степень устойчивости в дискретных системах, как и в теории непрерывных систем, оценивается по степени удаления корней характеристического уравнения D*(z) = 0 от линии круга единичного радиуса (рис. 2.2). Косвенной оценкой степени устойчивости и здесь служат запасы устойчивости по фазе Δφ(νc) и амплитуде ΔL (см., например, рис. 2.5). Отметим одну особенность, характерную только для дискретных систем. Пусть передаточная функция системы описывается соотношением
В отличие от непрерывных систем в дискретных можно (по крайней мере, в принципе) подобрать параметры системы так, чтобы все коэффициенты ci характеристического уравнения D*(z) = 0 кроме с0, равнялись нулю. В этом случае (2.10) примет вид
| K * yx(z) = | P*(z) c0 | , (2.11) |
2.2. Качество дискретных систем в переходном режиме
Переходная характеристика замкнутой системы hyx(iTn) определяется как реакция этой системы на дискретную единичную функцию (рис. 2.6)
Рис. 2.6. Структурная схема дискретной системы
Она может быть вычислена непосредственно по разностному уравнению
при нулевых начальных условиях или с помощью любого из приемов определения обратного z-преобразования от изображения
Вычислим для условий примера 2.1 переходную характеристику, воспользовавшись двумя указанными способами.
1. Разностное уравнение в z-изображениях для переходной характеристики записывается из выражения (2.6)
или в оригиналах при x(iTn) = 1(iTn)
С другой стороны, по определению
и, следовательно, можно записать
Сравнивая коэффициенты при одинаковых степенях z в левой и правой частях равенства, нетрудно получить значения hyx(iTn), совпадающие с результатом решения уравнения (2.15).
В подразделе 2.1 отмечалось, что при выполнении условий бесконечной степени устойчивости переходный процесс в системе заканчивается за конечное, вполне определенное число периодов Tn. Покажем, что это выполняется и для переходной характеристики, учитывая, что указанные условия имеют место, если все коэффициенты характеристического уравнения замкнутой системы D*(z) = 0 кроме c0, равны нулю, то есть передаточная функция соответствует выражению (2.11). В этом случае согласно (2.13)
где принято обозначение
Сравнивая теперь коэффициенты при одинаковых степенях z, можно получить
Таким образом, при бесконечной степени устойчивости переходная характеристика принимает установившееся значение за конечное число периодов m (рис. 2.8), количественно равное порядку полинома числителя передаточной функции системы. Так, в рассмотренном примере, условие бесконечной степени устойчивости k = 1 [см. формулу (2.5)], при этом согласно выражению (2.15)
и переходная характеристика принимает установившееся значение за один период.
Рис. 2.8. Переходная характеристика при бесконечной степени устойчивости
Рассмотрим последовательность вычисления суммарной оценки:
1) находится z-изображение ошибки
Рис. 2.9. Ошибки дискретной системы
2) по выражению (1.20) для конечных значений (подраздел 1.4) определяется установившееся значение ошибки
4) с помощью таблиц интеграла Парсеваля определяется квадратичная суммарная оценка
Отметим, что при вычислении e*пер(z) знак разности может получиться как положительным, так и отрицательным, что при дальнейших вычислениях не принимается во внимание, так как рассчитывается квадратичная оценка. Отметим также, что в формуле (2.16) вместо ошибки e(iTn) могут быть использованы выходные y(iTn) или какие-либо другие координаты системы, если их установившиеся значения легко вычисляются.
Определить квадратичную суммарную оценку качества переходного режима в системе для условий примера 2.1, полагая, что на вход замкнутой системы (рис. 1.16) подаются:
1) дискретная единичная функция x(iTn) = x0 1(iTn) или
2) дискретная линейная функция x(iTn) = x1 iTn или
Здесь z-изображения записаны на основании табл. П.2. для огибающих x(t) = x01(t) и x(t) = x1t. В рассматриваемом примере
и, следовательно, передаточная функция ошибки
z-изображение ошибки в случае дискретной единичной функции
Установившееся значение ошибки
Изображения переходной составляющей ошибки
Табулированный интеграл для l = 1 (табл. П.1) равен
и квадратичная суммарная оценка
Для случая дискретной линейной функции аналогично получим
В обоих случаях Q* принимает бесконечные значения при k = 0 и k = 2, соответствующим границе устойчивости системы (пример 2.1) и теряет смысл (становится отрицательной) при k 2, когда система неустойчива. При k = 1 (бесконечная степень устойчивости) квадратичная суммарная оценка в обоих случаях минимальна.
2.3. Качество дискретных систем в установившемся режиме при регулярных воздействиях
После окончания переходных процессов в системе наступает установившийся режим, качество которого в основном зависит от точности отработки задающих воздействий и степени фильтрации помех. В теории дискретных систем удобным способом оценки качества является оценка точности, то есть анализ ошибок управления. Эти ошибки зависят от параметров системы, ее структуры, от характеристик воздействий и в плане математическом определяются вынужденной составляющей решения разностного уравнения
| yв(iTn) = yx(iTn) + | M Σ j = 0 | yνj(iTn), |
Для следящих систем ошибка управления представляет собой разность
то есть в установившемся режиме она равна
| e(iTn) = ex(iTn) + | M Σ j = 0 | yνj(iTn), (2.17) |
Оценка качества установившегося режима производится по значению ошибки (2.17) или некоторых функций от нее и имеет особое значение, так как у большинства систем (в том числе у всех следящих) этот режим является основным, определяющим выполнение системой поставленной задачи. Как и в теории непрерывных систем, исследование точности дискретных систем в установившемся режиме производят для регулярных и случайных процессов, описывающих как задающие, так и возмущающие воздействия. Регулярными функциями времени можно аппроксимировать некоторые виды задающих и возмущающих воздействий или их математические ожидания.
Методика расчета ошибок при регулярных воздействиях справедлива (при определенных предпосылках) для процессов любого происхождения, поэтому рассмотрим ее на примере оценки качества дискретной системы при регулярных задающих воздействиях x(iTn), имея в виду и тот факт, что такими воздействиями часто аппроксимируют процессы, соответствующие наиболее тяжелому или наиболее вероятному режимам работы. Будем полагать, таким образом, что известными являются закон изменения x(iTn), структура и параметры дискретной следящей системы (рис. 1.16), то есть ее передаточная функция K*(z).
Установившееся значение ошибки
может быть найдено по z-изображению e*(z) как
или для рассматриваемой системы (рис. 1.16)
Понятно, что при z = l функция K * ν(z) примет значение, равное коэффициенту преобразования разомкнутой системы
и, следовательно, формулу (2.20) можно записать в виде
позволяющем определять eуст для системы с различным порядком астатизма при воздействиях типа
установившаяся ошибка в системе принимает значение
Если такой же сигнал подать на систему с астатизмом первого порядка (ν = 1), то
Аналогично можно показать, что при подаче сигналов x(t) = x1(t) и x(t) = x01(t) на систему с астатизмом второго порядка (ν = 2) установившаяся ошибка будет равна нулю. Если воздействие задано в виде
| x(t) = | 1 2 | x2 t 2 или x(iTn) = | 1 2 | , |
Полученные результаты нетрудно обобщить на системы любого порядка астатизма и убедиться, что при подаче на систему с астатизмом ν-го порядка воздействия вида
установившаяся ошибка будет равна
Системы астатические ν-го порядка не будут иметь ошибок установившегося режима при подаче на них воздействий вида
если ν1 * ex(z) (1.32) представляется в виде ряда
который сходится, если z → 1 (i → ∞), то есть если рассматривается установившийся режим. Так как
то из выражения (2.19) можно определить изображение ошибки
и тогда формулу (2.19) можно записать следующим образом:
Сравнивая в выражении (2.22) коэффициенты при одинаковых степенях χ, нетрудно определить
Структурная схема следящей системы показана на рис. 1.16. Полагая, что
оценим точность системы в установившемся режиме, если огибающая задающего воздействия х(iTn) аппроксимируется функцией
Определим вначале конечные разности дискретного задающего воздействия
Согласно методике, изложенной в п. 1.4, получаем
Определим коэффициенты ошибок, для чего запишем
Введем подстановку (2.21) и получим
Этот же результат можно получить и по формуле (2.23) для
Ряд ошибки (2.20) для рассматриваемого примера запишется в виде
Установившаяся ошибка нарастает со временем за счет ускорения сигнала (2.24), не компенсируемого системой с одним дискретным интегратором. Это нарастание тем интенсивнее, чем больше период Tn и ускорение x2 и чем меньше коэффициент преобразования, который по условиям устойчивости (см. пример 2.1) меняется в пределах 0 k
Этот результат для систем с астатизмом первого порядка получен в начале подраздела.
2.4. Статистический анализ точности в установившемся режиме
Математическое ожидание представляет собой регулярную функцию Времени, методика его определения показана в п.2.3. Случайная составляющая ошибки, как и в непрерывных системах, оценивается по величине ее дисперсии
Рассмотрим методику решения задачи в предположении, что все воздействия представляют собой эргодические стационарные процессы, статистически не зависящие друг от друга. В этом случае дисперсия ошибки
определяется из (2.19) соотношением
| De = Dex + | M Σ j = 0 | Deνj, |
Определение величины дисперсии дискретного процесса производится (как и в случае непрерывных систем) по его корреляционной функции, которая для стационарных процессов определяется как
Обратное z-преобразование от спектральной плотности определяет корреляционную функцию и поэтому