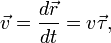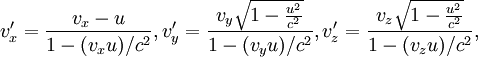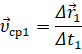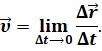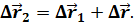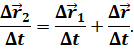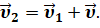какая скорость называется мгновенной

Мгновенная скорость – формула определения, уравнение

Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.

Скорость при неравномерном движении

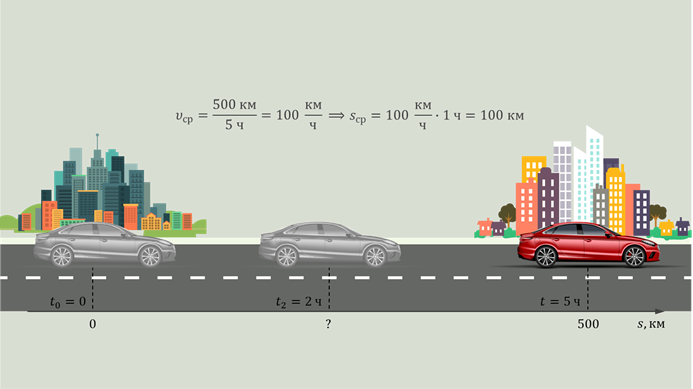
Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

Рис. 1. Скорость равномерного прямолинейного движения.

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.

В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:

Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.

Рис. 2. Стробоскопическое фото свободного падения.

Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.

Свести неравномерное движение к равномерному невозможно.

Мгновенная скорость

Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.

Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:

Источник

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

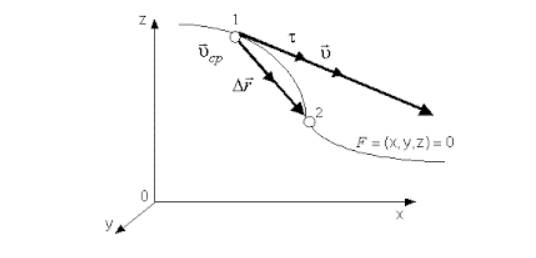
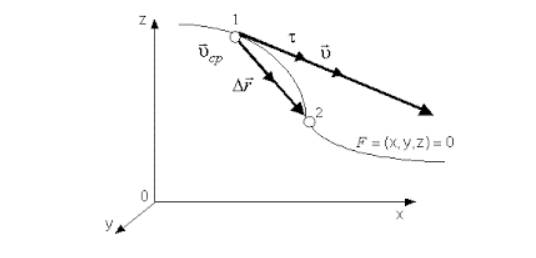
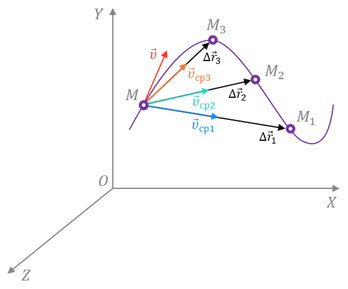
Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

Источник

Мгновенная скорость

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse ) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Содержание

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 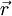этой точки:

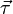
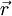
Здесь v — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Преобразование скорости

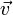
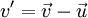
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

См. также

Полезное

Смотреть что такое “Мгновенная скорость” в других словарях:

мгновенная скорость — скорость; мгновенная скорость Скорость точки жидкости, рассматриваемая как векторная функция переменных Эйлера … Политехнический терминологический толковый словарь

мгновенная скорость — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN instantaneous speedinstantaneous velocity … Справочник технического переводчика

мгновенная скорость — akimirkinis greitis statusas T sritis automatika atitikmenys: angl. instantaneous speed vok. augenblickliche Geschwindigkeit, f; momentane Geschwindigkeit, f; Momentangeschwindigkeit, f rus. мгновенная скорость, f pranc. vitesse instantanée, f… … Automatikos terminų žodynas

мгновенная скорость — akimirkinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Greitis tam tikrą akimirką. atitikmenys: angl. instantaneous speed; instantaneous velocity vok. augenblickliche Geschwindigkeit, f; Momentangeschwindigkeit, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

мгновенная скорость — akimirkinis greitis statusas T sritis fizika atitikmenys: angl. instantaneous velocity vok. augenblickliche Geschwindigkeit, f; Momentangeschwindigkeit, f rus. мгновенная скорость, f pranc. vitesse instantanée, f … Fizikos terminų žodynas

МГНОВЕННАЯ СКОРОСТЬ РОСТА ПОПУЛЯЦИИ — скорость изменения числа организмов r в зависимости от времени в данный момент. Определяется по формуле: ║ где dN изменение числа организмов в данный момент времени dt; N число особей в популяции. См. также Мальтузианский параметр.… … Экологический словарь

мгновенная скорость фильтрования — Скорость фильтрования в данный момент времени. [ГОСТ 16887 71] Тематики фильтрование, центрифугирование, сепарирование … Справочник технического переводчика

мгновенная скорость ветра — 3.7 мгновенная скорость ветра: Скорость ветра в выделенной точке пространства скорость, которую имеет бесконечно малый объем воздуха, окружающий данную точку, характеризуется модулем и направлением. Источник: ГОСТ Р 54433 2011: Возобновляемая… … Словарь-справочник терминов нормативно-технической документации

Мгновенная скорость фильтрования — 57. Мгновенная скорость фильтрования Скорость фильтрования в данный момент времени Источник: ГОСТ 16887 71: Разделение жидких неоднородных систем методами фильтрования и центрифугирования. Термины и определения … Словарь-справочник терминов нормативно-технической документации

мгновенная скорость нагрева — Syn: мгновенная скорость нагревания … Металлургический словарь терминов

Источник

Мгновенная скорость. Сложение скоростей

Урок 4. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Мгновенная скорость. Сложение скоростей”

Самым простым видом механического движения является прямолинейное движение с постоянной по модулю и направлению скоростью:

Однако не будем забывать о том, что равномерно движение — это модель реального движения. В действительности же реальные тела чаще всего движутся не равномерно. Например, все вы знаете, что автомобиль в начале своего движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине пути он, возможно, будет недолго двигаться с постоянной скоростью. А при торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля является неравномерным. Поэтому описать его с помощью уравнения движения мы не можем, так как скорость тела постоянно меняется.

Но нам на помощь приходить понятие мгновенной скорости, то есть скорости точки в данный момент времени (или в данной точке траектории).

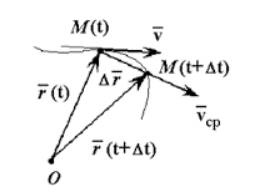
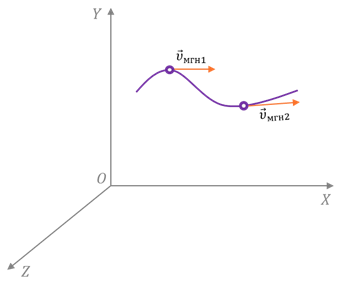
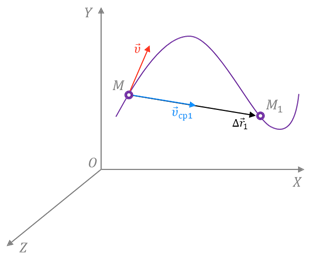
Чтобы понять, как определяется мгновенная скорость, рассмотрим неравномерное движение материальной точки по криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М. А спустя некоторый промежуток времени Δt₁ — положение М₁.

Укажем на рисунке перемещение, которое совершила точка за этот промежуток времени.

Если теперь мы с вами разделим это перемещение на промежуток времени, в течение которого оно произошло, то тем самым найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени. Эта скорость называется средней скоростью перемещения. Она показывает, какое перемещение в среднем совершала точка за единицу времени.

Направление этой скорости совпадает с направлением вектора перемещения точки.

Но как же нам определить скорость точки в положении М? Давайте попробуем уменьшить рассматриваемый промежуток времени. Из рисунка видим, что в этом случае точка совершит меньшее перемещение. Средняя же скорость точки на этом участке хотя и не равна скорости в точке М, но уже ближе к ней.

Если мы продолжим уменьшать промежутки времени и, соответственно, перемещения, то очень скоро мы придём к тому, что средние скорости будут незначительно отличаться друг от друга и от скорости точки в положении М. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время. Следовательно, при стремлении промежутка времени к нулю отношение 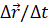будет стремиться к своему некоторому предельному значению.

Физическая векторная величина, равная пределу отношения перемещения к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенной скоростью:

Направление вектора мгновенной скорости зависит от вида движения точки. Так, если точка движется прямолинейно, то направление мгновенной скорости совпадает с направлением движения. А вот в случае криволинейного движения вектор мгновенной скорости направлен по касательной к траектории.

В этом легко убедиться, если понаблюдать за раскалёнными частицами, отрывающимися от точильного камня. Или за частицами грязи, вылетающими из-под колеса буксующего автомобиля.

Для описания неравномерного движения точки, помимо понятия средней скорости перемещения, в физике чаще используют понятие средней путевой скорости. Она определяется отношением пути к промежутку времени, за который этот путь пройдён:

Проще говоря, средняя путевая скорость показывает, какой путь в среднем проходило тело за единицу времени.

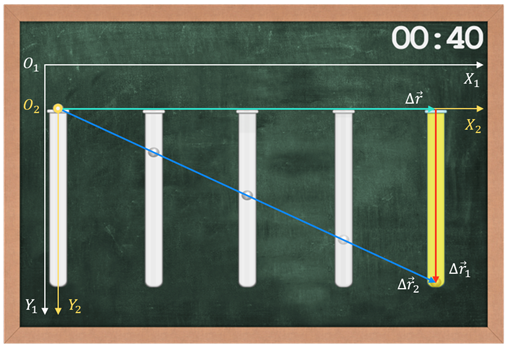
Однако не стоит забывать о том, что средняя путевая скорость характеризует движение за весь промежуток времени в целом. Например, когда мы слышим, что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью 100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но во время движения он мог заехать на заправку, где-то двигаться с бо́льшей или меньшей скоростью. Иными словами, средняя путевая скорость не даёт информации о скорости движения точки в каждый момент времени.

Для примера давайте с вами определим среднюю путевую скорость движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а вторую — со скоростью 25 м/с.

Мы уже с вами не раз говорили о том, что характер движения точки зависит от того, относительно каких тел мы рассматриваем это движение (то есть от выбора системы отсчёта). Но так как тело отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же тела можно одновременно рассматривать в разных системах координат.

Рассмотрим такой опыт. Пусть у нас есть стеклянная трубка, заполненная вязкой жидкостью. Опустим в неё тяжёлый шарик и будем перемещать трубку относительно школьной доски в горизонтальном направлении, не меняя ориентации трубки. Одновременно будем наблюдать за движением шарика и отмечать его положения через равные интервалы времени.

Теперь выберем две системы координат: одну свяжем с доской и назовём неподвижной, а вторую — с трубкой и назовём движущейся.

Из рисунка видно, что перемещение точки относительно неподвижной системы отсчёта равно векторной сумме её перемещения относительно движущейся системы и перемещения движущейся системы отсчёта относительно неподвижной:

В этом состоит принцип независимости движений.

Теперь разделим записанное нами уравнение на промежуток времени, в течение которого произошли эти перемещения:

И учтём, что отношения перемещений к промежутку времени равны скоростям:

Таким образом получаем, что скорость тела относительно неподвижной системы отсчёта равна векторной сумме его скорости относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.

Данное утверждение называется законом сложения скоросте́й Галилея. Он справедлив как для равномерного, так и для неравномерного движения. Только в этом случае складываются мгновенные скорости.

Однако этот закон нельзя применять для точек, движение которых происходит со скоростями, близкими к скорости света в вакууме.

Для примера решим такую задачу. На какой угол следует отклонится от перпендикуляра к течению реки и сколько времени нужно плыть на лодке, чтобы пересечь реку перпендикулярно её течению, если скорость лодки относительно воды 3 м/с, скорость течения реки — 1,5 м/с, а ширина русла — 400 м?

Источник

Кинематика. Скорость.

Скорость характеризует быстроту любых изменений в окружающем мире. Распространение звука или света в воздухе, движение облаков, испарение воды, полет птиц, движение пешеходов по улице – все явления характеризуются определенно скоростью.

Скорость – векторная физическая величина, характеризующая не только быстроту перемещения тела, но и направление его движения.

Скоростью точки называется предел отношения перемещения к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении Δt к нулю:

Такое определение скорости называют также мгновенной скоростью. Оно справедливо и для любых видов движения. Вектор мгновенной скорости всегда направлен по касательной к траектории движения, указывая направление, по которому происходило бы движение тела, если бы с момента времени t на него прекратилось действие других тел.

Понятие средней скорости вводится для характеристики неравномерного движения (движения с переменной скоростью). Определяется она скалярно или векторно.

Когда средняя скорость тела υ_ср равна отношению всего пути Δs ко всему времени движения Δt, то Здесь пройденный путь и время – скалярные величины, следовательно скорость тоже величина скалярная.

Когда средняя скорость тела равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло, то Здесь средняя скорость перемещения – векторная величина.

Для неравномерного криволинейного движения векторное определение средней скорости не всегда позволяет определить реальные скорости на пути движения тела. Например, при движении тела по замкнутой траектории в течение некоторого времени его перемещение равно нулю, хотя скорость была отлична от нуля. В таком случае лучше пользоваться скалярным определением скорости.

Источник