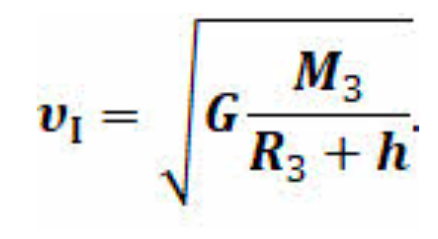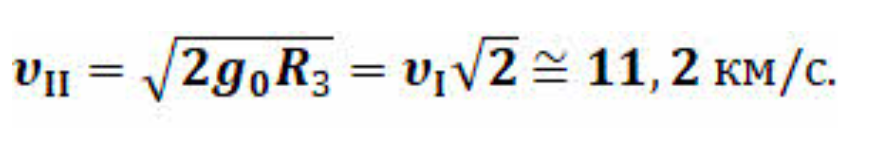какая скорость спутника в космосе
Проект 5. Скоростной спутник Земли
Барон: Я берусь создать спутник, который будет вращаться вокруг Земли со скоростью 30 километров в секунду! И при этом невесомости в корабле не будет!
Профессор: Но если скорость больше второй космической, спутник должен покинуть Землю навсегда!
Инженер: Если на вашем корабле работает двигатель, то почему же скорость не увеличивается?
Бизнесмен: А надолго ли хватит горючего?
Первая космическая скорость
Прежде чем приступить к обсуждению проекта барона, вспомним, что такое первая и вторая космические скорости. Для того чтобы заранее предвосхитить все возможные недоумения учащихся представим наши рассуждения в форме воображаемого диалога Автора с Читателем.
Автор: Как вы считаете, можно ли неограниченно долго падать на Землю и при этом. не упасть на нее?
Читатель: Думаю, нет. В конце концов, всё, что падает, упадет.
Автор: А как же искусственные спутники Земли? Они ведь всё время находятся в свободном падении.
Читатель: Спутники? Но они же вращаются вокруг Земли, а не падают на нее!
Автор: Под падением я понимаю движение под действием одной-единственной силы — силы тяжести. А на спутник с выключенными двигателями никакие другие силы как раз и не действуют. Так что движение спутника — это типичное свободное падение.
Читатель: Тогда я не понимаю, как же спутникам удается удержаться на орбите.
Автор: Вас удивляет, что сила тяжести тянет спутник к центру Земли, а он движется по окружности? А посмотрите на шарик, который вращают на нити в горизонтальной плоскости (рис. 5.1): сила натяжения нити всё время направлена к центру окружности, а шарик движется по окружности.
На спутник же вместо силы натяжения нити действует сила тяжести (рис. 5.2).
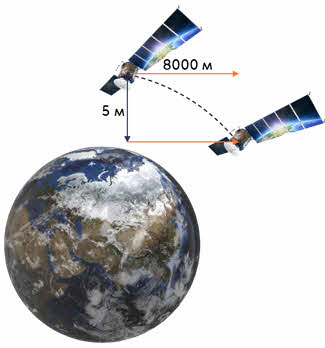
Чтобы было понятнее, проведем такой мысленный эксперимент. Поднимемся на очень высокую башню — высотой километров эдак в сто (на этой высоте сила сопротивления воздуха уже практически отсутствует) — и будем бросать с башни камешки, как показано на рис. 5.3. Чем с большей скоростью мы бросим камешек, тем дальше упадет он от основания башни. Наконец, при какой-то определенной скорости он вообще не упадет на землю, а вернется к нам с противоположной стороны.
Тут необходима осторожность: учитывая, что скорость такого камешка должна быть раз в 10 больше скорости артиллерийского снаряда, то последствия могут быть. сами понимаете. А скорость такого камешка как раз и называется первой космической. Сформулируем это четче.
Первой космической скоростью называется скорость, которую надо сообщить телу, чтобы оно стало спутником Земли и двигалось по круговой орбите на небольшой по сравнению с радиусом Земли высоте.
По второму закону Ньютона:
Подставим численные значения (R = 6,400·10 6 м, g = 9,8 м/с 2 ), получим:
Запомним: первая космическая скорость хI = 7,9 км/с.
Заметим, что по формуле (5.1) можно вычислить первую космическую скорость не только для Земли, но и для любой другой планеты.
Читатель: А если камешку на рис. 5.3 сообщить скорость х > 7,9 км/с?
Автор: При скорости, большей первой космической, траектория камешка (или космической станции) из окружности превратится в эллипс, который по мере увеличения скорости будет становиться всё более вытянутым (рис. 5.4). Наконец, при скорости х = 11,2 км/с, которую называют второй космической, траектория тела из эллипса превратится в параболу и тело навсегда покинет пределы земного тяготения.
Идея скоростного спутника
Теперь об идее барона. Скорость, с которой его спутник вращается вокруг Земли — 30 км/c — значительно больше первой космической скорости, которая, как мы с вами выяснили, составляет всего 7,9 км/c! Но у спутника барона, как видно из рисунка на плакате, имеется двигатель, который выбрасывает реактивную струю в направлении от центра орбиты! Этот двигатель создает дополнительную силу, которая теперь вместе с силой тяготения сообщает спутнику центростремительное ускорение. Иными словами, центростремительная сила увеличилась на величину силы тяги реактивного двигателя, а, значит, увеличилось и центростремительное ускорение. Теперь второй закон Ньютона для спутника будет иметь вид:
где f — реактивная сила, х — скорость спутника, R — радиус орбиты, m — масса спутника, а g — ускорение свободного падения (рис. 5.5).
Из формулы (5.2) ясно, что, увеличивая реактивную силу f, мы можем увеличивать скорость вращения спутника х. Теоретически нам никто не мешает сделать реактивную силу сколь угодно большой, а значит и скорость обращения спутника можно теоретически неограниченно увеличивать вплоть до скорости света. Проблемы начинаются там, где мы от теории переходим к практике.
Сначала ответим на возражение Профессора. Он опасается, что, поскольку скорость спутника превышает не только первую, но и вторую космическую, то наш спутник удалится от Земли на бесконечное расстояние. Профессор просто забыл, что это справедливо только для небесного тела — то есть спутника, не имеющего никаких двигателей. Наличие двигателя всё принципиально меняет. С двигателем можно улететь с Земли с любой, даже очень маленькой скоростью (если не жалко горючего), а можно и не улететь от нее далеко, двигаясь очень быстро!
Так что возражение Профессора мы не принимаем.
Теперь остановимся на возражении Инженера: почему не увеличивается скорость, если работает двигатель? То есть почему не увеличивается скорость, если на спутник действует сила?
Тут уместен контрвопрос: а почему не увеличивается скорость спутника, который движется вокруг Земли по круговой орбите с первой космической скоростью (см. рис. 5.2)? На него ведь тоже действует сила тяготения. А почему не увеличивается скорость шарика, который мы раскручиваем на веревке (см. рис. 5.1)? На него ведь тоже действует сила натяжения нити!
Дело в том, что все эти силы направлены перпендикулярно к направлению скорости, поэтому они не совершают механической работы: угол, который составляет каждая из этих сил с вектором малого перемещения, равен 90°, поэтому работа всех этих сил равна: А = F·Δs·cos90° = 0. И все эти силы «занимаются» не увеличением величины скорости тела, а изменением направления скорости.
Можно спросить: на что же тогда тратится энергия топлива, ведь она же не может исчезнуть? Увы, она тратится довольно расточительно — на увеличение внутренней энергии продуктов сгорания топлива.
Самый неприятный для барона вопрос задал Бизнесмен: «А сколько потребуется горючего?»
Не будем огорчать барона: очень много, лучше даже не рассчитывать, чтобы не расстраиваться. Двигатель должен работать на полную мощность постоянно, а ведь топливо еще надо доставить на орбиту! Правда, барон ничего не сказал о конструкции своего двигателя. Может быть, он уже научился черпать энергию «из физического вакуума», как предлагают некоторые современные изобретатели? Тогда другое дело!
Лучше сделаем другую оценку. Вычислим, какую перегрузку будет испытывать барон, если он окажется внутри собственного спутника. То есть вычислим, во сколько раз вес барона в спутнике будет больше его веса на Земле.
Заметим, что в спутнике барона невесомости нет — что, конечно, хорошо, если вес не слишком велик, и очень плохо, если вес становится слишком большим!
Итак, пусть наш барон имеет массу 100 кг и движется в своем спутнике по орбите радиусом 6400 км, то есть на околоземной орбите. Тогда ускорение свободного падения равно g = 9,8 м/с 2 (рис. 5.6). Скорость спутника v = 30 км/с.
На барона действуют две силы: сила реакции со стороны пола и сила тяготения. Запишем второй закон Ньютона в проекции на направление нормали 
:
, отсюда:
Ясно, что по третьему закону Ньютона с точно такой же по величине силой барон будет давить на пол:
В то же время на Земле вес барона, имеющего массу 100 кг, равен 100 кгс. Таким образом, вес барона в спутнике увеличится в 13 раз!
В истории космонавтики были случаи, когда в течение нескольких секунд космонавты выдерживали подобные перегрузки и при этом оставались живы. Но наш барон человек исключительной физической силы, поэтому, возможно, он выдержит несколько минут такого полета. Хотя, честно говоря, лучше бы сбросить скорость хотя бы до 20 километров в секунду: амбиции амбициями, а жизнь всё-таки дороже!
Космические скорости и межпланетные перелёты
На основании закона всемирного тяготения Ньютон первым теоретически обосновал возможность создания искусственного спутника Земли. Давайте вспомним, что искусственными спутниками называют космические аппараты, созданные людьми, которые позволяют наблюдать за планетой, около которой они вращаются, а также другими астрономическими объектами из космоса.
Чтобы понять, при каких условиях тело способно стать искусственным спутником Земли, обратимся к размышлениям Ньютона. Их суть такова: если бросить с высокой горы камень в горизонтальном направлении, то, двигаясь по ветви параболы, он со временем упадёт на Землю. Сообщив ему большую скорость, он упадёт дальше. Поскольку Земля имеет шарообразную форму, то одновременно с продвижением камня по его траектории поверхность Земли удаляется от него. Значит, можно подобрать такое значение скорости камня, при котором поверхность Земли из-за её кривизны будет удаляться от камня ровно на столько, на сколько камень приближается к Земле под действием силы тяжести. Тогда тело будет двигаться на постоянном расстоянии от поверхности Земли, то есть станет её искусственным спутником.
Так как за пределами атмосферы силы сопротивления движению спутнику отсутствуют, то на него будет действовать только сила притяжения к Земле. Поэтому спутник движется как свободно падающее тело с ускорением свободного падения.
Искусственным спутником Земли может стать любое тело произвольной массы. Важно, чтобы ему сообщили за пределами земной атмосферы горизонтальную скорость, при которой оно начнёт двигаться по окружности вокруг Земли.
Скорость, при достижении которой космический аппарат, запускаемый с Земли, может стать её искусственным спутником, называется первой космической скоростью:
По этой же формуле мы можем рассчитать и первую космическую скорость спутника для любой планеты, заменив в ней радиус и массу Земли на радиус и массу исследуемой планеты. Вблизи поверхности Земли первую космическую скорость можно определить, как:
Так, например, наша Луна уже более 4,5 миллиардов лет обращается вокруг Земли. Восемь километров в секунду — это почти 29 000 километров в час! Сообщить телу такую скорость, конечно, не просто. Только в 1957 году советским учёным впервые в истории человечества удалось с помощью мощной ракеты сообщить телу массой около 85 килограмм первую космическую скорость, и оно стало первым искусственным спутником Земли.
Если телу сообщить скорость, большую, чем первая космическая на данной высоте, то орбита спутника будет представлять собой эллипс. И чем больше сообщённая телу скорость, тем более вытянутой будет его орбита.Скорость, при достижении которой космический аппарат, запускаемый с Земли, может преодолеть земное притяжение и осуществить полёт к другим планетам Солнечной системы, называется второй космической скоростью. Расчёты показывают, что для преодоления земного притяжения скорость космического аппарата должна быть больше первой космической скорости в корень из двух раз (без учёта сопротивления воздуха):
В формуле скорость (без индекса) примерно равна 29,8 км/с — это орбитальная скорость нашей планеты. Если в это уравнение подставить все известные величины и произвести вычисления, получим, что тело должно иметь минимальную скорость, примерно равную 16,7 км/с, чтобы начать двигаться по гиперболе и покинуть пределы Солнечной системы.
Конечно же, по записанным нами формулам можно рассчитывать космические скорости не только для Земли, но и других тел Солнечной системы. Для примера давайте определим первую и вторую космические скорости для Луны, если известна её масса и средний радиус.
Как мы уже упоминали, что практически осуществить запуск первого искусственного спутника Земли удалось 4 октября 1957 года, то есть спустя два с половиной столетия после открытия Ньютона. Сейчас же в околоземном пространстве движутся тысячи искусственных спутников Земли, запущенных учёными разных стран. Они обеспечивают непрерывный мониторинг погоды, различных природных явлений, трансляцию телевидения и так далее. А, например, спутниковая навигационная система ГЛОНАСС и другие системы глобального позиционирования позволяют определить координаты любой точки Земли с высокой степенью точностью.
Для полётов космических аппаратов к другим планетам и телам Солнечной системы необходимо производит очень точные расчёты траекторий с использованием законов небесной механики. При их запуске исходят из трёх основных соображений. Во-первых, геоцентрическая скорость космического аппарата при выходе на орбиту относительно Земли должна превышать вторую космическую скорость. Во-вторых, после преодоления притяжения Земли гелиоцентрическая орбита аппарата должна пересекаться с орбитой данной планеты (или другого небесного тела). А также необходимо подобрать такой момент запуска, чтобы орбита аппарата была наиболее оптимальной с точки зрения сроков полёта, затрат топлива и ряда других требований.
Одним из классов межпланетных траекторий являются энергетически оптимальные орбиты, которые соответствуют наименьшей геоцентрической скорости космических аппаратов в момент достижения границы сферы действия Земли.
Рассмотрим одну такую орбиту на примере Марса. Для простоты будем считать, что орбиты Марса и Земли являются круговыми. Для оптимального запуска нужно выбрать такой момент, когда орбитальная скорость Земли и скорость космического аппарата будут сонаправлены. При этом запускаемый аппарат и Марс, двигаясь по своим орбитам, должны одновременно достигнуть точки встречи.
Полученная нами орбита называется полуэллиптической или гомановской, в честь немецкого астронома Вальтера Гомана, занимавшегося теорией межпланетных полётов.
Теперь давайте рассчитаем время полёта Марса по этой полуэллиптической орбите, если его большая полуось равна 1,52 а. е.
Конструкция и оборудование современных космических аппаратов обеспечивают возможность совершения ими весьма сложных манёвров — выход на орбиту спутника планеты, посадка на планету и передвижение по её поверхности и т. п.
Какой скорости достигают космические корабли при межзвездных полетах?
В космосе происходит настоящая гонка существующих на Земле держав. Люди стремятся лучше узнать космос и соревнуются в темпах его покорения. Если говорить про скорость космических кораблей, то гонка будет не абстрактной, а самой настоящей.
На данный момент скорость космических кораблей далека от идеала, но во всем мире ученые и конструкторы работают над ее повышением. Скорость должна быть такой, чтобы преодолеть силу притяжения космического тела и объектов его системы. Данный показатель обладает классификацией:
Чтобы обличить эти показатели в конкретные цифры, применяют коэффициенты отдаления от земного ядра. Но в практике нередко применяют эталонные значения.
На какой скорости можно долететь до Луны?
Сначала потребуется пересилить земное притяжение, нужна скорость 29 тысяч километров в час. Но этого недостаточно, так как понадобится еще и справиться с гравитационным полем самого спутника. Для этого развивают скорость как минимум 40 тысяч км в час. Придерживаясь такого темпа до самой посадки, космический корабль сможет благополучно прилуниться, как это сделали первые люди на Луне. По земным меркам на это уйдет около трех суток, но время в космосе перестает быть постоянной величиной.
Как долететь до Марса и других планет?
Путешествие на Марс займет больше времени, так как находится он значительно дальше. На данном уровне развития технологий на это потребуется более шести месяцев. Самая большая техническая проблема в том, что пилотируемым аппаратам не хватает импульса движения. Объем и масса таких космических кораблей очень большие, и из-за этого они не могут достигнуть нужных величин для стабильного перемещения. Единственная возможность посещения Марса на данный момент — на легких аппаратах, такие используют для сбора образцов. Другие планеты находятся намного дальше, поэтому их посещение на данный момент является несбыточными планами.
Какая скорость максимальная?
Чтобы совершить полет в космос, нужно принять во внимание целый ряд величин. На скорость влияет множество факторов, самый весомый из них — мощность двигателя. Чем большая сила будет создаваться при вырывании газа из сопла, тем мощнее будет продвижение летательного корабля вверх. Интересный факт: чем выше скорость, тем медленнее идет время, это один из удивительных законов космоса.Чтобы определить максимальную скорость для конкретной ракеты, нужно знать не только тип двигателя, но и параметры: вес, размеры, эргономика. Но на данный момент существуют максимальные показатели для аппарата с реактивным двигателем — 10 800-14 400 км в час. Существуют разработки, которые помогут человечеству этот барьер перешагнуть. К такой относят ионный двигатель, с ним летательный аппарат сможет разогнаться до 300 000 км в секунду.
Как нам улететь с Земли: краткое пособие для выезжающих за орбиту
Недавно на хабре появилась новость про планируемую постройку космического лифта. Для многих это показалось чем-то фантастическим и невероятным, вроде огромного кольца из Halo или сферы Дайсона. Но будущее ближе, чем кажется, лестница в небо вполне возможна, и может быть мы даже увидим ее на своем веку.
Сейчас я постараюсь показать, почему мы не можем пойти и купить билет «Земля-Луна» по цене билета «Москва-Питер», как нам поможет лифт и за что он будет держаться, чтобы не рухнуть на землю.
С самого начала развития ракетостроения головной болью инженеров было топливо. Даже в самых современных ракетах топливо занимает где-то 98% массы корабля.
Если нам захочется передать космонавтам на МКС пакетик пряников массой в 1 килограмм, то на это потребуется, грубо говоря, 100 килограмм ракетного топлива. Ракета-носитель одноразовая, и на Землю вернется только в виде обгоревших обломков. Дорогие получаются прянички. Масса корабля ограничена, а значит и полезный груз на один запуск строго лимитирован. И каждый запуск требует расходов.
А если мы хотим полететь куда-то дальше околоземной орбиты?
Инженеры со всего мира сели и стали думать: каким должен быть космический корабль, чтобы увезти на нем больше, и долететь на нем дальше?
Куда долетит ракета?
Пока инженеры думали, их дети нашли где-то селитру и картон и начали мастерить игрушечные ракеты. Такие ракеты не долетали до крыш высотных домов, но дети радовались. Потом самому смышленому пришла мысль: «а давайте натолкаем в ракету больше селитры, и она полетит выше».
Но выше ракета не полетела, так как стала слишком тяжелой. Она даже не смогла подняться в воздух. После некоторого количества экспериментов дети нашли оптимальный объем селитры, при котором ракета летит выше всего. Если добавить больше топлива, масса ракеты тянет ее вниз. Если меньше — топливо заканчивается раньше.
Но как определить, сколько топлива нужно, чтобы ракета не упала в океан с пустым баком, а долетела до Марса?
Вторая космическая скорость
Дети тоже пытались заставить ракету лететь выше. Даже раздобыли учебник по аэродинамике, прочитали про уравнения Навье-Стокса, но ничего не поняли и просто приделали ракете острый нос.
Мимо проходил их знакомый старик Хоттабыч и поинтересовался, о чем грустят ребята.
— Эх, дедушка, если бы у нас была ракета с бесконечным топливом и малой массой, она бы наверное долетела до небоскреба, или даже до самой вершины горы.
— Не беда, Костя-ибн-Эдуард, — ответил Хоттабыч, выдергивая последний волосок, — пусть у этой ракеты топливо никогда не заканчивается.
Радостные дети запустили ракету и стали ждать, когда она вернется на землю. Ракета долетела и до небоскреба, и до вершины горы, но не остановилась и полетела дальше, пока не пропала из вида. Если заглянуть в будущее, то эта ракета покинула землю, вылетела из солнечной системы, нашей галактики и полетела на субсветовой скорости покорять просторы вселенной.
Дети удивились, как это их маленькая ракета смогла так далеко улететь. Ведь в школе говорили, что для того чтобы не упасть обратно на Землю, скорость должна быть не меньше второй космической (11,2 км/с). Разве их маленькая ракета могла развить такую скорость?
Но их родители-инженеры объяснили, что если у ракеты бесконечный запас топлива, то она сможет улететь куда угодно, если сила тяги больше гравитационных сил и сил трения. Так как ракета способна взлететь, силы тяги хватает, а в открытом космосе еще легче.
Вторая космическая скорость — это не скорость, которая должна быть у ракеты. Это скорость, с которой нужно бросить мяч с поверхности земли, чтобы он на нее не вернулся. У ракеты, в отличие от мяча, есть двигатели. Для нее важна не скорость, а суммарный импульс.
Самое сложное для ракеты — преодолеть начальный участок пути. Во-первых, гравитация у поверхности сильнее. Во-вторых, у Земли плотная атмосфера, в которой очень жарко летать на таких скоростях. Да и реактивные ракетные двигатели работают в ней хуже, чем в вакууме. Поэтому летают сейчас на многоступенчатых ракетах: первая ступень быстро расходует свое топливо и отделяется, а облегченный корабль летит на других двигателях.
Константин Циолковский долго думал над этой проблемой, и придумал космический лифт (еще в 1895 году). Над ним тогда, конечно, посмеялись. Впрочем, посмеялись над ним и из-за ракеты, и спутника, и орбитальных станций, и вообще посчитали его не от мира сего: «у нас тут еще автомобили не до конца изобретены, а он в космос собрался».
Потом ученые задумались и прониклись, полетела ракета, запустили спутник, понастроили орбитальных станций, в которые заселили людей. Над Циолковским уже никто не смеется, наоборот, его очень уважают. А когда открыли сверхпрочные графеновые нанотрубки, всерьез задумались и о «лестнице в небо».
Почему спутники не падают вниз?
Все знают про центробежную силу. Если быстро крутить мячик на веревочке, он не падает на землю. Попробуем быстро раскрутить мяч, а затем постепенно замедлим скорость вращения. В какой-то момент он перестанет крутиться и упадет. Это будет минимальная скорость, при которой центробежная сила будет уравновешивать силу притяжения земли. Если крутить мяч быстрее, веревка сильнее натянется (а в какой-то момент лопнет).
Между Землей и спутниками тоже есть «веревка» — гравитация. Но в отличие от обычной веревки она не может натягиваться. Если «крутить» спутник быстрее чем нужно, он «оторвется» (и перейдет на эллиптическую орбиту, или вообще улетит). Чем ближе спутник к поверхности земли, тем быстрее его нужно «крутить». Мяч на короткой веревке тоже крутится быстрее, чем на длинной.
Важно помнить, что орбитальная (линейная) скорость спутника — это не скорость относительно поверхности земли. Если написано, что орбитальная скорость спутника 3.07 км/с, это не значит, что он носится над поверхностью как бешеный. Орбитальная скорость точек на экваторе земли, между прочим, 465 м/с (Земля вертится, как утверждал упрямый Галилей).
На самом деле для мяча на веревочке и для спутника рассчитываются не линейные скорости, а угловые (сколько оборотов в секунду совершает тело). 
Получается, если найти такую орбиту, что угловые скорости спутника и поверхности земли будут совпадать, то спутник будет висеть над одной точкой на поверхности. Такую орбиту нашли, и она называется геостационарная орбита (ГСО). Спутники висят над экватором неподвижно, и людям не приходится поворачивать тарелки и «ловить сигнал».
Бобовый стебель
А что, если спустить с такого спутника веревочку до самой земли, ведь он висит над одной точкой? К другому концу спутника привязать груз, центробежная сила увеличится и будет держать и спутник, и веревочку. Ведь не падает мяч, если его хорошо раскрутить. Тогда можно будет поднимать по этой веревочке грузы прямо на орбиту, и забыть как страшный сон многоступенчатые ракеты, жрущие топливо килотоннами при небольшой грузоподъемности.
Скорость движения в атмосфере у груза будет небольшая, значит нагреваться он не будет, в отличие от ракеты. И энергии на подъем потребуется меньше, так как есть точка опоры.
Главная проблема — масса веревочки. До геостационарной орбиты Земли 35 тысяч километров. Если дотянуть до геостационарной орбиты стальную леску диаметром 1 мм, ее масса будет 212 тонн (а ее нужно тянуть гораздо дальше, чтобы уравновесить лифт центробежной силой). При этом она должна выдерживать свой вес, и вес груза.
К счастью, в этом случае немного помогает то, за что учителя по физике часто ругают учеников: вес и масса — разные вещи. Чем дальше тянется трос от поверхности земли, тем больше он теряет в весе. Хотя удельная прочность троса всё еще должна быть огромной.
С углеродными нанотрубками у инженеров появилась надежда. Сейчас это новая технология, и мы пока не можем свить эти трубочки в длинный трос. И не получается добиться их максимальной расчетной прочности. Но кто знает, что будет дальше?