какая сложность поиска элемента в отсортированном массиве
Алгоритмическая сложность. Алгоритмы поиска. Алгоритмы сортировки.
Для решения одной и той же задачи часто можно придумать более одного алгоритма. В связи с чем, возникает вопрос: какой из алгоритмов “лучше”?
В большинстве случаев, “лучше”, видимо, такой алгоритм, который на тех же входных данных приходит к решению задачи, потребляя меньшее количество вычислительных ресурсов (памяти и времени). Это, конечно, нестрогое рассуждение. Для более строгого рассуждения введем несколько понятий.
Вычислительный процесс алгоритма это последовательность шагов, пройденная при исполнении алгоритма для некоторых входных данных.
Важно понимать разницу между самим алгоритмом и вычислительным процессом, порождаемым этим алгоритмом. Первый является только описанием второго.
Ясно, что время выполнения зависит от конкретного исполнителя. Скажем, электронный калькулятор и суперкомпьютер, вероятно, будут выполнять один и тот же алгоритм разное время.
Однако можно время \(T\) выразить через количество элементарных действий \(k\) и среднее время выполнения элементарного действия \(t\) :
При этом, \(k\) является свойством самого алгоритма, а \(t\) – свойством исполнителя.
Ввиду того, что \(t\) можно считать константой для данного исполнителя, обычно сложность алгоритмов оценивается с точностью до константного множителя. Другими словами, сложность алгоритма оценивается порядком роста.
Кроме времмено́й сложности алгоритма, важной оказывается так же пространственная сложность алгоритма.
\(S\) в общем случае тоже зависит от исполнительного устройства. Скажем, если два исполнительных устройства поддерживают целые длинной 4 и 8 байт соответственно, то пространственная сложность алгоритма на 8-байтных целых будет вдвое больше, чем на 4-байтных целых. Поэтому пространственная сложность оценивается так же порядком роста.
Классы сложности алгоритмов
Выделяются определенные классы сложности: это категории, которые имеют схожую сложность.
Выделяют следующие основные классы сложности:
Кроме того, существуют теоретические классы сложности, которые оперируют понятием недетерменированной машины Тьюринга (НМТ). Их определения совпадают с вышеприведенными, с заменой машины Тьюринга на НМТ, а названия имеют префикс N (например NP), кроме NTIME и NSPACE, где D заменяется на N.
НМТ – это чисто теоретическое построение, которое по принципам действия аналогично МТ, с тем отличием, что для каждого из состояний может быть несколько возможных действий. При этом, НМТ всегда выбирает из возможных действий то, которое приводит к решению за минимально возможное число шагов. Эквивалентно, НМТ производит вычисления всех ветвей и выбирает ту ветвь, которая приводит к решению за минимально возможно число шагов.
Иногда можно услышать, что квантовые компьютеры являются реализацией НМТ. Хотя это может казаться верным в некоторых случаях, в общем случае НМТ является более мощной системой, чем квантовый компьютер.
Известно, что \(P \subseteq NP \subseteq PSPACE \subseteq EXPTIME \subseteq NEXPTIME \subseteq EXPSPACE\)
Вопрос равенства P и NP является одним из главных нерешенных вопросов современной информатики.
Примеры алгоритмов
Приведем несколько примеров простых алгоритмов и рассмотрим их сложность.
Возведение в целую степень
Этот алгоритм был описан в Древней Индии еще до нашей эры и используется для вычисления натуральной степени \(n\) вещественного числа \(x\)
Следует заметить, что существуют более эффективные алгоритмы. Однако по сравнению с “наивной” реализацией, требующей \(\mathcal
Умножение целых
Этот алгоритм умножения называют иногда русским или крестьянским, хотя он был известен еще в Древнем Египте.
Первый множитель последовательно умножается на два, а второй – делится нацело на 2. Результаты записываются в два столбика, пока во втором не получится 1.
Результатом умножения является сумма чисел первого столбика, напротив которых стоят нечетные числа во втором столбике.
Для эффективной реализации алгоритма, дополнительной памяти практически не требуется, и она не зависит от входных данных, поэтому \(S(n) = \mathcal
Опять же, следует заметить, что существуют более эффективные алгоритмы. Однако по сравнению с “наивной” реализацией, требующей \(\mathcal
Пример
Умножение 23 на 43.
Возьмем 23 в качестве второго множителя.
| 43 | 23 | нечетное |
| 86 | 11 | нечетное |
| 172 | 5 | нечетное |
| 344 | 2 | |
| 688 | 1 | нечетное |
Результат \(43+86+172+688 = 989\)
Алгоритмы поиска
Поиск имеет разную сложность если массив упорядочен и если нет. Это связано прежде всего с тем, что об упорядоченном массиве a priori больше информации.
Линейный поиск
Поскольку алгоритм проходит в худшем случае весь массив, сложность \(\mathcal O(n)\) операций сравнения.
Поиск минимального элемента
Имеется массив \(a\) размера \(n\) (индексация с 1), требуется найти минимальный элемент.
Сложность алгоритма \(\mathcal O(n)\)
Бинарный поиск в упорядоченном массиве
В случае если массив упорядочен (скажем, по возрастанию), линейный поиск неэффективен: действительно, сравнив “средний” элемент массива мы можем сразу отсечь половину значений.
Имеется упорядоченный по возрастанию массив \(a\) размера \(n\) (индексация с 1), найти индекс элемента равного \(P\)
Алгоритмы сортировки
Простые сортировки
Сортировка “пузырьком”
Оптимизация: раннее завершение если массив не отсортирован
Сложность: в лучшем случае \(n-1\) операций сравнения (если массив отсортирован). В худшем случае \(n-1+n-2+n-3+\ldots = n(n-1)/2 = \mathcal O(n^2).\) Максимально \(n(n-1)/2 = \mathcal O(n^2).\) обменов.
Сортировка выбором
Сложность: \(n(n-1)/2 = \mathcal O(n^2)\) операций сравнения. Не более \(n-1 = \mathcal O(n)\) обменов.
Сортировка вставками
Сортировка вставками сортирует массив с начала. На каждой итерации алгоритм ищет подходящее место для вставки следующего элемента в уже отсортированную часть.
Сортировка слиянием
Используется метод “разделяй и властвуй”: массив разбивается пополам, каждая из частей рекурсивно сортируется, затем отсортированные части объединяются.
Рекурсия очевидно имеет конечную глубину, т.к. массив 1 элемента тривиально отсортирован.
\[t(n) = 2t(n/2)+c\cdot n\] \[t(1) = \mathcal O(1) = c\]
\[t(n) = 2(2t(n/2^2)+c\cdot n/2)+c\cdot n = 2^2 t(n/2^2)+2c\cdot n\] \[t(n) = 2^2 (2t(n/2^3)+c\cdot n/4)+2c\cdot n = 2^3t(n/2^3)+3c\cdot n\] \[\ldots\] \[t(n) = c 2^ <\log_2 n>+ c\cdot n \log_2 n = c n + c\cdot n\log_2 n = \mathcal O(n\log n)\]
Можно показать (сделаем это позже), что сортировка, основанная на бинарном сравнении, не может иметь сложность ниже \(\mathcal O(n\log n).\)
Сортировка подсчётом
Да, но для этого нужно за каждый шаг алгоритма получать больше информации, чем даёт сравнение.
Простейший вариант сортировки, не использующей напрямую операцию сравнения является сортировка подсчётом.
Рассмотрим некоторый массив целых чисел \(\brace
Построим на основе массива \(\brace
Сложность построения \(\brace
Тогда сложность всего алгоритма – \(\mathcal O(N+\overline x),\) или \(\mathcal O(N)\) если \(\overline x\) – константа.
Этот алгоритм, понятно, применим только если \(\overline x\) сравнительно мало. Действительно, пространственная сложность алгоритма \(\mathcal O(\overline x),\) и, скажем, при \(\overline x = 2^<64>,\) потребуется по меньшей мере 18 эксабайт (18·10¹⁸ байт, 18 млн терабайт) дополнительной памяти.
Поразрядная сортировка (radix sort)
Отметим также что алгоритм требует \(\mathcal O(N+P)\) дополнительной памяти.
Сложность двоичного поиска в отсортированном массиве
Вы будете перенаправлены на Автор24
Двоичный поиск в отсортированном массиве — это стандартный алгоритм поиска компонентов в отсортированном массиве, который применяет деление массива пополам.
Алгоритм двоичного поиска имеет следующие синонимы: бинарный поиск, способ половинного деления, дихотомия.
Общая структура алгоритма
Способ двоичного поиска применяется как быстрая версия поискового алгоритма в предварительно прошедшем сортировку массиве. Он приобрёл широкую популярность, поскольку обладает самой маленькой высотой алгоритма из всех допустимых и некоторыми достоинствами его вычислительных параметров. И кроме того, если брать не числовые алгоритмы, он обладает свойством рекурсивности, то есть его легко записать. Базовой чертой алгоритма является дробление массива на равные половинки и затем, выполнении рекурсивного поиска в одной из половин. Ниже приведён пример поиска элемента «четыре» в массиве:
Рисунок 1. Поиск элемента «четыре» в массиве. Автор24 — интернет-биржа студенческих работ
Впервые этот способ был упомянут на занятиях в школе Мура Джона Мокли в середине пятидесятых годов прошлого века. Сначала алгоритм предназначался лишь для массивов длины:
но в конце пятидесятых годов прошлого века Д.Г.Лемер разработал методику, которая позволяла работать с массивами любых размеров. Позднее Герман Боттенбрух реализовал этот алгоритм на языке Алгол, где сравнение выполнялось в конце и увеличивало число итераций алгоритма на единицу, но при этом уменьшало количество операций сравнения до одного на каждую итерацию. Конкурентом данного способа считается метод линейного поиска, что означает полный перебор вариантов. Он обладает следующей сложностью вычислений:
Готовые работы на аналогичную тему
но способен работать на массивах, которые были упорядочены в произвольном порядке. Сравнение особенностей использования этих методик показывает, что метод линейного поиска имеет преимущества при:
Двоичный поиск предполагает предварительную сортировку со сложностью, определяемую выражением:
Бинарный поиск удобен при больших размерах массивов и многократном его повторении. История формирования и развития методики двоичного поиска, следующая. В 1971-ом году А.К. Чандра представил методику однородного двоичного поиска Дональду Кнуту, опубликовавшему этот метод в своей научной работе.
Затем появился метод троичного поиска, при котором выполнялось деление отрезка на три участка. Он используется для определения местоположения функционального экстремума.
Метод интерполирующего поиска, при котором участок поиска не делился на два, а выполнялось предсказание позиции компонента поиска на базе разницы значений. Данный метод обладает большим быстродействием, при достаточно равномерном распределении элементов. Средняя сложность задаётся выражением:
Но при самом плохом раскладе, сложность будет равна:
В 1986-ом году Бернар Шазеллем и Леонидас Дж. Губайс предложили вариант, который назвали дробный спуск, и который ускорил двоичный поиск в многомерных массивах.
Близким вариантом к двоичному поиску в массиве является способ бисекции или способ половинного деления. Его основным отличием считается вычисление величины функции вместо определения компонента массива согласно его индексации, и, кроме того, применение действительных чисел как аргументов, являющихся индексами компонентов массива. По своим свойствам, алгоритм может определяться как в рекурсивной, так и в итеративной форме. Ядро для вычислений в обеих формах одно и тоже, но при рекурсии имеется добавочная нагрузка, которая состоит в вызове функций и сохранении их стека.
Математическое представление алгоритма
В качестве исходных данных возьмём одномерный массив nn чисел
в котором выполнено упорядочивание по не убыванию или же по не возрастанию. Кроме того, имеем число АА, которое требуется отыскать в данном массиве. Данные, подлежащие вычислению, это индексный номер компонента, который равняется требуемому. Или же отрицательный ответ при отсутствии такого компонента. Формулировка методики следующая. Компоненты на всех этапах алгоритма представляются как непрерывный отрезок массива. Каждая пара содержит сумму компонентов, которые её составляют. На очередном шаге на пары делятся уже данные суммы, а также компоненты, не вошедшие в уже известные суммы, и так далее. На каждом шаге итерации выполняется одно действие, а именно вычисляется среднее арифметическое левого и правого индексов:
mk = lk + rk2mk = lk + rk2
Где символами lk, rk, mklk, rk, mk обозначена индексация левого и правого окончания, а также середины данного отрезка массива при кк-ом шаге итерации.
Первоначально выполняется поиск по всем элементам массива, поэтому
l0 = 0, r0 = n−1l0=0, r0=n−1
Ядром вычислений способа двоичного поиска являются операции сравнения и определения середины отрезка, выполняемые рекуррентно для постоянно уменьшающегося в размерах массива. Общее число операций сложения, умножения и сравнения прямо пропорционально числу шагов итерации, а оно не может быть более, чем:
Само определение алгоритма подразумевает наличие в нём рекурсивных вызовов одного и того же действия для постоянно уменьшающихся массивов. При это не применяются никакие стандартные макрооперации.
Выполнение последовательного алгоритма можно разбить на следующие этапы:
Этап 1. Выполнение инициализации концов отрезка с помощью концов массива:
l0 = 0, r0 = n−1l0 = 0, r0 = n−1
Этап 2. В случае, когда lk\gtrklk\gtrk, то это означает завершение поиска как неуспешного. В противном случае ищется позиция середины отрезка массива как целая часть от половины суммы позиций его окончаний:
mk = [lk + rk2]mk = [lk + rk2].
Этап 3. В случае, когда xmk\ltAxmk\ltA, тогда определяем:
lk:=mk+1lk:=mk+1 и возвращаемся ко второму этапу.
Этап 4. В случае, когда xmk = Axmk = A, поиск завершается ввиду отсутствия искомого значения и возвращается номер позиции mkmk.
Оцениваем сложность алгоритмов: что такое О(log n)?
Если вы сталкивались с алгоритмами, то наверняка видели обозначения типа O(log n), а также слышали о логарифмической вычислительной сложности. Давайте освежим в памяти, что это такое, и как оценивается сложность алгоритмов.
Итак, обычно сложность алгоритмов оценивают по времени выполнения либо по используемой памяти. Как бы там ни было, сложность будет зависеть от размеров входных данных. Очевидно, что массив из ста элементов обработается быстрее, чем из тысячи. При этом здесь нас мало интересует точное время, ведь оно зависит от типа данных, процессора, языка программирования и прочих параметров. Главное — это асимптотическая сложность — сложность при стремлении размера входных данных к бесконечности.
Представьте, что какому-то алгоритму надо выполнить 4n 3 + 7n условных операций для обработки n элементов входных данных. Если увеличивать n, на итоговое время работы будет намного сильнее влиять возведение n в куб, а не умножение n на 4 либо прибавление 7n. А значит, можно сказать, что временная сложность такого алгоритма равна О(n 3 ) и она кубически зависит от размера входных данных.
Что касается заглавной О (О-нотация), то это пришло из математики, т. к. данную букву используют, чтобы сравнивать асимптотическое поведение функций. Формально O(f(n)) будет значить, что объём занимаемой памяти либо время работы алгоритма растёт в зависимости от объёма входных данных, что происходит не быстрее, чем константа, умноженная на f(n).
Линейная сложность — O(n)
Линейной сложностью обладает, к примеру, алгоритм поиска наибольшего элемента в несортированном массиве. Чтобы понять, какой элемент массива максимальный, нам понадобится пройтись по всем n-элементам этого массива.
Логарифмическая сложность — O(log n)
Тут можно вспомнить бинарный поиск. Когда массив отсортирован, можно его проверить на наличие конкретного значения по методу деления пополам. Если при проверке среднего элемента мы увидим, что он больше искомого, мы отбросим вторую половину массива. Если меньше, отбросим первую половину. И так до тех пор, пока не проверим log n элементов.
Квадратичная сложность — O(n 2 )
Есть и другие оценки по сложности, но основаны они на том же принципе.
Также бывает, что время работы алгоритма не зависит от размера входных данных. В этом случае сложность обозначается как O(1). К примеру, чтобы определить значение третьего элемента массива не надо ни запоминать элементы массива, ни проходить по ним некоторое число раз. Здесь надо дождаться в потоке входных данных 3-й элемент, что и будет итогом, на вычисление которого для любого объёма данных потребуется одно и то же время. Схожим образом проводят оценку по памяти.
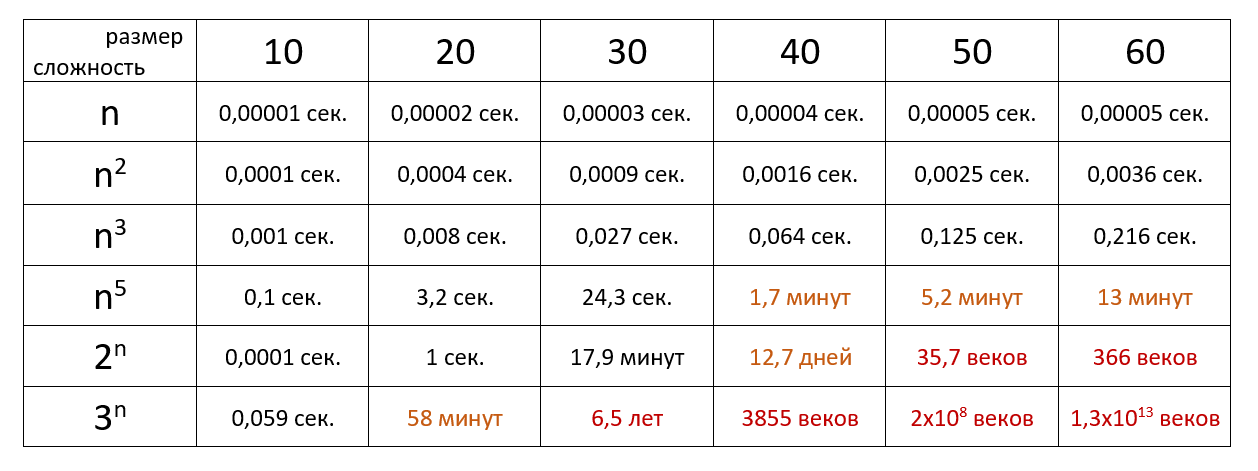
Наглядный пример
Теперь давайте посмотрим на время выполнения алгоритма определённой сложности с учётом размера входных данных и при скорости 10 6 операций в секунду:
Вот и всё! Если же хотите разбираться в алгоритмах на уровне разработчика, вам сюда.
Arrays, Collections: Алгоритмический минимум
Массивы и списки
Недавно на собеседовании в крупную компанию на должность Java разработчика меня попросили реализовать стандартный алгоритм сортировки. Поскольку я никогда не реализовывал самописные алгоритмы сортировки, а пользовался всегда готовыми решениями, у меня возникли затруднения с реализацией. После собеседования я решил разобраться в вопросе и подготовить список основных алгоритмов сортировки и поиска, которые используются в стандартном пакете java — Java Collections Framework (JCF). Для этого я изучил исходники Oracle JDK 7.80 (UPD: добавлена ссылка).
В самом обобщенном виде результат изучения представлен на рисунке. Подробности — в основном тексте.
Рисунок 1. Методы Arrays, Collections и реализуемые ими алгоритмы
Первое, что поразило меня в алгоритмах, реализованных в Arrays и Collections — то, что их можно буквально по пальцам пересчитать — по большому счету, это два алгоритма сортировки и один алгоритм поиска.
Второе — то, что сортировка списков «под капотом» использует сортировку массивов.
Третье — то, что один из алгоритмов сортировки портирован с python.
Алгоритм быстрой сортировки с двумя опорными элементами разработан нашим соотечественником Владимиром Ярославским и реализован при содействии Джона Бентли и Джошуа Блоха.
Алгоритм сортировки слиянием, который является основным для сортировки массивов ссылочных типов, буквально назван по имени своего создателя Tim Peters — TimSort. Этот алгоритм был адаптирован Джошуа Блохом с алгоритма сортировки списков, реализованном на python Тимом Петерсом.
Кратко излагая результаты, стоит отметить, что:
Итак, для того, чтобы выяснить, какие основные и дополнительные алгоритмы используются в пакете util, нужно разобрать реализацию 4-х методов из API Collections и API Arrays.
Таблица 1. API Arrays vs API Collections
| Метод | Arrays API | Collections API |
|---|---|---|
| Sort method | Arrays.sort | Collections.sort |
| Search method | Arrays.binarySearch | Collections.binarySearch |
Arrays.sort
Массивы примитивных типов
Основной алгоритм сортировки для массивов примитивных типов в Arrays — быстрая сортировка. Для реализации этой сортировки выделен финальный класс DualPivotQuickSort, который предоставляет публичные методы sort для сортировки массивов всех примитивных типов данных. Методы Arrays API вызывают эти методы и пробрасывают в них ссылку на массив. Если требуется отсортировать определенный диапазон массива, то передаются еще и индексы начала и конца диапазона.
Временная сложность алгоритма быстрой сортировки в лучшем случае и в среднем случае составляет O(n log n). В некоторых случаях (например, на малых массивах) алгоритм быстрой сортировки обладает не лучшей производительностью, деградирует до квадратичной сложности. Поэтому имеет смысл вместо него применять другие алгоритмы, которые в общем случае проигрывают, но в конкретных случаях могут дать выигрыш. В качестве дополнительных алгоритмов были выбраны сортировка вставками, “обычная” быстрая сортировка (с одной опорной точкой), сортировка подсчетом.
Инженеры Oracle эмпирическим путем вычислили оптимальные размерности массивов для задействования каждого дополнительного алгоритма сортировки. Эти значения записаны в приватных полях класса DualPivotQuickSort. Для наглядности я свел их в таблицу 2.
Я не могу написать бинарный поиск
Недавно (буквально два года назад) тут пробегала статья Только 10% программистов способны написать двоичный поиск. Двоичный поиск — это классический алгоритм поиска. Мало того, это еще чрезвычайно простой алгоритм, который можно очень легко описать: берем отсортированный массив, смотрим в середину, если не нашли там число, в зависимости от того, что в середине — ищем это число этим же методом либо в левой части, либо в правой, откидывая средний элемент. Для функций также, просто берем не массив, а функцию. Все очень и очень просто, алгоритм описан почти везде, все баги словлены и описаны.
Так вот, я не могу реализовать двоичный поиск. Для меня он ни капельки не тривиален. Наверное, я ненастоящий программист. А ведь так и есть, я всего-лишь студент, но ведь это не оправдание? Если точнее, я не могу реализовать хороший корректный красивый двоичный поиск. Все время у меня вылезает проблема либо с корректностью, либо с красивостью, либо и с тем, и с другим. Так что, да, заголовок немного желтоват.
Прежде чем читать этот топик, напишите свою версию бинарного поиска — для отсортированного массива. Причем, в зависимости от параметра, поиск должен выдавать или первый элемент, или любой из дублирующих. Еще для сравнения, напишите бинарный поиск для функций
Для начала, я буду писать код на C#. Я надеюсь, поклонники других языков с легкостью поймут мой код. Границы поиска я буду представлять в виде полуинтервала [left; right), т.е. точка left включается, а точка right выключается. Для меня полуинтервалы удобнее, к их поведению я уже привык, кроме того, использование полуинтервалов имеет некоторые преимущества при программировании различных алгоритмов (о чем мы поговорим позже). Вообще, использовать полуинтервалы более правильно с точки зрения поддержки «единого стиля программирования», так как я пишу циклы вот так:а не так:
Я буду писать одновременно рекурсивную и итеративную версию, но мне ближе рекурсивная, так что не обессудьте. Для рекурсивной версии мы сделаем вот такую вот красивую обертку:
Первая попытка
Кстати, теперь можно добавить еще одну причину к использованию полуинтервалов: если у нас есть интервал [left, right], то мы должны его разбить на [left, mid — 1] и [mid + 1; right] (что конечно, чуть проще для запоминания, но весьма странно).
У полуинтервалов различие в индексах равно 1 (одному элементу, который мы выбрасываем), а у интервалов — 2 — магической цифре, взятой с потолка.
Особенно это заметно для сортировки слиянием, где для полуинтервалов различия в индексах нету (массив делится на [left, mid) и [mid, right)), а для интервалов появляется различие равное 1 (так как массив делится на [left, mid] и [mid + 1, right], или [left, mid — 1] и [mid, right]).
Теперь, осталось определить, в какой части массива нужно искать элемент, в зависимости от того, меньше ли средний элемент (array[mid]), чем ключ (key). Сделать это весьма просто — нужно просто подставить сначала один знак, проверить, работает ли программа, а если не работает, то другой :-). Почему-то именно такой способ проверки я и использую. Мне постоянно кажется, что перекомпилировать быстрее, чем «подумать».
Рекурсивно:
Итеративно:
Разбор полетов:
Если внимательно вчитаться в итеративную версию программы, то сразу становится понятно, что если элемента нет, то алгоритм никогда не остановится. Пониманию этого факта очень способствует while(true), которого в рекурсивной версии программы, естественно нет. И хотя я написал кучу реализаций рекурсивных алгоритмов, я все еще иногда сталкиваюсь с тем, что забываю остановить рекурсию. Как можно написать итеративную версию с подвохом, я не знаю.
Вторая попытка
Кстати, останавливать рекурсию мы будем в случае left == right, т.е., когда интервал стал таким — [left, right). Ну или в случае, когда right — left key
Т.е. если флаг descendingOrder не установлен, то выбор идет как обычно, если установлен, то выбор идет наоборот. Но это «хак», и возможно, что нужно написать какой-нибудь комментарий. Я не знаю, что именно он должен содержать.
Рекурсивно:
Итеративно:
Разбор полетов:
На всякий случай: один из вариантов проверки направления сортировки не учитывал, что массив может быть пуст. Я решил не выделять этот фейл в отдельную попытку.
Попытка №4
Дабы мы не попали на еще одну попытку, сразу скажу, что теперь рекурсию нужно останавливать еще и в случае, когда самый первый элемент из полуинтервала равен ключу. Ну а в случае, когда мы узнали, что средний элемент равен ключу у нас есть два варианта. Либо средний следует за первым и нужно выдавать именно его, ибо первый не равен ключу, поскольку рекурсия еще не остановилась. Либо нужно укорачивать область поиска (см. картинку выше)