Активное, реактивное и полное сопротивление цепи

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением.

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление, обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Активное сопротивление определяет действительную часть импеданса:

, где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии(в тепловую энергию)

Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

– величина полного реактивного сопротивления

Индуктивное сопротивление ( ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.

Ёмкостное [1] сопротивление ( ).

Здесь — циклическая частота

Полное сопротивление цепи при переменном токе:

Билет №12.

При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.

При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.

Источник

Активное и реактивное сопротивление, треугольник сопротивлений

Активное и реактивное сопротивления

Если какой-либо проводник включить в цепь переменного тока, то окажется, что его сопротивление будет несколько больше, чем в цепи постоянного тока. Это объясняется явлением, получившим название скин-эффекта (поверхностный эффект).

Это объясняется тем, что точки, лежащие ближе к центру, пересекаются большим числом силовых линий. Под действием этой ЭДС переменный ток будет распределяться не по всему сечению проводника равномерно, а ближе к его поверхности.

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление — физическая величина, характеризующая сопротивление электрической цепи (или её участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы (преимущественно в тепловую). Выражается в омах.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

Известно, что если постоянный ток, проходящий по какой-либо обмотке, прерывать и замыкать, то одновременно с изменением тока будет изменяться и магнитный поток внутри обмотки, в результате чего в ней возникнет ЭДС самоиндукции.

То же самое будет наблюдаться и в обмотке, включенной в цепь переменного тока, с той лишь разницей, что здесь ток непрерывно изменяется как по величине, так и по направлению. Следовательно, непрерывно будет изменяться величина магнитного потока, пронизывающего обмотку, и в ней будет индуктироваться ЭДС самоиндукции.

Но направление ЭДС самоиндукции всегда таково, что противодействует изменению тока. Так, при возрастании тока в обмотке ЭДС самоиндукции будет стремиться задержать нарастание тока, а при убывании тока, наоборот, будет стремиться поддержать исчезающий ток.

Отсюда следует, что ЭДС самоиндукции, возникающая в обмотке (проводнике), включенной в цепь переменного тока, будет всегда действовать против тока, задерживая его изменения. Иначе говоря, ЭДС самоиндукции можно рассматривать как дополнительное сопротивление, оказывающее вместе с активным сопротивлением обмотки противодействие проходящему через обмотку переменному току.

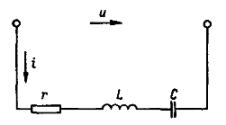
Рис. 1. Цепь переменного тока с резистором, катушкой индуктивности и конденсатором.

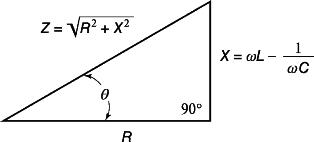
Графически это выражение можно изобразить в виде, так называемого, треугольника сопротивлений.

Рис.2. Треугольник сопротивлений

Гипотенуза треугольника сопротивлений изображает полное сопротивление цепи, катеты — активное и реактивное сопротивления.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Какая связь между полным активным и реактивным сопротивлениями цепи переменного тока

При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.

Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.

Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.

Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки

Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.

Сопротивление конденсатора можно рассчитать по формуле

Источник

Полное сопротивление цепи переменного тока

В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U_L (напряжение на индуктивном сопротивлении) и напряжения U_R (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов U_L и U_R. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор U_AB является гипотенузой прямоугольного треугольника.

Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

(1)

Извлекая квадратный корень из обеих частей этого равенства, получим,

(2)

Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного случая:

(3)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

(4)

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X_L или X_C преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)

(6)

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

(7)

Приводя к общему знаменателю подкоренное выражение, получим:

(8)

(9)

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

(10)

Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.

В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.

Формула полного сопротивления для этого случая будет:

(11)

Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)

В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

(13)

При соблюдении этого условия полное сопротивление колебательного контура будет равно:

(14)

где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Какая связь между полным,активным и реактивным сопротивлениями цепи переменного тока

При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.

Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.

Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.

Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки

Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.

Сопротивление конденсатора можно рассчитать по формуле

Источник