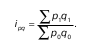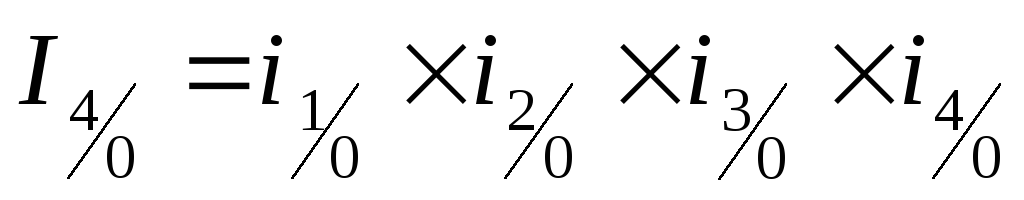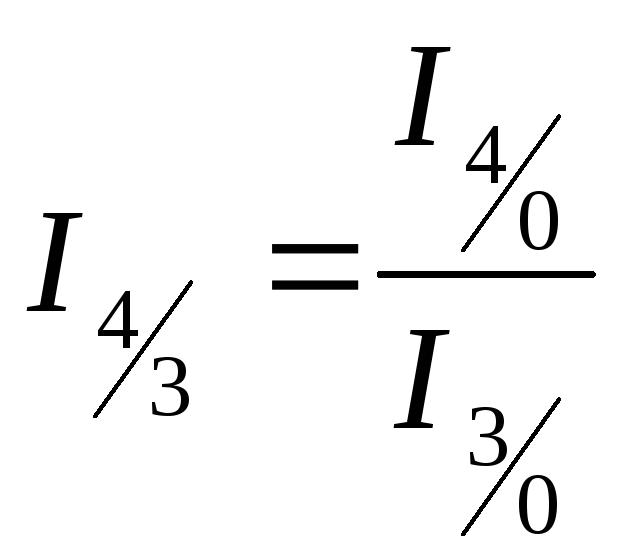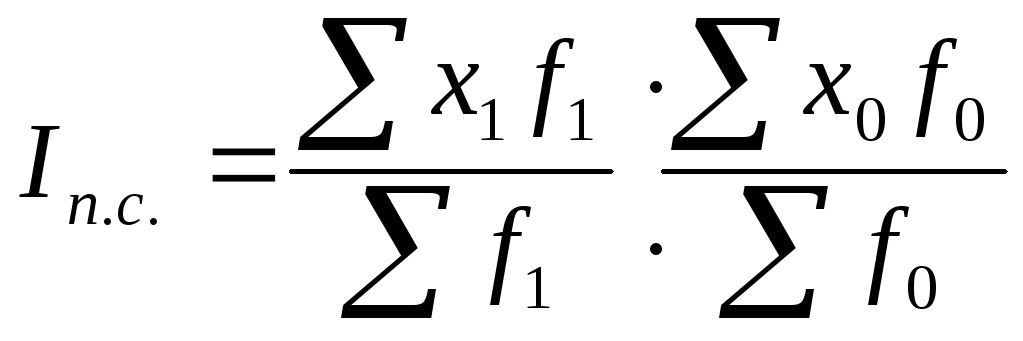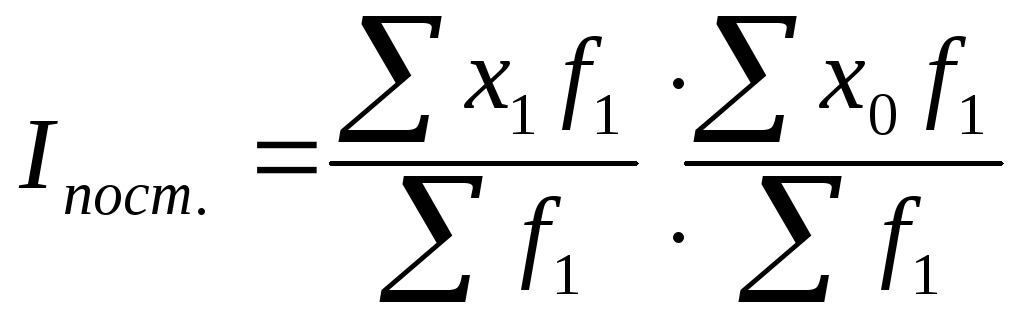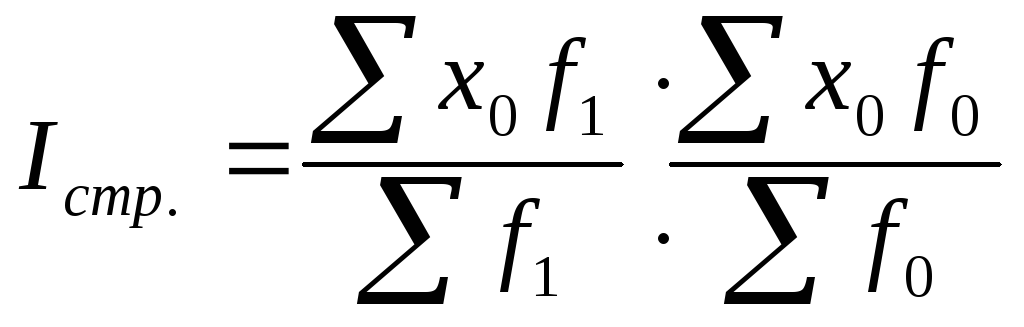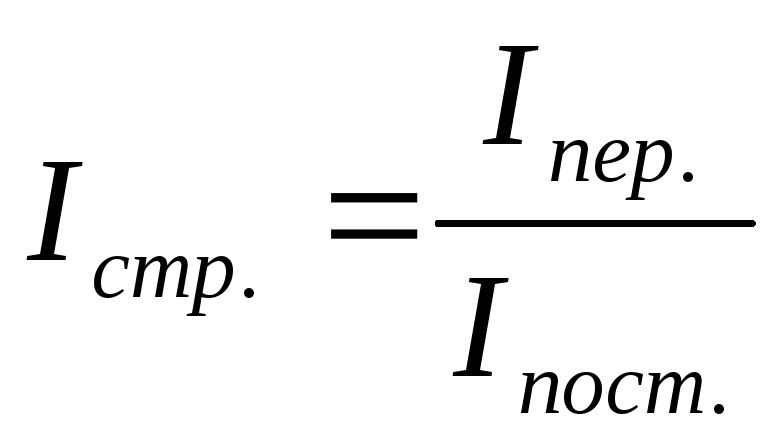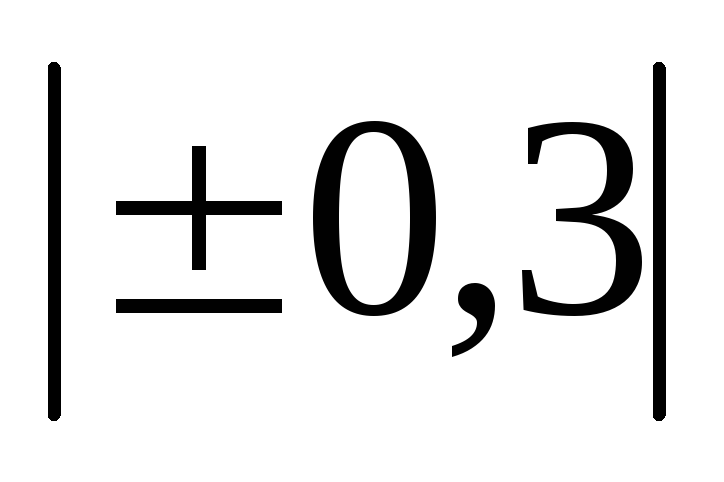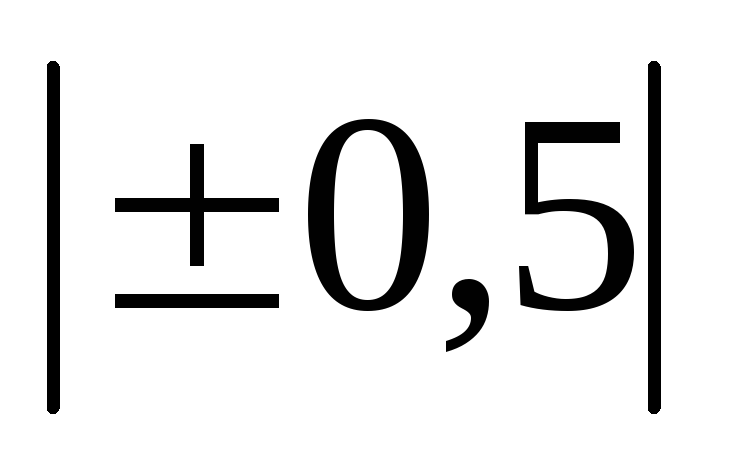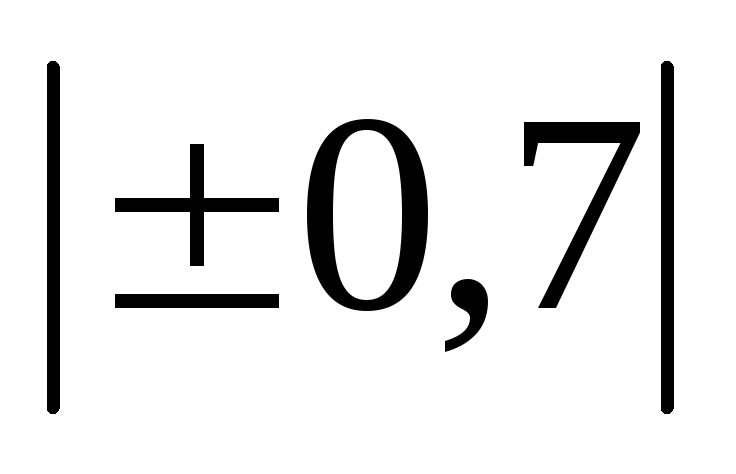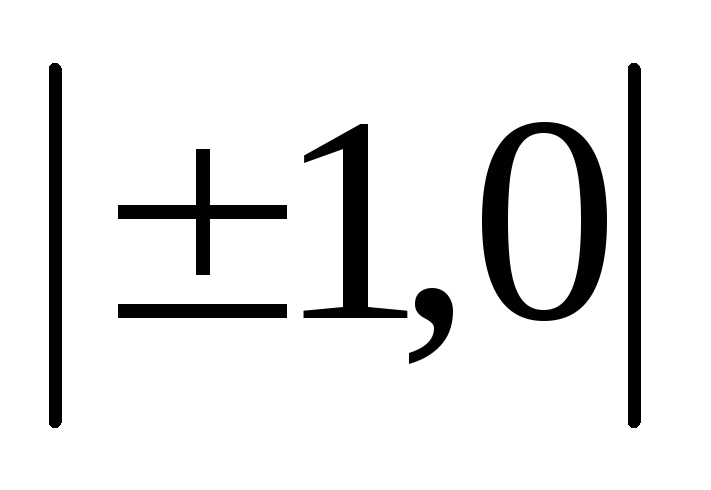какая взаимосвязь существует между базисными и цепными индексами
Индивидуальные базисные и цепные индексы. Общие индексы
Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.
Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой – базисные, а во втором – индексы с переменной базой – цепные.
В экономическом анализе базисные и цепные индексы обладают определенными значениями.
Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.
Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному. Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве соизмерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.
Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.
Формула общего индекса товарооборота:
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.
Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических индексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.
Расчет агрегатного индекса цен был предложен немецким экономистом Г. Пааше.
Какая взаимосвязь существует между базисными и цепными индексами
8.5 гЕРОЩЕ Й ВБЪЙУОЩЕ ЙОДЕЛУЩ. йОДЕЛУЩ У РПУФПСООЩНЙ Й РЕТЕНЕООЩНЙ ЧЕУБНЙ
йОДЕЛУЩ НПЗХФ ЙУРПМШЪПЧБФШУС ДМС БОБМЙЪБ ДЙОБНЙЛЙ УПГЙБМШОП-ЬЛПОПНЙЮЕУЛЙИ СЧМЕОЙК ЪБ ОЕЛПФПТЩК ЙОФЕТЧБМ ЧТЕНЕОЙ, ЧЛМАЮБАЭЙК ВПМЕЕ ДЧХИ РЕТЙПДПЧ. ч ЬФПН УМХЮБЕ ТБУУЮЙФЩЧБАФУС УЙУФЕНЩ ЙОДЕЛУПЧ.
ч ЪБЧЙУЙНПУФЙ ПФ ВБЪЩ УТБЧОЕОЙС УЙУФЕНЩ ЙОДЕЛУПЧ ВЩЧБАФ ГЕРОЩНЙ Й ВБЪЙУОЩНЙ.
ьФЙ УЙУФЕНЩ ЙОДЕЛУПЧ НПЗХФ ВЩФШ РПУФТПЕОЩ ДМС ЙОДЙЧЙДХБМШОЩИ Й ПВЭЙИ ЙОДЕЛУПЧ.
уЙУФЕНЩ ЙОДЙЧЙДХБМШОЩИ ЙОДЕЛУПЧ УФПЙНПУФЙ РТПДХЛГЙЙ, ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ Й ГЕО РТЕДУФБЧМЕОЩ Ч ФБВМЙГЕ 8.5.
оБЪЧБОЙЕ ЙОДЙЧЙДХБМШОПЗП ЙОДЕЛУБ
йОДЕЛУ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ
бОБМПЗЙЮОП ЬФЙН УЙУФЕНБН ЙОДЕЛУПЧ УФТПСФУС УЙУФЕНЩ ЙОДЙЧЙДХБМШОЩИ ЙОДЕЛУПЧ Й ДМС ДТХЗЙИ РПЛБЪБФЕМЕК.
рТЙ РПУФТПЕОЙЙ УЙУФЕН ПВЭЙИ ЙОДЕЛУПЧ ЙУРПМШЪХАФУС РПУФПСООЩЕ Й РЕТЕНЕООЩЕ ЧЕУБ.
уЙУФЕНПК ЙОДЕЛУПЧ У РПУФПСООЩНЙ ЧЕУБНЙ ОБЪЩЧБЕФУС УЙУФЕНБ УЧПДОЩИ ЙОДЕЛУПЧ ПДОПЗП Й ФПЗП ЦЕ СЧМЕОЙС, ЧЩЮЙУМЕООЩИ У ЧЕУБНЙ, ОЕ НЕОСАЭЙНЙУС РТЙ РЕТЕИПДЕ ПДОПЗП ЙОДЕЛУБ Л ДТХЗПНХ.
оБРТЙНЕТ, УЙУФЕНБ ВБЪЙУОЩИ ЙОДЕЛУПЧ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ У РПУФПСООЩНЙ ЧЕУБНЙ (p 0 ) ЙНЕЕФ ЧЙД:
уЙУФЕНХ ГЕРОЩИ ЙОДЕЛУПЧ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ У РПУФПСООЩНЙ ЧЕУБНЙ (p 0 ) НПЦОП РТЕДУФБЧЙФШ УМЕДХАЭЙН ПВТБЪПН:
оБРТЙНЕТ, УЙУФЕНБ ВБЪЙУОЩИ ЙОДЕЛУПЧ ГЕО У РЕТЕНЕООЩНЙ ЧЕУБНЙ ЙНЕЕФ УМЕДХАЭЙК ЧЙД:

Б УЙУФЕНБ ГЕРОЩИ ЙОДЕЛУПЧ ГЕО У РЕТЕНЕООЩНЙ ЧЕУБНЙ:
уЙУФЕНЩ ПВЭЙИ ЙОДЕЛУПЧ ДТХЗЙИ РПЛБЪБФЕМЕК УФТПСФУС БОБМПЗЙЮОП. нЕЦДХ ГЕРОЩНЙ Й ВБЪЙУОЩНЙ ЙОДЕЛУБНЙ УХЭЕУФЧХАФ ТБЪМЙЮОЩЕ ЧЙДЩ УЧСЪЙ:
1. еУМЙ ЙЪЧЕУФОЩ ГЕРОЩЕ ЙОДЕЛУЩ, ФП РПУМЕДПЧБФЕМШОП РЕТЕНОПЦЙЧ ЙИ НПЦОП РПМХЮЙФШ ВБЪЙУОЩЕ ЙОДЕЛУЩ.
2. ъОБС РПУМЕДПЧБФЕМШОЩЕ ЪОБЮЕОЙС ВБЪЙУОЩИ ЙОДЕЛУПЧ, НПЦОП ТБУУЮЙФБФШ Б ЙИ ПУОПЧЕ ГЕРОЩЕ ЙОДЕЛУЩ.
Цепные и базисные индексы



Для более глубокого изучения динамики экономических процессов, выявления закономерностей и тенденций их развития недостаточно рассчитать индекс только за отчетный год, для этого проводятся сопоставления индексов за ряд последовательных периодов. В этом случае следует различать цепные и базисные индексы.
Цепные индексы – это система индексов в ряду динамики, рассчитанных последовательно как отношение текущего уровня ряда к предыдущему уровню ряда. Индексируемая величина каждый раз меняется и представляет собой каждый следующий период. Базисная величина также меняется и представляет собой величину, непосредственно стоящую перед индексируемой величиной.
Базисные индексы – это система индексов в ряду динамики, рассчитанных последовательно как отношение каждого последующего уровня к одной и той же базисной величине. В качестве базисной величины обычно применяется начальный уровень динамического ряда.
Цепные индексы применяются для оценки скорости изменения изучаемого явления от периода к периоду. Базисные же индексы применяются для оценки степени изменения явления за большой промежуток времени, включающий в себя несколько отчетных периодов.
Система цепных и базисных индексов может быть исчислена как для отдельного элемента сложной совокупности – это индивидуальные индексы, так и для всей совокупности – это общие индексы.
Рассчитать цепные и базисные индивидуальные индексы, характеризующие изменение остатков готовой продукции организации на складе.
Таблица 34 – Запасы готовой продукции вида «А» на складе
по состоянию на начало кварталов
| Квартал | Отчетный год | 1 квартал следующего года | |
| 1 кв. | 2 кв. | 3 кв. | 4 кв. |
| Объем запаса на начало квартала, ед. |
1) Рассчитаем цепные индексы динамики:
– 2-ой кв. по отношению к 1-му: 545 / 540 = 1,009 или 100,9%
– 3-ий кв. по отношению ко 2-му: 552 / 545 = 1,013 или 101,3%
– 4-ый кв. по отношению к 3-му: 562 / 552 = 1,018 или 101,8%
– 1-ый кв. сл. года к 4-му кв.: 580 / 562 = 1,032 или 103,2 %
Изучая уровни ряда, мы уже можем отметить негативную тенденцию изменения запасов готовой продукции – они возрастают от квартала к кварталу. Кроме того, цепные индексы показали возрастающую скорость увеличения запасов готовой продукции. Если во втором квартале запас возрос только на 0,9 %, то в первом квартале следующего года – уже на 3,2 %. Это подтверждает негативную тенденцию сокращения рынка сбыта данной продукции.
2) Рассчитаем базисные индексы динамики по отношению к первому кварталу:
– 2-ой кв.: 545 / 540 = 1,009 или 100,9 %
– 3-ий кв.: 552 / 540 = 1,022 или 102,2 %
– 4-ый кв.: 562 / 540 = 1,041 или 104,1 %
– 1-ый кв. сл. года: 580 / 540 = 107,4 %
Базисные индексы также показывают возрастающую скорость увеличения запасов. Если по сравнению с первым кварталом запас возрос во втором квартале только на 0,9 %, то в первом квартале следующего года – уже на 7,4 %. В течение всего года объем запаса накапливался и за весь год возрос на 7,4 %.
Цепные и базисные индивидуальные индексы имеют следующую взаимосвязь:
– последовательное произведение цепных индексов n-периода и всех предыдущих периодов дает базисный индекс n- периода в анализируемом ряду:
– отношение базисного индекса n-периода к предыдущему индексу n-1 периода дает цепной индекс n-периода:
в 3-ем квартале: 1,022 / 1,009 = 1,013 или 101,3 %
в 4-ом квартале: 1,041 / 1,022 = 1,018 или 101,8 %
в 1-ом квартале сл. года: 1,074 / 1,041 =1,032 или 103,2 %.
Аналогичные правила приемлемы и для агрегатных индексов с постоянными весами. Приведем несколько последовательных формул расчета цепных агрегатных индексов физического объема продукции:
Формулы расчета базисных агрегатных индексов физического объема продукции:
Произведение цепных агрегатных индексов дает базисный индекс:
Отношение двух соседних базисных агрегатных индексов дает цепной агрегатный индекс, например:
12.4. Базисные и цепные индексы, их взаимосвязь
Так как индексы являются относительной величиной динамики, то они также могут быть базисными и цепными:
– базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения, т.е. база сравнения, остаётся постоянной;
– цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
Для индивидуальных индексов цен, физического объёма и стоимости продукции справедливо следующее правило:
1. Последовательное произведение цепных индексов даёт базисный индекс последнего периода:
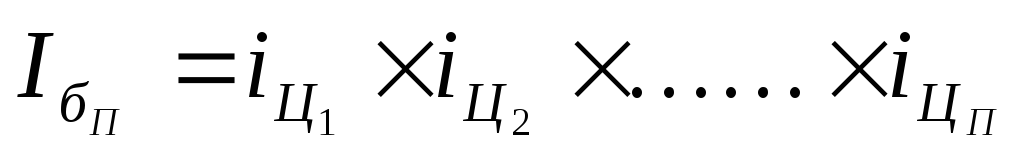
2. Отношение базисного индекса отчётного периода к базисному индексу предшествующего периода даёт цепной индекс отчётного периода
и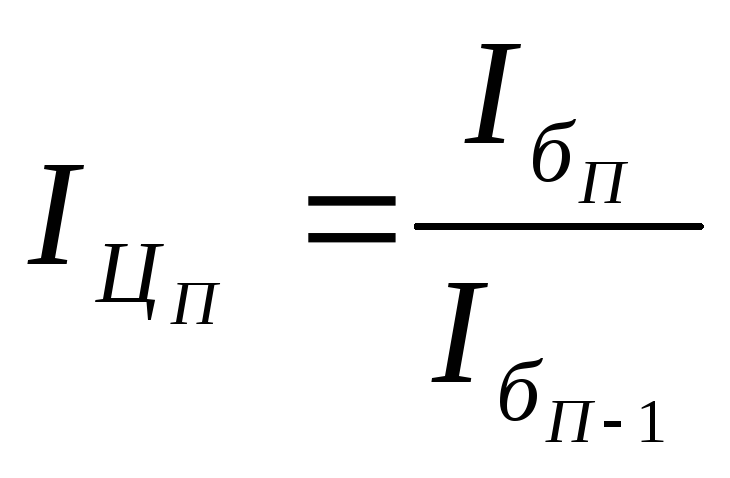
Имеются следующие данные об изменении численности рабочих на заводе, в % к предыдущему году:
Определить на сколько процентов увеличилось число рабочих на заводе за 5 лет, т.е. в 2011 году по сравнению с 2006 годом.
Зная, что базисный индекс можно получить путем перемножения цепных индексов, находим:
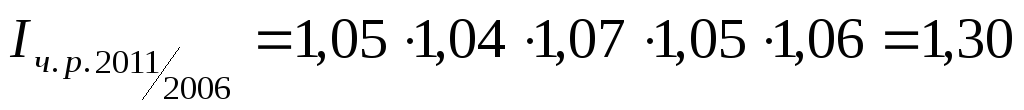
12.5. Индексы средних величин
2. Индекс постоянного состава 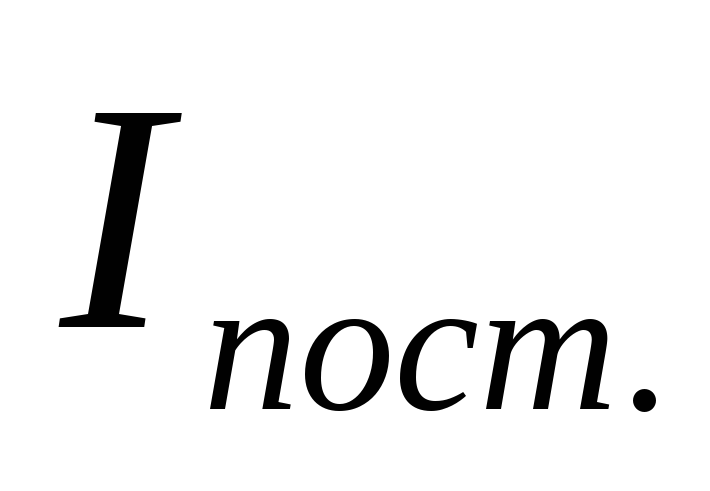
3. Индекс рассчитанных по типу 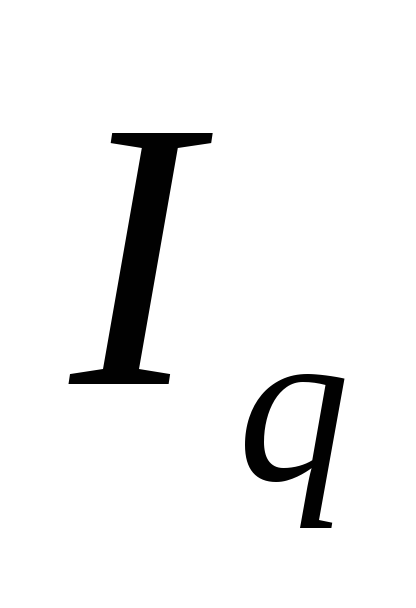
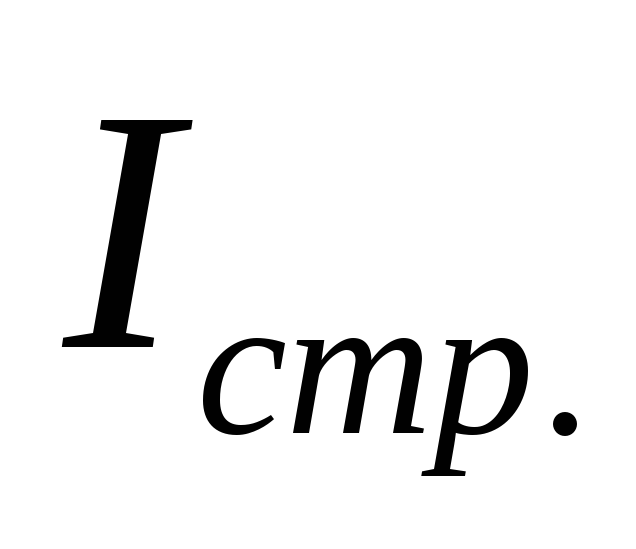
Взаимосвязь: 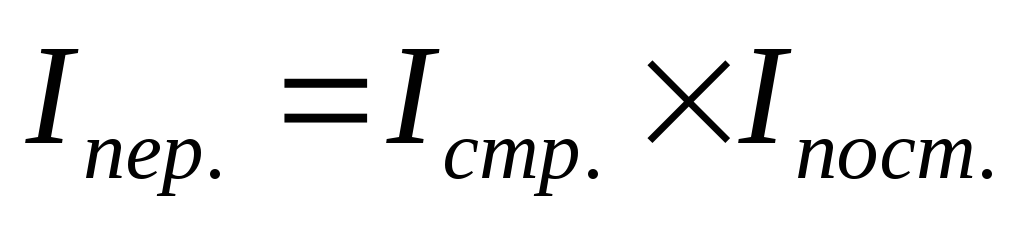
Контрольные вопросы к теме:
1. Расскажите, что такое индекс, перечислите индивидуальные индексы.
2. Назовите формулы общих индексов цены, физического объема и стоимости. Поясните взаимосвязь индексов.
3. Как вычислить абсолютные приросты соответствующие индексам.
4. Какие средние арифметические и средние гармонические индексы вы знаете. Запишите их формулы.
5. Объясните понятия «базисные» и «цепные» индексы. Как проверить их взаимосвязь.
6. Как вычисляются индексы средних величин.
13. Статистическое изучение связей между явлениями
13.1.Типы связей между явлениями, их характеристика
Изучение действительности показывает, что изменение изучаемого признака находится в тесной взаимосвязи с другими признаками.
При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обуславливающих изменения других признаков – они называются факторными признаками (Х).
Признаки, которые являются результатом влияния этих факторных признаков, называются результативными признаками (У).
Например: рассматривая зависимость между производительностью труда и квалификацией рабочих, уровень производительности труда является результативным признаком, а квалификация рабочих факторным, т.к. её повышение ведет к росту производительности труда.
Различают два основных вида связей между явлениями.
– функциональные связи характеризуются полным соответствием между изменением факторного и результативного признака (каждому значению признака – фактора соответствует вполне определенные значения результативного признака) y =f(x).
Примером функциональной связи является зависимость длины окружности (L) от радиуса (r).
– корреляционные связи, при которых между изменением факторного и результативного признаков нет полного соответствия, воздействия отдельных факторов проявляется лишь в среднем при массовом наблюдении, фактических данных.
В простейшем случае применения корреляционной зависимости величина результативного признака рассматривается как следствие изменения только одного фактора (например: рост квалификации рабочих рассматривается как причина роста производительности труда).
Однако выделенный в данном примере в качестве основного признак – фактор не является единственной причиной изменения результативного признака, а на ряду с ним на величину результативного признака влияет множество других причин (в частности на производительность труда влияет уровень энерговооруженности, механизации и автоматизации производства).
При наличии корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака.
Объяснения этому – сложность взаимосвязей между анализируемыми факторами, взаимодействие которых влияют неучтенные, случайные величины. Поэтому связь появляется лишь в среднем, в массе случаев.
Соответствует случайно распределенные в некотором интервале значения функции (у – признака результата).
Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что удобрения участвуют в формировании урожая, для конкретного поля участии одного и того же количества удобрений вызовет разный прирост урожайности, так как во взаимодействии находится ещё целый ряд факторов (погода, состояние почвы и т. д.), которые формируют урожай. Однако в среднем такая связь наблюдается увеличение массы внесенных, удобрений ведет к росту урожайности.
1. По направлению связи делятся на:
– прямые, когда зависимая переменная растёт с увеличением факторного признака (положительная связь)
– обратные, когда рост факторного признака ведёт к уменьшению результативного (отрицательная связь)
2. По степени тесноты:
Величина коэффициента корреляции
До
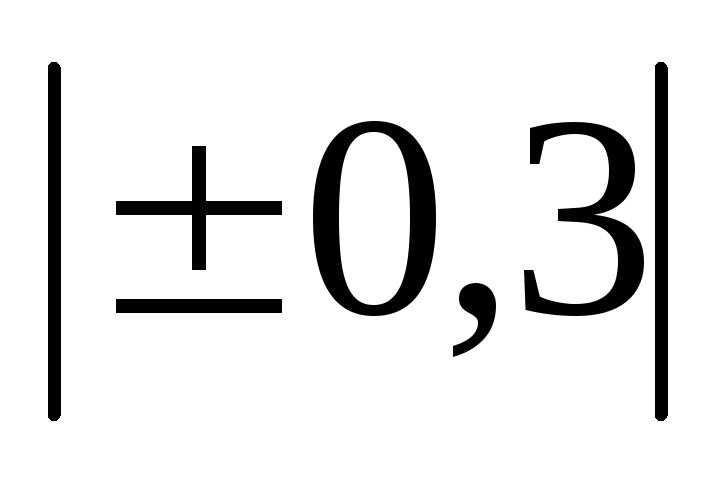
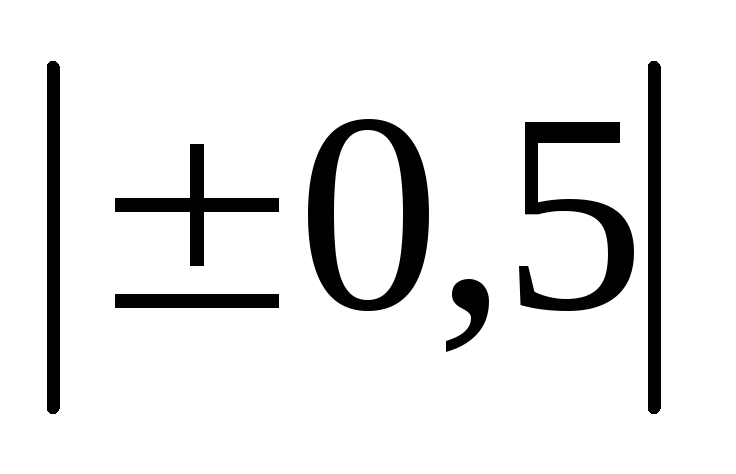
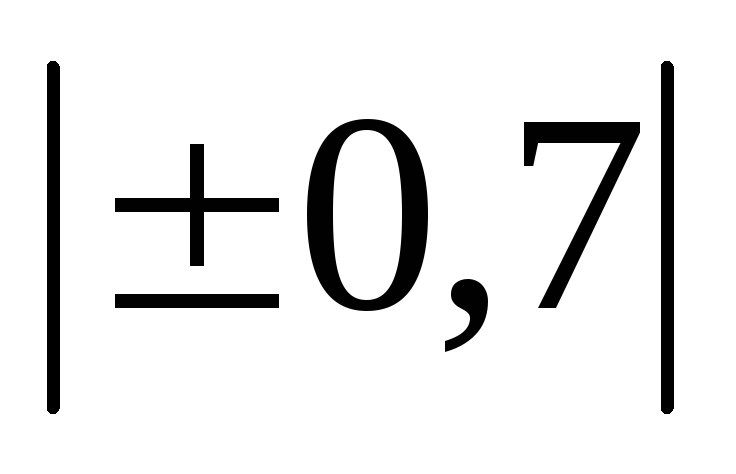
3. По аналитическому выражению: – линейные – криволинейные.
Задачи статистики в изучении связей между явлениями заключается в следующем:
1. Количественная оценка наличия и направления связи.
2. Характеристика формы влияния одних факторов на другие (изменение степени тесноты корреляционной связи).
3. Нахождение аналитического выражения связи (построение уравнений регрессии или корреляционно-регрессионных моделей).
4. Оценка соответствия полученных моделей и их практическое использование.
Методы выявления наличия корреляционной связи между двумя признаками
Для ответа на вопрос о наличии или отсутствии корреляционной связи используется ряд методов:
– параллельное сопоставление рядов значений результативного и факторного признаков, является простейшим приёмом. Значения факторного признака располагаются в возрастающем порядке, а затем прослеживают направление изменения величины результативного признака;
Однако наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие таких параллельных рядов. В таких случаях для установления связи – пользуются статистическими таблицами – корреляционными и групповыми.
Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков.
При этом факторный признак (х), как правило, имеет конкретные значения и располагается в строках; а результативный признак (y) представлен в виде интервалов и располагается в столбцах таблицы.
Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту построения данного сочетания значений Х и Y.
Такая корреляционная таблица уже при общем знакомстве даёт возможность:
а) определить наличие или отсутствие связи;
б) выяснить её направление.
Если частоты в корреляционной таблице расположены по диагонали из левого верхнего угла в правый нижний (т.е. большим значениям фактора соответствуют большие значения результата), то можно предположить наличие прямой корреляционной зависимости между признаками.
Если же частоты располагаются с правого верхнего угла к левому нижнему, то предполагают наличие обратной связи.
Построение групповой таблицы также начинают с группировки. По каждой группе вычисляют средние значения результативного признака, и дальше происходит сопоставление полученных данных.
Графический метод применяется для:
1. Предварительного выявления наличия или отсутствия связи.
2. Определения характера и формы связи.
Используя данные об индивидуальных значениях признака-фактора и соответствующих значениях результативного признака, можно построить в прямоугольных осях точечный график, который называется поле корреляции.
Определив среднее значение точек, можно построить линию, которая является эмпирической линией связи.
Если эмпирическая линия связи приближается к прямой линии связи, то возможно наличие прямолинейной линии корреляционной связи между признаками.
Если к какой-либо кривой, то возможна криволинейная корреляционная связь.