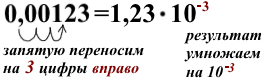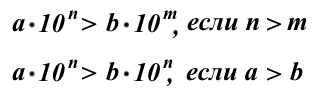Friday, January 30, 2026
Latest:

Компьютерный портал 43413.net

Компьютерный онлайн портал 43413.net по освещению новинок в сфере компьютерных устройств и новинок ИТ.

Компьютерные советы 

какая запись числа называется стандартным его видом

admin 0 Comments

Стандартный вид числа

В данной публикации мы рассмотрим, что такое стандартный вид числа, и как он записывается. Также разберем практические примеры по этой теме.

Запись больших и маленьких чисел

В точных науках время от времени встречаются очень большие или, наоборот, маленькие значения величин. Чтобы было комфортнее работать с ними, и тем более, одновременно использовать вместе в одних и тех же расчетах, был придуман некий общий принцип записи чисел, так называемый стандартный вид.

Чтобы в полной мере усвоить представленный ниже материал, необходимо знать, что такое степень. К примеру, продемонстрируем ее разные варианты на числе 10:

Также напомним, для того, чтобы какое-то число умножить на 10, 100, 1000, 10000 и т.д., мы просто приписываем к нему количество нулей, которое содержится в 10, 100, 1000, 10000 и т.д. Например,

То же самое касается и деления на 10, 100, 1000, 10000 и т.д., только здесь мы убираем нули:

Перечисленные выше действия можно представить в другом виде – как произведение на 10 в определенной степени:

Десятичные дроби

Если мы имеем дело с десятичным дробями, то в целом всё аналогично. При их умножении на 10, 100, 1000 и т.д. мы смещаем запятую-разделитель вправо на столько позиций, сколько нулей содержится в 10, 100, 1000 и т.д.

Если нужно разделить десятичную дробь на 10, 100, 1000 и т.д., то мы смещаем запятую влево на соответствующее нулям количество позиций:

Стандартный вид числа

Натуральное число или десятичную дробь (конечную) в общем виде можно представить следующим образом:

Такая запись и есть стандартный вид числа.

Пример 1
Представим число 2300 в стандартном виде.

Решение:
Первая цифра числа – это 2, она находится между нулем и десятью, что удовлетворяет условию выше.

Ставим после двойки запятую-разделитель и отсчитываем, сколько цифр у нас осталось после нее справа. В нашем случае их три.

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Следовательно, мы умножаем полученную десятичную дробь ( a ) на число 10, степень которого равняется количеству цифр после запятой:

Другими словами, мы умножили дробь на 1000 (10 3 ).

Как мы знаем, в десятичной дроби нули в конце дробной части можно опустить, т.е. финальная запись числа 2300 в стандартном виде выглядит так:

Пример 2
Представим число 0,0029 в стандартном виде.

Решение:
Нам нужно, чтобы до запятой (т.е. слева от нее) стояла цифра от 1 до 9. Следовательно, перемещаем запятую на три позиции вправо.

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Получаем новую десятичную дробь 2,9. Ее нужно умножить на 10, но в отрицательной степени, т.к. мы сделали число кратно больше исходного. Значение степени равняется количеству позиций, на которое была сдвинута запятая, т.е. в нашем случае получается “минус три”.

Источник

Стандартный вид числа

Стандартный вид числа — это его запись в виде произведения

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Число n называется порядком числа, записанного в стандартном виде.

В стандартном виде можно записать любое положительное число.

Как правило, стандартный вид числа используют для записи больших и малых величин.

Записать число в стандартном виде и указать порядок числа:

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Получили число, записанное в стандартном виде. Его порядок n=6.

При решении примеров на приведение числа к стандартному виду удобнее деление числа на

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

заменить умножением на

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Это число записано в стандартном виде. Его порядок n=10.

Чтобы первый множитель соответствовал условию 1≤a какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.

Далее выполняем умножение степеней с одинаковыми основаниями.

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Сравнение чисел, записанные в стандартном виде

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом9,8 \cdot 10^7 \]” title=”Rendered by QuickLaTeX.com”/>

так как порядок первого числа больше порядка второго числа (8>7);

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

поскольку порядок первого числа меньше порядка второго числа (-8 какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом2,97 \cdot 10^9 \]” title=”Rendered by QuickLaTeX.com”/>

так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).

Источник

Стандартная запись числа

Определение стандартного вида числа

Стандартным видом числа b называют его запись в виде

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Оперировать числами в стандартном виде намного удобней, чем пересчитывать и переписывать бесчисленные нули слева или справа.

На рисунке вверху показан результат работы программы, находящей решение 128 линейных уравнений с 128 неизвестными.

Алгоритм записи числа в стандартном виде

Найдём, сколько секунд в году, и запишем результат в стандартном виде:

$$ 365 \frac<день> <год>\cdot 24 \frac<ч> <день>\cdot 3600 \frac<с> <ч>= 31536000 \frac<с> <год>= 3,1536 \cdot 10^7 \frac<с> <год>$$

Шаг 1. Поставить в данном числе новую запятую так, чтобы в целой части осталась одна, отличная от нуля, цифра.

Сравнение чисел, записанных в стандартном виде

Сравниваем два положительных числа:

Число с большим порядком больше числа с меньшим порядком:

Если порядки одинаковы, то сравнивают мантиссы:

Примеры

Пример 1. Выполните действия и запишите результат в стандартном виде:

$ б) (9,3 \cdot 10^<-9>)^2:(3 \cdot 10^ <-10>) = \frac<9,3^2> <3>\cdot 10^ <-18+10>= 28,83 \cdot 10^ <-8>= 2,883 \cdot 10^ <-7>$

Пример 2. Сравните числа:

$а) 5,8 \cdot 10^9 и 4,7 \cdot 10^<10>$

Порядки чисел одинаковы, мантисса первого числа больше.

$ в) 3,7 \cdot 10^ <-8>и 2,5 \cdot 10^<-9>$

$г) 2,1 \cdot 10^ <-7>и 2,5 \cdot 10^<-7>$

Порядки чисел одинаковы, мантисса второго числа больше.

Пример 3. Найдите массу одной молекулы углекислого газа в граммах.

Количество молекул газа в одном моле определяется числом Авогадро:

Пример 4. Космический аппарат «Вояджер-1» находится сейчас (март 2020 г.) на расстоянии 148,56 а.е. от Земли (https://voyager.jpl.nasa.gov/mission/status/). Через сколько часов мы принимаем радиосигнал после того, как он был передан аппаратом?

1 а.е. (астрономическая единица) = 149 597 870 700 м \approx 1,496 \cdot 10^ <11>м

Скорость распространения радиосигнала (скорость света)

$ c = 299 792 458 \frac<м> <с>\approx 3 \cdot 10^8 \frac<м><с>$

Получаем время приёма:

Таким образом, «Вояджер-1» спустя 43 года находится от нас на расстоянии ≈ 20,6 световых часов.

Пример 5. Космический аппарат «Вояджер-1» спустя 43 года находится от Земли на расстоянии 20,6 световых часов (см. Пример 4). Сколько тысячелетий ему понадобится, чтобы с такой скоростью добраться до ближайшей звезды Проксима Центавра, которая расположена примерно в 4,244 световых года от нас?

Переведём световые годы в световые часы:

$4,244 св.г = 4,244 \cdot 365 \cdot 24 св.ч \approx 3,718 \cdot 10^4 св.ч$

Источник

Стандартная форма записи числа, мантисса числа, порядок числа

Положительное число, записанное в стандартной форме, имеет вид

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом,

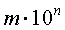
Число m является натуральным числом или десятичной дробью, удовлетворяет неравенству

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом,

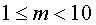
и называется мантиссой числа, записанного в стандартной форме.

Число n является целым числом (положительным, отрицательным или нулем) и называется порядком числа, записанного в стандартной форме.

Например, число 3251 в стандартной форме записывается так:

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом,

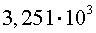
Здесь число 3,251 является мантиссой, а число 3 является порядком.

Стандартная форма записи числа часто используется в научных расчетах и очень удобна для сравнения чисел.

Для того, чтобы сравнить два числа, записанных в стандартной форме, нужно сначала сравнить их порядки. Большим будет то число, порядок которого больше. Если же порядки сравниваемых чисел одинаковы, то нужно сравнить мантиссы чисел. Большим в этом случае будет то число, у которого мантисса больше.

Например, если сравнить между собой записанные в стандартной форме числа

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видоми какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом,

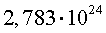
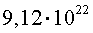
то, очевидно, первое число больше второго, поскольку у него порядок больше.

Если же сравнить между собой числа

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видоми какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом,

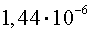
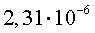
то, очевидно, что второе число больше, чем первое, поскольку порядки у этих чисел совпадают, а мантисса у второго числа больше.

Источник

КОНСПЕКТ УРОКА 8 КЛАСС по алгебре “СТАНДАРТНЫЙ ВИД ЧИСЛА”

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Описание презентации по отдельным слайдам:

Стандартный вид числа

ВЫРАЗИТЬ: 50 кг в граммах; 150 т в килограммах; 130 см в метрах; 2 м в миллиметрах; 15 грамм в килограммах. a) а-6·а·а-4 =__; в) (a-4)-2 =__; д) (2a3)-3 =__; б) a-8 : a-5 =__; г) а-15: а-15 =__; е) а-3·а=__.

В науке и технике астрономы, физики, химики, биологи ставят эксперименты, затем исследуют получившиеся результаты и получают очень большие и очень малые числа. Математики в своем научном творчестве часто помогают им решать различные задачи, используя теорию больших и малых чисел. Например, большим числом выражается масса Земли – 5 980 000 000 000 000 000 000 т. Малым числом выражается размер вируса гриппа равен 0, 000000103 м

миллион (6 нулей) 1000000 миллиард (9 нулей) 1000000000 триллион (12 нулей) 1000000000000 квадриллион (15 нулей)1000000000000000 квинтиллион (18 нулей) 1000000000000000000 секстиллион (21 нулей) 1000000000000000000000 септиллион (24 нулей) 1000000000000000000000000 октиллион (27 нулей) 1000000000000000000000000000 нониллион (30 нулей) 10000000000000000000000000000000 дециллион (33 нуля) 10000000000000000000000000000000000

Какая запись называется стандартным видом числа? Как называется число n в этой записи? Что показывает большой положительный порядок в стандартной записи числа? Что показывает большой по модулю отрицательный порядок?

матисса (число а) порядок (число n)

З а д а н и е. Определить, какие из чисел записаны в стандартном виде, а какие – нет. Ответ объяснить: а) 2,3 · 109; б) 1,23 · 10–11; в) 15 · 1014; г) 8 · 10–5; д) 4,2 · 1005; е) 5,8 · 1023; ж) –3 · 10–15; з) 0,24 · 10–17; и) 10 · 104.

Представим в стандартном виде числа α=4350000. В числе α поставим запятую так, чтобы в целой части оказалась одна цифра. В результате получим 4,35. отделив запятой 6 цифр справа, мы уменьшили число α в раз. Отсюда α =

Представим в стандартном виде число α=0,000508. В числе α представим запятую так, чтобы в целой части оказалась одна отличная от нуля цифра. В результате получится 5,08. представив запятую на 4 знаков вправо, мы увеличили число α в раз. Поэтому число α меньше числа 5,08 в раз. Отсюда α =

1) Представьте число 3540000 в стандартном виде. 2) Представьте число 0,00248 в стандартном виде.

4) Представьте число 125,3 в стандартном виде. 3) Представьте число 6215 в стандартном виде. 5) Представьте число 0,0000125 в стандартном виде. 6) Представьте число 0,0456 в стандартном виде.

НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ:

2)Умножение чисел, записанных в стандартном виде. Чтобы перемножить числа, записанные в стандартном виде надо: Умножить числовую часть числа на числовую, а степенную часть на степенную. Полученные произведения перемножить.

200 0,03 0,003 НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ:

Деление чисел, записанных в стандартном виде. Чтобы разделить числа, записанные в стандартном виде надо: Разделить числовую часть числа на числовую, а степенную часть на степенную. Полученные произведения перемножить.

0,07 30 0,0008 НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ:

4)Возведение в степень чисел, записанных в стандартном виде. Чтобы возвести в степень числа, записанные в стандартном виде надо: Возвести в данную степень числовую и степенную часть данного числа. Полученные произведения перемножить.

НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ:

Какая из планет ближе к Солнцу? Какая из них расположена дальше всех от Солнца? Расположите планеты в порядке удаления от солнца. Приведены расстояния до Солнца. Планета Расстояние, км Венера 1,082 *108 Земля 1,495*108 Меркурий 5,790*107 Марс 2,280*108 Нептун 4,497*109 Плутон 5,947*109 Сатурн 1,427*109 Уран 2,871*109 Юпитер 7,781*108

ВОТ И ЗАВЕРШАЕТСЯ НАШ УРОК. СПАСИБО ЗА УРОК! До свидания! ПОДВЕДЕМ ИТОГИ: С какой темой мы сегодня познакомились? Как формулируется эта тема? Какую запись числа называют его стандартным видом? Записаны ли числа 11 · 108 и 0,93 · 10–5 в стандартном виде? Почему? Если число записано в стандартном виде, что называется его порядком, матиссой? Для чего на практике применяется запись чисел в стандартном виде? Оцените работу вашего партнёра и себя.

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Номер материала: ДБ-1493337

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Гинцбург анонсировал регистрацию детской вакцины от COVID-19

Время чтения: 1 минута

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Школьников не планируют переводить на удаленку после каникул

Время чтения: 1 минута

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Время чтения: 1 минута

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

В Хабаровске утвердили дополнительные школьные каникулы

Время чтения: 1 минута

какая запись числа называется стандартным его видом. Смотреть фото какая запись числа называется стандартным его видом. Смотреть картинку какая запись числа называется стандартным его видом. Картинка про какая запись числа называется стандартным его видом. Фото какая запись числа называется стандартным его видом

Минобрнауки намерено ввести углубленное изучение климата в вузах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

You May Also Like

код ответа http 401

admin 0

Лунго кофе что за вкус

admin 0

код должности главный специалист эксперт

admin 0

Leave a Reply

Your email address will not be published. Required fields are marked *