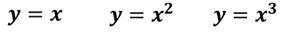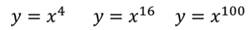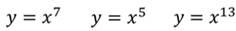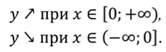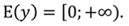Нечетная функция имеет 4 нуля докажите что 0 не принадлежит области определения
Нечетная функция имеет 4 нуля. Четность и нечетность функций
Способы задания функции
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Четная и нечетная функция
Исследуем на четность нижеприведенную функцию:
Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.
Периодическая функция
f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty)
Промежутки, где функция отрицательная, то есть f(x) (-\infty; x_<1>) \cup (x_<2>; x_<3>)
Ограниченность функции
Возрастающая и убывающая функция
Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x)
Функция y=x^n
Урок 9. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Функция y=x^n»
Существуют два случая степенной функции: с чётным показателем и с нечётным показателем.
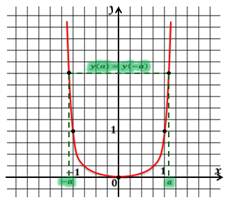
Рассмотрим пример: найти на рисунке степенные функции с чётным показателем и с нечётным показателем.
С чётным показателем:
С нечётным показателем:
Областью определения любой степенной функции с натуральным показателем является множество всех действительных чисел.
Опишем свойства этой функции:
2. Если x≠0, то y>0, т.к. чётная степень как положительного, так и
отрицательного числа положительна.
3. Противоположным значениям аргумента соответствуют равные значения функции.
4. Функция возрастает и убывает на промежутке:
5. При любых значения аргумента функция принимает неотрицательные значения. Областью значений является:
График выглядит так:
Опишем свойства этой функции:
1. Если x=0, то y=0. Ноль в любой степени равен нулю.
Четные и нечетные функции
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Тема урока. «Чётность и нечётность функций. Нулевые функции».
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
АЛГЕБРА И НАЧАЛА АНАЛИЗА.
Тема урока. «Чётность и нечётность функций. Нулевые функции».
Образовательные: повторить основные теоретические понятия: четность и нечётность функций, свойство графика четной и нечётной функции, четность и нечетность тригонометрических функций. Изучить понятие нулевой функции, свойство графика нулевой функции, построить алгоритм исследования функции на четность и нечетность, сформировать умение променять его при решении примеров.
Развивающие: формирование умения наблюдать, проводить рассуждения по аналогии, обобщать, развивать логическое и творческое мышление.
Воспитательные: совершенствовать навыки коллективной работы, развивать умение анализировать ситуацию, выделять главное, сопоставлять факты. Развивать ассоциативное мышление.
Оборудование : компьютер, интерактивная доска, карточки для работы по группам, индивидуальные карточки для самостоятельной работы.
Орг. момент. (Психологический настрой на урок).
Проверка домашнего задания.
Дать определение чётной функции.
её область определения симметрична относительно нуля;
Дать определение нечётной функции.
её область определения симметрична относительно нуля;
Сформулировать свойства графика чётной функции.
График чётной функции симметричен относительно оси ординат.
Сформулировать свойства графика нечётной функции.
График нечётной функции симметричен относительно начала координат.
Что вы можете сказать о чётности и нечётности тригонометрических функций.
Каждой группе было дано домашнее задание: исследовать функции на чётность и нечётность. По одному представителю от каждой группы выходят к доске.
+3
f(-x) = cos(-4x) + 4cos(-2x) –
= cos4x +4cos2x – 
+ 3 = f(x);
f(x) – чётная функция.
g(x) – нечётная функция.
Функция h ( x ) не является ни чётной, ни нечётной функцией.
Устно. ( Графики отображаются на экране).
1.Какая из указанных функций является:
1) нечетной; 2) четной; 3) не является ни четной ни нечетной?
2.Определить, какие из указанных функций являются чётными и нечётными:
Как можно изменить функцию f (х), что бы она стала ни четной ни нечётной?
-Можно прибавить число.
— Можно степень заменить на четную.
— Можно синус заменить на косинус.
2) 
; (область определения все числа и f (- x ) = f ( x ),четная).
Если к функции прибавить или отнять число, как это повлияет на четность?
-Функция останется четной.
3) h (х) = 5. (область определения все числа, четная).
( После устного счета отвечают те учащиеся, кто работал у доски).
Изучение новой темы.
Каждой группе было предложено задание на дом, упростить данные выражения. На уроке информатики Андрей Владимирович помог ребятам оформить решение каждого примера на компьютере в виде презентации.
— + 3 = 2 cos ² 2 x – 1 + +4cos2x+3 – = 
g(x) = sinxcos3xcos4x – 0,25(sin8x – sin6x+ sin2x) = 0,5(sin4x – sin2x)cos4x –
— 0,25(sin8x – sin6x + sin2x) =
— 0,25(sin8x – sin6x + sin2x) = 0.
-Ребята, мы видим, что, в третьем случае после преобразования выражения, задающего функцию h (х), мы получили h (х) = 1. Изобразите на доске график этой функции.
Из третьей группы ученик рисует на доске график функции h (х) = 1.
(На доске изображена заготовка прямоугольной системы координат).
y
Какой же является данная функция?
-Данная функция является четной.
— Вернемся к примерам 1-ой и 2-ой группы. Мы получили функции, области значения которых включают только 0. Такие функции называются нулевыми функциями
(На доске дописывается тема урока: «Нулевые функции»)
— Ребята, кто из вас ещё раз сформулирует определение нулевой функции.
Функция, область значения которой равна нулю, называется нулевой функцией.
— Как вы считаете, что будет являться графиком нулевой функции?
Графиком нулевой функции является ось абсцисс.
(Учащиеся пишут определение и строят график в тетрадь, одновременно определение и график функции отображается на экране).
— Как вы считаете, относительно чего симметрична данная прямая?
Прямая y = 0 симметрична как относительно оси ординат, так и относительно начала координат.
— Если графики нулевых функции f и g симметричны относительно начала координат, то функции f и g являются какими?
— Если графики функций f и g симметричны относительно оси ординат, то функции f и g являются какими?
— Какой можно сделать вывод на основании этих двух утверждений?
На основании этих утверждений заключаем, что функции f и g являются и чётными, и нечётными.
— Итак, функции f и g – нулевые и они являются и чётными и нечётными. Вместе с тем, возникает вопрос, а могут ли функции, являющиеся и чётными и нечётными, быть отличными от нулевых?
Чтобы ответить на этот вопрос, докажем утверждение: «Только нулевые функции могут быть и чётными, и нечётными».
(Данное утверждение и доказательство отображается на экране, учащиеся записывают их в тетрадь).
-Отсюда делаем вывод: только нулевые функции могут быть и чётными, и нечётными.
1.Учащиеся работают по группам (Каждая группа получает карточку).
I группа. Исследовать на чётность и нечётность функцию 
и построить её график.
Решение: Область определения этой функции составляют все числа, кроме 0. А при х ≠ 0 имеем: 
Значит, данная функция является нулевой. Построим график этой функции. По графику видно, что она является и чётной, и нечётной. Кроме того, данная нулевая функция является разрывной.
Исследовать на чётность и нечётность функцию 
и построить её график.
Область определения этой функции составляют все числа, кроме х = 1. А при х ≠ 1 имеем: 
Следовательно, данная функция является нулевой. Её график представлен на рисунке.
y
Область определения данной функции есть множество, несимметричное относительно начала координат. Значит, данная функция, являясь нулевой, не является ни чётной, ни нечётной.
— Нулевых функций, которые задаются формулами
, где 
, существует бесконечное множество, т. е. существует бесконечное множество функций, которые являясь нулевыми, не являются и четными и нечетными.
Исследовать на чётность и нечётность функцию 
и построить её график.
y
Область определения данной функции есть множество, симметричное относительно начала координат и данная функция является нулевой. Значит она является и чётной, и нечётной.
2. При решении задач на определение четности и нечетности функций удобно пользоваться следующим алгоритмом.
Нечетная функция имеет 4 нуля. Четность и нечетность функций
Читайте также
Способы задания функции
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Четная и нечетная функция
Исследуем на четность нижеприведенную функцию:
Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.
Периодическая функция
f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty)
Промежутки, где функция отрицательная, то есть f(x) (-\infty; x_<1>) \cup (x_<2>; x_<3>)
Ограниченность функции
Возрастающая и убывающая функция
Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x) 0 при х > 0,4 ; f (х ) –1
– Выполняя данную работу, ребята мы выявили ещё одно свойство функции, незнакомое вам, но не менее важное, чем остальные – это чётность и нечетность функции. Запишите тему урока: «Чётные и нечётные функции», наша задача – научиться определять чётность и нечётность функции, выяснить значимость этого свойства в исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем (стр. 110). Слайд
Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд
Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.
– У чётных функций область определения – симметричное множество? У нечётных?
– Если же D(f ) – несимметричное множество, то функция какая?
– Таким образом, если функция у = f (х ) – чётная или нечётная, то её область определения D(f ) – симметричное множество. А верно ли обратное утверждение, если область определения функции симметричное множество, то она чётна, либо нечётна?
– Значит наличие симметричного множества области определения – это необходимое условие, но недостаточное.
– Так как же исследовать функцию на четность? Давайте попробуем составить алгоритм.
Алгоритм исследования функции на чётность
1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.
2. Составить выражение для f (– х ).
1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.
2) h (– х) = (–х) 5 + – х5 –= – (х 5 +),
3) h(– х) = – h (х) => функция h(х) = х 5 + нечётная.
у = f (х ), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.
а) у = х 2 · (2х – х 3), б) у =
Постройте график функции у = f (х ), если у = f (х ) – нечётная функция.
Взаимопроверка по слайду.
6. Задание на дом: №11.11, 11.21,11.22;
Доказательство геометрического смысла свойства чётности.
***(Задание варианта ЕГЭ).
1. Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(х ) = х (х + 1)(х + 3)(х – 7). Найдите значение функции h(х ) = при х = 3.
7. Подведение итогов
График четной функции симметричен относительно оси \(y\) :
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
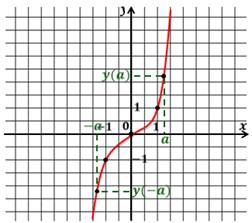
Пример: у функции \(f(x)=\sqrt x+1\) область определения: \(x\in
Уровень задания: Равен ЕГЭ
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
Уровень задания: Равен ЕГЭ
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
Уровень задания: Равен ЕГЭ
(Задача от подписчиков)
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrtx\) проходил через точку \(A\) :
2) Пусть \(a \[\dfrac<64>9a=|a+2|\cdot \sqrt <-8>\quad\Leftrightarrow\quad \left[\begin
Уровень задания: Равен ЕГЭ
имеет хотя бы один корень.
(Задача от подписчиков)
Уровень задания: Равен ЕГЭ
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \
имело четыре различных корня, отличных от нуля, представляющих вместе с \(x=0\) арифметическую прогрессию.
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \ Решая данную совокупность систем, получим ответ: \\]