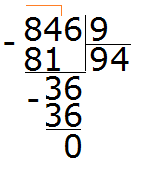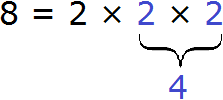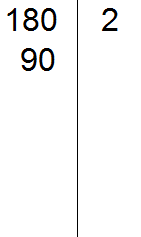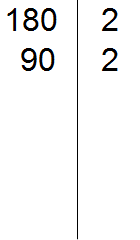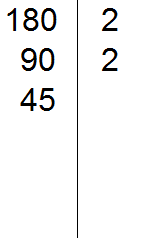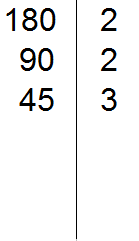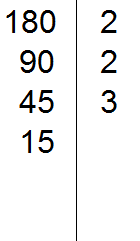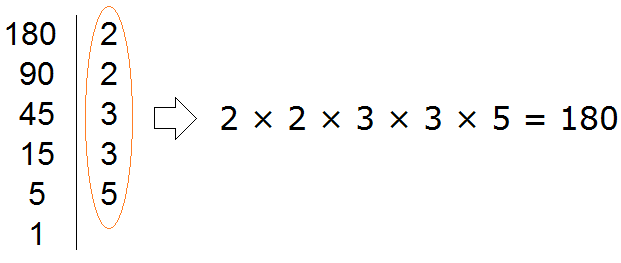Нечетная кратность что такое

Четные и нечетные числа — определение, признаки и свойства

Одной из характеристик числа является его кратность двум. Простое арифметическое свойство стало основой для мистических верований древних людей, служит фундаментом для быстрых алгебраических вычислений и геометрических формул. Нечетные и четные числа широко используются современным человеком в повседневной жизни.

Арифметические свойства

Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.

Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.

Закономерности арифметических операций с целыми числами:

Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.

При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.

Характеристика парности у ноля

Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.

В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.

Признаки четности ноля:

Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.

Свойства группы для вычислений

Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.

Алгоритм оптимизированного решения:

Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.

Примеры логических задач для решения через характеристику парности:

Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.

Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.

История и значение в культуре

Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.

Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.

Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.

У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.

Практическое применение

Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.

В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.

Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

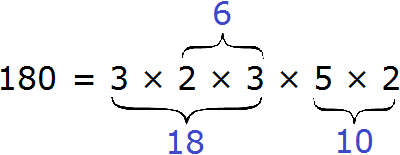
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

Например, разложим предыдущее число 180 этим способом.

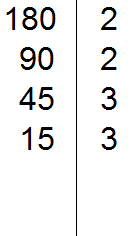
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

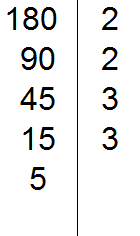
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

5 не делится на 3. Тогда проверяем делится ли 5 на 5.

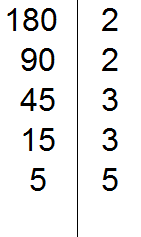
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

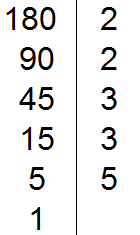
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

Пример 1. Найти делители числа 12

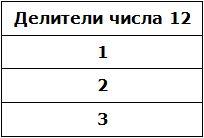
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

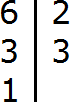
Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник

Решение рациональных неравенств методом интервалов

1. Непрерывная функция g(x) может изменить знак только в той точке, в которой она равна 0. Графически это означает, что график непрерывной функции может перейти из одной полуплоскости в другую, только если пересечет ось абсцисс (мы помним, что ордината любой точки, лежащей на оси ОХ (оси абсцисс) равна нулю, то есть значение функции в этой точке равно 0):

Мы видим, что функция меняет знак в корне знаменателя, в точке , но при этом не обращается в ноль ни в одной точке. Таким образом, если функция содержит дробь, она может менять знак в корнях знаменателя.

2. Однако, функция не всегда меняет знак в корне числителя или в корне знаменателя. Например, функция y=x 2 не меняет знак в точке х=0:

Т.к. уравнение x 2 =0 имеет два равных корня х=0, в точке х=0 функция как бы дважды обращается в 0. Такой корень называется корнем второй кратности.

Функция меняет знак в нуле числителя, , но не меняет знак в нуле знаменателя: , так как корень — корень второй кратности, то есть четной кратности:

Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры, как правило, решается с помощью метода интервалов.

1. Для начала необходимо привести неравенство к виду

Р(х)V0,

а) перенести все слагаемые в левую часть неравенства,

б) найти корни получившегося выражения,

в) разложить левую часть неравенства на множители

г) одинаковые множители записать в виде степени.

2. Нанести найденные корни на числовую ось.

3. Если неравенство строгое, то кружки, обозначающие корни на числовой оси оставляем «пустыми», если неравенство нестрогое, то кружки закрашиваем.

5. Определяем знак Р(х) на самом правом промежутке. Для этого берем произвольное значение х₀, которое больше большего корня и подставляем в Р(х).

Если P(x₀)>0 (или ≥0), то в самом правом промежутке ставим знак «+».

Если P(x₀)

(где V- знак неравенства: )

Строгое неравенство такого вида равносильно неравенству

НЕстрогое неравенство вида

равносильно системе:

На практике, если функция имеет вид , то поступаем следующим образом:

Чтобы лучше понять алгоритм решения неравенств методом интервалов, посмотрите ВИДЕОУРОК, в котором подробно разбирается пример решения неравенства методом интервалов.

Источник