Несколько прямых на плоскости пересекаются так что через каждую точку их пересечения
Ответы 2
«слове о полку игореве» мне нравятся практически все герои. основной персонаж здесь сам князь игорь святославич. и лично у меня он вызывает симпатию. возможно, многие его осудят за желание прославиться, за то, что он пошёл на половцев без подмоги. многие также осудят его и за излишнюю самоуверенность. ведь в результате он проиграл битву, потеряв своё войско, и сам оказался в плену. то есть его самоуверенность и желание прославиться сыграли с ним злую шутку. но, несмотря на всё это, я вижу игоря святославича достойным сыном отечества и настоящим патриотом своей родины.
меня восхищает его настоящее мужество и отвага, самоотверженное движение к цели. ведь он не только хотел славы, он также искренне стремился к тому, чтобы одержать победу над врагом. все мы в жизни совершаем ошибки, но ведь князь раскаялся в том, что причинил родной земле страдания, раскаялся в том, что был участником междоусобных воин.
как мудрый правитель и хороший наставник предстаёт перед нами князь святослав киевский. он имеет внутреннюю культуру, хорошо знаком с страны, её нравственными корнями. он призывает всех к объединению, к прекращению междоусобных войн, ратует за примирение. у меня этот герой вызывает только светлые чувства и эмоции.
также мне понравился и всеволод, который вместе с игорем пошёл на половцев. как и игорь, он отличался бесстрашием и не побоялся отправиться в поход на половцев. своей отвагой и преданностью всеволод вызвал у меня восхищение.
нельзя не упомянуть и о ярославне. это жена игоря. она безумно любила своего мужа и ждала его. она была готова сделать всё возможное, чтобы её возлюбленный вернулся целым и невредимым. такими искренними чувствами просто невозможно не восхищаться! в наше время нечасто встретишь такую верность.
к отрицательным героям произведения я, конечно, отношусь плохо. здесь такими представлены половцы и их ханы, они были врагами для наших земель и, конечно, относиться к ним хорошо нельзя. когда я читал это произведение, во мне как будто появился дух патриотизма, и мне захотелось пойти на половцев вместе с князем игорем, хоть природа и подавала не хорошие знаки.
Помогите пожалуйста с геометрией!
Две плоскости α и β пересекаются по прямой m. Прямая a лежит в плоскости α, прямая b– в плоскости β. Эти прямые пересекаются в точке А. докажите, что точка А лежит на прямой m.
Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.
Докажите, что если через две параллельные прямые проходят пересекающиеся плоскости, то линия пересечения параллельна каждой из двух прямых или совпадает с одной из них.
Все точки прямой a принадлежат плоскости α, все точки прямой b принадлежат плоскости β, значит точка их пересечения принадлежит обеим плоскостям, а все такие точки лежат на прямой m.
Пусть это не так. Очевидно, что прямая не может пересекать прямую пересечения плоскостей, так как в этом случае она не будет параллельна плоскостям. Пусть они скрещиваются. Через прямую, скрещивающуюся с данной можно провести только одну плоскость, параллельную данной прямой, значит, 2 плоскости совпадают. Противоречие.
Пусть прямые не совпадают с прямой пересечения плоскостей. Если одна из них пересекает данную прямую, то она пересекает и плоскость, в которой лежит вторая прямая, следовательно прямые скрещиваются.
Если обе прямые пресекают прямую персечения, то они либо скрещиваются либо пересекаются. В этих вариантах мы пришли к противоречию, значит либо прямая пересечения параллельна обеим прямымы, либо совпадает с одной из них и параллельна второй.
Комбинаторная задача о числе точек пересечения прямых
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Комбинаторная задача о числе точек пересечения прямых
Известная комбинаторная задача 1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006. 2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка “Первого сентября”. Математика. Вып. 5 (11)). – М.: Чистые пруды, 2006.
Задача о количестве точек пересечения n прямых На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых. Пример. n=5, 10 точек пересечения
Цели работы 1) обобщить одну из известных комбинаторных задач по геометрии и получить полное решение новых задач; 2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.
Задача 1. Наличие параллельных прямых На плоскости провели n прямых, среди которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=8, k=3 25 точек пересечения Пример 2. n=8, k=4 22 точки пересечения
О методе рекуррентных соотношений Метод сведения комбинаторной задачи к аналогичной задаче для меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений. Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д. Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.
Решение задачи №1 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k
Нахождение числа точек пересечения
Таблица и рекуррентные соотношения k m Параллельные прямые 2 3 4 5 Прямые общего положения 1 2 3 4 5 2 5 7 9 11 3 9 12 15 18 4 14 18 22 26 5 20 25 30 35
Задача 2. Наличие пар параллельных прямых На плоскости провели n прямых, среди которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=5, k=2 19 точек пересечения Пример 2. n=6, k=3 33 точки пересечения
Решение задачи №2 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k
Нахождение числа точек пересечения
Таблица и рекуррентные соотношения k m Пары параллельных прямых 2 3 4 5 Прямые общего положения 1 2 8 18 32 2 5 13 25 41 3 9 19 33 51 4 14 26 42 62 5 20 34 52 74
СПАСИБО ЗА ВНИМАНИЕ!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1492120
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Псковских школьников отправили на дистанционку до 10 декабря
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Оренбурге школьников переведут на дистанционное обучение с 9 декабря
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве
Время чтения: 1 минута
ДНР полностью перешла на стандарты и программы России в образовании
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Волжский класс
Боковая колонка
Рубрики
Видео
Книжная полка
Малина для Админа
Боковая колонка
Опросы
Календарь
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Ноя | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
5 класс. Математика. Никольский. Учебник. Ответы к стр. 80
Измерение величин
Прямая. Луч. Отрезок
Ответы к стр. 80
346. Проведите прямую AB и вне ее точку C. Через точку C проведите прямую параллельную прямой AB.
347. Сколько прямых можно провести через одну точку?
348. Даны три точки, не лежащие на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
349. Даны четыре точки так, что никакие три из них не лежат на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
350. На сколько частей прямая делит плоскость?
351. На сколько частей делят плоскость две прямые, если они:
а) пересекаются; б) параллельны?
а) на 4 части;
б) на 3 части.
352. На сколько частей можно разделить плоскость тремя прямыми?
Если прямые параллельны — на 4 части, если пересекаются в одной точке — на 6 частей, если пересекаются не в одной точке — на 7 частей.
353. Отметьте на листе бумаги точку, проведите несколько лучей с началом в этой точке. Сколько таких лучей можно провести?
354. Отметьте на прямой две точки A и B. Сколько получилось лучей с началом в этих точках?
355. Сколько получится лучей, если на прямой отметить:
а) 3 точки; б) 5 точек; в) 100 точек?
Из одной точки выходят два луча.
а) 3 • 2 = 6 лучей;
б) 5 • 2 = 10 лучей;
в) 100 • 2 = 200 лучей.
356. Две прямые пересекаются в одной точке. Сколько лучей с началом в этой точке они образуют?
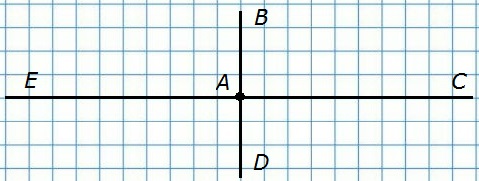
Лучи АС, АD, АЕ, АВ — всего 4 луча.
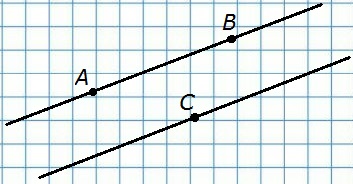
357. Назовите все лучи с вершиной в точках A, B и C (рис. 47). Сколько лучей получилось.

Лучи АM, АN, BM, ВN, CM, CN — всего 6 лучей.
358. Назовите все отрезки с концами в точках M, N и K (рис. 48). Сколько отрезков получилось?

Отрезки MА, MК, NК — всего 3 отрезка.
359. На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте.

Отрезки АВ, АС, АD, ВС, ВD, СD — всего 6 отрезков.
360. Перечертите рисунок 49 в тетрадь. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость? Выберите правильный ответ:
A. 10 частей;
Б. 11 частей;
В. 12 частей.
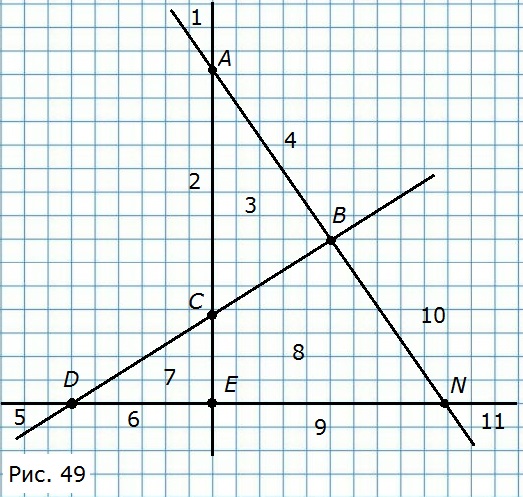
Ответ Б — 11 частей.
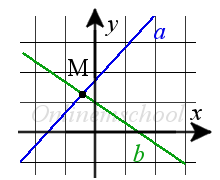
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Вычтем из первого уравнения второе
Из первого уравнения найдем значение x
Подставим значение x во второе уравнение и найдем значение y
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
В первое уравнение подставим значения x и y из второго и третьего уравнений.
Подставим значение t во второе и третье уравнение
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Из второго уравнения выразим y через x
Подставим y в первое уравнение
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
Вычтем из первого уравнения второе
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
Решение: Составим систему уравнений
К шестому уравнению добавим пятое уравнение
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
Подставим значение t из шестого уравнения в остальные уравнения