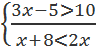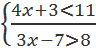Неверно что число 17 делится на 3 логическая связка

Конъюнкция и дизъюнкция высказывательных форм

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) Ù В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В (х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х)ÙВ(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить Т_А – множество истинности предложения А(х), Т_В – множество истинности предложения В(х), а множество истинности их конъюнкции Т_А˄В, то, по всей видимости, Т_А˄В = Т_А Т_В.

Докажем это равенство.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т_А Т_В. По определению пересечения множеств это означает, что а ∈ Т_А и а ∈ Т_В, откуда получаем, что А(х) и В(х) – истинные высказывания, поэтому конъюнкция высказываний А(х)˄В(х) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)˄В(х), т.е. а ∈ Т_А˄В. Таким образом, мы доказали, что Т_А Т_В ∈ Т_А˄В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства Т_А˄В = Т_А Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Приведем примериспользования этого правила. Найдем множество истинности конъюнкции двух неравенств 2х > 10 и 4+х 10 ˄ 4+х 10, а Т₂ – множество решений неравенства 4+х

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характеристических свойств данных множеств:

А B = <х½х∈A ˄ х∈B>, А B = <х½х∈A ˄ х∈B>, причем каждое свойство представляет собой высказывательную форму.

Упражнения

1. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30.

Выпишите все числа, в записи которых:

1) три цифры и есть цифра 3;

2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые:

1) двузначные или меньше 17;

2) двузначные и меньше 17.

в) Из ряда 72,312,522,483,1137 выпишите те числа, которые:

1) делятся на 3 и 9;

2) делятся на 3 или на 9.

2. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из:

1) прямоугольных и равнобедренных треугольников;

2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых:

1) диагонали равны и есть прямой угол;

2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые:

1) делятся на 4 и больше 12;

2) делятся на 4 или 12.

3. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а)

б)

4. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ∈ R. Использовалось ли вами понятие дизъюнкции высказывательных форм?

5. Вместо многоточия вставьте «и» либо «или»:

а) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

б) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

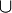
6. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

Источник

Математика для учащихся колледжа

Математические предложения План Высказывания и высказывательные формы. Значение истинности высказываний и высказывательных форм. Простые и составные высказывания и высказывательные формы. Логическая структура составного предложения. Конъюнкция и дизъюнкция высказываний Таблица истинности высказываний. Конъюнкция и дизъюнкция высказывательных форм. Высказывания с кванторами. Квантор общности и значение истинности. Квантор существования и значение истинности. Отрицание высказываний и высказывательных форм. Отношения следования и равносильности. Структура и виды теорем. Теорема, правила, формулы Виды теорем. Закон контрпозиции Основные выводы

Просмотр содержимого документа
«Математика для учащихся колледжа»

Рассмотрим некоторые предложения

Определим истинны ли они или ложные

Предложения 1,2,4 – истинные

Предложение 3 – ложное

Предложение 5 – нельзя указать истинное оно или ложное

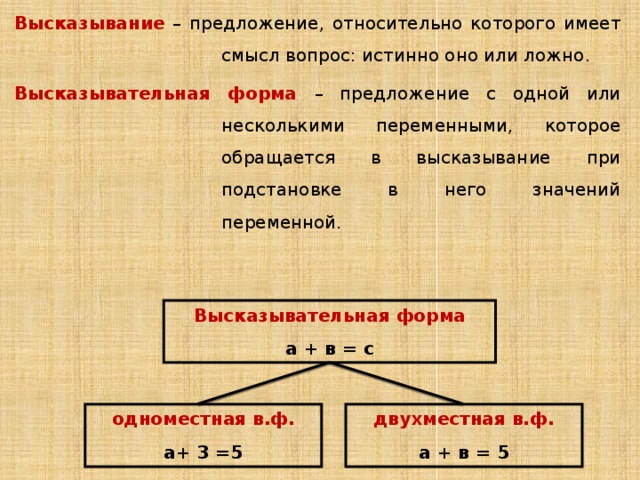
Высказывание – предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Высказывательная форма – предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него значений переменной.

Множество истинности высказывательной формы – это значения переменной, которые обращают высказывательную форму в истинное высказывание.

Пример: определить множество истинности высказывательной формы x  6, если а) x  N

Выше рассмотренные предложения – простые или элементарные предложения.

Из двух простых предложений можно составить новые предложения с помощью союзов «и», «или»…

Логическая связка – «и», «или», «если,…то», «не», «тогда и только тогда, когда».

Составные предложения – это предложения, образованные из элементарных с помощью логических связок.

Для определения логической структуры составного предложения необходимо установить :

Пример : 1) x ≥7 – это составная высказывательная форма.

Логическая структура : « А или В »

Элементарные высказывательные формы – А – «x  7»

Логическая связка – «или»

А – «треугольник равнобедренный»

В – «углы при основании равны»

Логические связки : «Если ……, то».

«Число 25 четное и делится на 5»

Элементарные высказывательные формы –

А – «25 – четное число»

В – «25 – делится на 5»

Логическая связка – « и »

Проблема : «Как определить значение истинности составных предложений?»

Составное высказывание вида «А и В» называют конъюнкцией (лат. «соединение»), обозначают А  В .

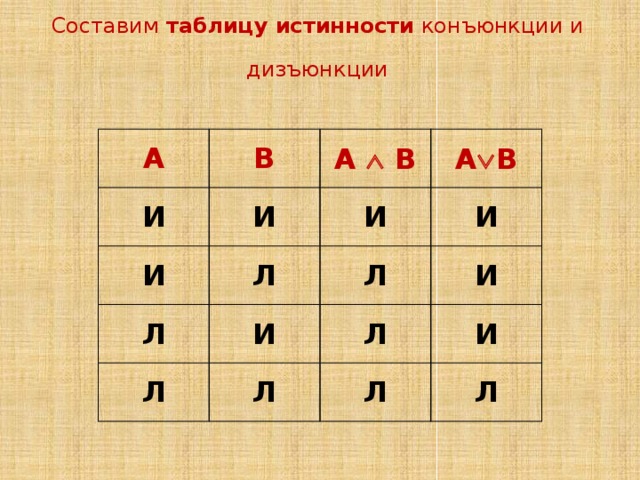
Определение. Конъюнкцией высказываний А и В называется высказывание А  В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.

Пример : А – «Л»  А  В – «Л» (по определению)

Составные высказывания вида «А или В» называют дизъюнкцией (лат. «разделение»), обозначают А  В.

Определение. Дизъюнкцией высказываний А и В называется высказывание А  В, которое истинно, когда истинно хотя бы одно из высказываний, и ложно, когда оба высказывания ложны.

Пример: «Число 25 делится на 5 или на 3».

А – «25 делится на 5»

В – «25 делится на 3»

Логическая связка – или

Логическая структура — А  В

А – «И»  – А  В «И» (по определению)

Составим таблицу истинности конъюнкции и дизъюнкции

Источник

Неверно что число 17 делится на 3 логическая связка

правила составления логических выражений

Логические операции – логическое действие.

Записывать в виде логического выражения следующее высказывание: « Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку ».

А = Петя поедет в деревню;

В = Будет хорошая погода;

С = Петя пойдет на рыбалку.

Есть два простых высказывания: А – « Число 10 – четное »; В – « Волк – травоядное животное ». Составьте из них все возможные составные высказывания и определите их истинность.

Запишите следующие высказывания в виде логических выражений.

1. Число 17 нечетное и двузначное.

3. На уроке физики ученики выполняли лабораторную работу и сообщали результаты исследований учителю.

5. Переходи улицу только на зеленый свет.

7. Если компьютер включен, то можно на нем работать.

8. Водительские права можно получить, только когда исполнится 18 лет.

9. Компьютер выполняет вычисления, если он включен.

10. Ты можешь купить в магазине продукты, если у тебя есть деньги.

12*. На уроке информатики необходимо соблюдать особые правила поведения.

13*. При замерзании воды выделяется тепло.

Составьте и запишите истинные сложные высказывания из простых с использованием логических операций.

Найдите значения логических выражений:

F 1 = (0 v 0) v ( 1 v 1 ).

F 2 = ( 1 v 1 ) v ( 1 v 0 ).

F 4 = ¬ 1 & (1 v 1) v ( ¬ 0&1).

F 5 = ( ¬ 1 v 1) & (1 v ¬ 1) & ( ¬ 1 v 0).

Составить формулы алгебры логики сложных высказываний:

1) «Неверно, что Петя едет в автобусе и читает книгу».

2) «Неверно, что Петя едет в автобусе, читает книгу или смотрит в окно».

3) «Петя не едет в автобусе, но при этом читает книгу или не смотрит в окно».

4) «Петя не едет в автобусе, не смотрит в окно – он читает книгу».

a) Запишите в виде формулы алгебры логики высказывание: «Если Алеша решит задачу, то Володя решит ее; если же Алеша не решит задачу, то об успехе Володи ничего определенного сказать нельзя – он может решить, а может не решить».

b) Запишите в виде формулы алгебры логики высказывание: «Если Ваня и Алеша проголосуют «за», то Сережа поступит так же. В случае противоположного мнения у Вани и Алеши о мнении Сережи ничего определенного сказать нельзя».

Уровень знания: выучить основные определения, знать обозначения.

Задача 1 : Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ». Запишите логические высказывания с помощью логических операций и определите их истинность.

а) Андрей старше Светы. Наташа старше Светы.

б) Один десятый класс идет на экскурсию в музей. Второй десятый класс идет в театр.

в) На полке стоят учебники. На полке стоят справочники.

Задача 2 : Для логических выражений сформулируйте составные высказывания на обычном языке:

Задача 3 : Какое логическое выражение соответствует высказыванию: « Точка X принадлежит интервалу (А; В) ».

Задача 4: Запишите на языке алгебры логики следующие высказывания:

а) Я поеду в Киев и если встречу там друзей, то мы интересно проведем время.

б) Если я поеду в Киев и встречу там друзей, то мы интересно проведем время.

в) Неверно, что если погода пасмурная, то идет дождь тогда и только тогда, когда нет ветра.

Задача 5* : приведите примеры составных высказываний из приведенных ниже школьных предметов и запишите их с помощью логических операций: биология, литература, география, математика, информатика, история, русский язык.

Источник

Высказывания и высказывательные формы

МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ

Изучая реальные процессы, математика описывает их, используя чужой естественный словесный язык, так и свой символический. Описание строится при помощи предложений. Но что бы математические предложения были достоверными, правильно отражали окружающую нас реальность, эти предложения должны быть истинными.

Но как узнать, истинное или ложное значение заключено в том или ином математическом предложении? На этот и другие вопросы, с ним связанные, мы попытаемся ответить в данном параграфе. А сейчас, коротко заметим, что каждое математическое предложение характеризуется содержанием и логической формой (структурой), причем содержание неразрывно связанно с формой, и нельзя осмысливать первое, не понимая второго. В связи с этим изучение математических предложений в главе “Элементы логики” будет в основном связанно с раскрытием логической структуры математических предложений.

Высказывания и высказывательные формы

Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:

Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:

1) число 12 – четное;

4) В числе 15 один десяток и 5 единиц;

5) От перестановки множителей произведение не изменяется;

6) Некоторые числа делятся на 3.

Видим, что предложения, используя в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предложениях 1, 4, 5 и 6 можно сказать, что они несут верную информацию, а предложение 2 – ложную. Относительно предложения х + 5 = 8 вообще нельзя сказать: истинное оно или ложное. Взгляд на предложение с позиции – истину или ложь оно нам сообщает – привел к понятию высказывания.

Определение. Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Например, предложения 1, 2, 4, 5 и 6 – высказывания, причем предложения 1, 4, 5 и 6 – истинные, а 2 – ложное.

Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z. Если высказывание А истинно, то записывают: А – «и», если же высказывание А – ложно, то пишут: А – «л».

«Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может.

Предложение х + 5 = 8 не является высказыванием, так как о нем нельзя сказать: истинно оно или ложно. Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Предложение х + 5 = 8 называется высказывательной формой. Оно порождает множество высказываний одной и той же формы.

Определение. Одноместной высказывательной формой, заданной на множестве Х, называется предложение с переменной, которое обращается в высказывание при подстановке в него значений переменной из множества Х.

Среди всех возможных значений переменной нас в первую очередь интересуют те, которые обращают высказывательную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы. Например, множеством истинности высказывательной формы х > 5, заданной на множестве действительных чисел, будет промежуток (5;∞). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.

Условимся обозначать множество истинности высказывательной формы буквой Т. Тогда, согласно определению, всегда Т⊂Х.

Предложения, которые мы рассматривали, были простыми, но можно привести примеры суждений, языковой формой которых будут сложные предложения. Например: «Если треугольник равнобедренный, то углы при основании в нем равны». Естественно возникает вопрос: как определить значение истинности таких высказываний и находить множество истинности таких высказывательных форм?

Чтобы ответить на эти вопросы, необходимо познакомиться с некоторыми логическими понятиями.

Приведем примеры составных предложений.

1) Число 28 четное и делится на 7.

Это предложение образовано из двух элементарных: “число 28 четно”, “число 28 делится на 7”с помощью логической связки “и”.

2) Число х меньше или равно 8.

Это предложение образованно из двух элементарных: “число меньше 8”, “число x меньше 8” с помощью логической связки “или”.

3) Число 14 не делится на 4.

Это составное высказывание образовано из предложения “число делится на 4” с помощью частицы “не”.

Вы, наверное, уже обратили внимание на то, что все три предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые. Не всегда, но так бывает: простое предложение по своей логической структуре может быть составным.

Кроме того, уточнение смысла используемых в математике связок обусловлено их неоднозначным толкованием в обыденной речи, что может привести к неоднозначному ответу при нахождении значения истинности составных высказываний.

Итак, значение истинности элементарного высказывания определяют, исходя из его содержания с опорой на известные знания. Чтобы определить значение истинности составного высказывания, надо знать смысл логических связок, с помощью которых оно образовано из элементарных, и уметь выявлять логическую структуру высказывания.

Для выявления логической структуры составного предложения нужно установить:

1) из каких элементарных предложений образовано данное составное предложение;

2) с помощью каких логических связок оно образованно.

Выявим, например, логическую структуру предложения “Если углы вертикальные, то они равны”. Оно состоит из двух элементарных предложений: предложения А – “углы вертикальные” и предложение В – “углы равны”. Соединены они в одно составное предложение с помощью логической связки “если …, то …”. Говорят, что данное составное предложение имеет логическую структуру (форму): “если А, то В”.

Упражнения

1. Среди следующих предложений, рассматриваемых в начальном курсе математики, укажите высказывания и определите их значение:

в) в любом прямоугольнике противоположные стороны равны;

д) среди четырехугольников есть такие, у которых все стороны равны;

е) число z – двузначное;

ж) произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174;

з) число 6 является корнем уравнения (12 – х) × 4=24.

2. Какие предложения из упражнения 1 являются высказывательными формами? Подставьте в них значение переменной так, чтобы получилось:

а) истинное высказывание;

б) ложное высказывание.

3. Можно ли считать высказывательными формами следующие записи:

Источник

Логические операции над высказываниями

Разработала: преподаватель по информатике Еникеева Оксана Юрьевна.

Урок информатики по Теме: Логические операции над высказываниями Цель: Познакомить с основными логическими операциями: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность .

Сформировать у учащихся понятие “логическая операция»;

Способствовать формированию логического мышления, интереса к изучаемому материалу.

Учащиеся должны знать:

логические операции: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность ;

таблицы истинности логических операций;

обозначение логических операций;

приоритет логических операций.

Учащиеся должны уметь:

определить порядок действий при вычислении значения логического выражения;

конструировать простые и сложные высказывания .

I. Организационный момент.

II. Изложение нового материала.

Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Логическая операция — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Рассмотрим три базовых логических операций — инверсию, конъюнкцию, дизъюнкцию и дополнительные — импликацию и эквивалентность.

Упражнение 1. Даны два простых высказывания:

В=“Щука — речная рыба”.

Составьте из них все возможные составные (сложные) высказывания и определите их истинность.

При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:

импликация и эквивалентность

Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.

Например: дана формула .

— инверсия

— конъюнкция

— дизъюнкция

— импликация

— эквивалентность.

I II . Закрепление изученного материала.

1. Какие из предложений являются высказываниями? Определите их истинность.

1. Какой длины эта лента?

2. Прослушайте сообщение.

3.Делайте утреннюю зарядку!

4. Назовите устройство ввода информации.

7. Число 11 является простым. (ИСТИНА)

9. Без труда не вытащишь и рыбку из пруда.

10. Сложите числа 2 и 5.

11. Некоторые медведи живут на севере.(ИСТИНА)

13.Чему равно расстояние от Москвы до Ленинграда.

2. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.

Число 456 трехзначное и четное.

Неверно, что Солнце движется вокруг Земли.

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.

Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.

Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться, и будут ему послушны.

3. Постройте отрицания следующих высказываний.

Сегодня выходной день.

Ваня не был готов сегодня к урокам.

Неверно, что число 3 не является делителем числа 198.

Неверно, что число 17 — простое.

4. Запишите следующие высказывания в виде логических выражений.

1.Число 17 нечетное и двузначное.

6. На уроке информатики необходимо соблюдать особые правила поведения.

10.Водительские права можно получить тогда и только тогда, когда тебе исполнится 18 лет.

12. Ты можешь купить в магазине продукты, если у тебя есть деньги.

5. По данным формам сложных высказываний запишите высказывания на русском языке.

6. Найдите значения логических выражений:

7. Даны простые высказывания: А= <1513>, В=<4=5>, C= <7

Обобщить пройденный материал, оценить работу активных учеников.

Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ». Запишите логические высказывания с помощью логических операций и определите их истинность.

1.Андрей старше Светы. Наташа старше Светы.

2.Один десятый класс идет на экскурсию в музей. Второй десятый класс идет в театр.

3.На полке стоят учебники. На полке стоят справочники.

Для логических выражений сформулируйте составные высказывания на обычном языке:

Источник