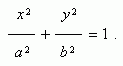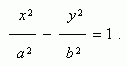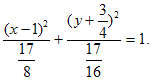какая прямая проходит через начало координат
График линейной функции, его свойства и формулы
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
4.13. Уравнения прямых на координатной плоскости
Давайте рассмотрим такие функций, графики которых имеют вид прямых. Простоты ради, мы будем иметь дело с безразмерными величинами, а значит, в качестве осей у нас будут выступать простые числовые прямые, и все наши чертежи мы будем делать на обычной координатной плоскости.
Прямая, проходящая через начало координат
Построение графика по заданной функции
Пусть переменная \(y\) пропорциональна переменной \(x\) с коэффициентом пропорциональности \(k\) :
Восстановление функции по графику
Заранее ясно, что это уравнение имеет вид
Пример нахождения уравнения прямой приведен на следующем рисунке.
Это соотношение между \(x\) и \(y\) остается справедливым в обоих рассмотренных частных случаях, однако выбор параметров не является однозначным, так как в качестве пары чисел \((x_1, y_1)\) можно взять координаты любой точки, принадлежащей прямой.
Произвольная прямая
Восстановление функции по графику
Начнем с обратной задачи. Пусть теперь на координатной плоскости дана произвольная прямая, не проходящая через начало координат. Вопрос нас будет интересовать всё тот же: графиком какой функции она является или, короче говоря, каково уравнение этой прямой?
Тогда координаты другой отмеченной точки в новой системе окажутся равны
Вообще, как мы знаем, новые («штрихованные») координаты любой точки связаны со старыми («нештрихованными») координатами соотношением
Наша прямая проходит через начало координат новой системы, поэтому мы можем сразу же выписать ее уравнение в «штрихованных» переменных:
Переходя к «нештрихованным» переменным, получаем
Что и решает поставленную задачу.
При желании, можно еще выразить функцию \(y\) от \(x\) в явном виде:
Из наших рассуждений следует, что любая прямая на координатной плоскости может быть описана уравнением вида
В совершенно общем виде уравнение прямой можно написать следующим образом:
\((x_1-x_0) (y-y_0) = (y_1-y_0) (x-x_0).\)
При этом, однако, выбор двух пар параметров \((x_0, y_0)\) и \((x_1, y_1)\) (которые, по смыслу, являются координатами двух произвольных точек, лежащих на прямой) неоднозначен.
Построение графика по заданной функции
где \(k\) и \(b\) — любые действительные числа. Как мы только что выяснили, к такому виду сводится уравнение произвольной прямой (при условии, что она не параллельна оси \(y\) ). Строго говоря, это не исключает, что при некоторых значения параметров \(k\) и \(b\) график этой функции может отличаться от прямой линии. Давайте убедимся, что этого никогда не происходит. Перепишем данное нам уравнение следующим образом:
Мы получим тогда не что иное, как уравнение пропорциональной зависимости, которое гарантировано задает прямую линию. Значит, и график неоднородной линейной функции
\(y_0 = b\) (при \(x_0 = 0\) ),
\(y_1 = k+b\,\) (при \(x_1 = 1\) ).
Проводим прямую через точки \((x_0, y_0)\) и \((x_1, y_1)\) — и задача решена. На практике, впрочем, лучше брать такие точки, которые расположены друг от друга по возможности дальше, насколько позволяет чертеж. Пример графика неоднородной линейной функции со значением параметров \(k = \frac<1><3>\) и \(b = 1\) представлен на следующем рисунке.
Конспект
Прямая линия. Уравнение прямой.
Свойства прямой в евклидовой геометрии.
Через любую точку можно провести бесконечно много прямых.
Через любые две несовпадающие точки можно провести единственную прямую.
Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются
параллельными (следует из предыдущего).
В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия
задается на плоскости уравнением первой степени (линейное уравнение).
Общее уравнение прямой.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим
уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
Уравнение прямой, проходящей через две точки.
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь 
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить 
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор 
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:


Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число 
нормирующем множителем, то получим
Формула прямой проходящей через начало координат
Давайте рассмотрим такие функций, графики которых имеют вид прямых. Простоты ради, мы будем иметь дело с безразмерными величинами, а значит, в качестве осей у нас будут выступать простые числовые прямые, и все наши чертежи мы будем делать на обычной координатной плоскости.
Прямая, проходящая через начало координат
Построение графика по заданной функции
Пусть переменная (y) пропорциональна переменной (x) с коэффициентом пропорциональности (k) :
Восстановление функции по графику
Заранее ясно, что это уравнение имеет вид
Пример нахождения уравнения прямой приведен на следующем рисунке.
Это соотношение между (x) и (y) остается справедливым в обоих рассмотренных частных случаях, однако выбор параметров не является однозначным, так как в качестве пары чисел ((x_1, y_1)) можно взять координаты любой точки, принадлежащей прямой.
Произвольная прямая
Восстановление функции по графику
Начнем с обратной задачи. Пусть теперь на координатной плоскости дана произвольная прямая, не проходящая через начало координат. Вопрос нас будет интересовать всё тот же: графиком какой функции она является или, короче говоря, каково уравнение этой прямой?
Тогда координаты другой отмеченной точки в новой системе окажутся равны
x_1 — x_0 \ y_1 — y_0end
Вообще, как мы знаем, новые («штрихованные») координаты любой точки связаны со старыми («нештрихованными») координатами соотношением
Наша прямая проходит через начало координат новой системы, поэтому мы можем сразу же выписать ее уравнение в «штрихованных» переменных:
Переходя к «нештрихованным» переменным, получаем
Что и решает поставленную задачу.
При желании, можно еще выразить функцию (y) от (x) в явном виде:
(y = k,x + b,) где (b = — k,x_0 + y_0.)
Из наших рассуждений следует, что любая прямая на координатной плоскости может быть описана уравнением вида
(x = 0 cdot (y — y_0) + x_0.)
В совершенно общем виде уравнение прямой можно написать следующим образом:
((x_1-x_0) (y-y_0) = (y_1-y_0) (x-x_0).)
При этом, однако, выбор двух пар параметров ((x_0, y_0)) и ((x_1, y_1)) (которые, по смыслу, являются координатами двух произвольных точек, лежащих на прямой) неоднозначен.
Построение графика по заданной функции
где (k) и (b) — любые действительные числа. Как мы только что выяснили, к такому виду сводится уравнение произвольной прямой (при условии, что она не параллельна оси (y) ). Строго говоря, это не исключает, что при некоторых значения параметров (k) и (b) график этой функции может отличаться от прямой линии. Давайте убедимся, что этого никогда не происходит. Перепишем данное нам уравнение следующим образом:
Мы получим тогда не что иное, как уравнение пропорциональной зависимости, которое гарантировано задает прямую линию. Значит, и график неоднородной линейной функции
(y_0 = b) (при (x_0 = 0) ),
(y_1 = k+b,) (при (x_1 = 1) ).
Проводим прямую через точки ((x_0, y_0)) и ((x_1, y_1)) — и задача решена. На практике, впрочем, лучше брать такие точки, которые расположены друг от друга по возможности дальше, насколько позволяет чертеж. Пример графика неоднородной линейной функции со значением параметров (k = frac ) и (b = 1) представлен на следующем рисунке.
Конспект
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Оно называют общим уравнением. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – проходит через начало координат
• А = 0, В ≠0, С ≠0 — параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 – параллельна оси Оу
• В = С = 0, А ≠0 – совпадает с осью Оу
• А = С = 0, В ≠0 – совпадает с осью Ох
Уравнение прямой на плоскости может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой Ах + Ву + С = 0.
Уравнение прямой, проходящей через две точки
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости, записанное выше, упрощается:
Пример 2. Найти уравнение прямой, проходящей через две точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой на плоскости Ах + Ву + С = 0 привести к виду:
Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение через вектор нормали можно ввести задание прямой через точку и направляющий вектор.
Решение.Будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Уравнение прямой в отрезках
Если в общем уравнении Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения с осью Оу.
Пример 4. Задано общее уравнение х – у + 1 = 0. Найти его в виде уравнение прямой в отрезках.
Нормальное уравнение прямой
xcosφ + ysinφ — p = 0 –
Прямая линия. Уравнение прямой.
Свойства прямой в евклидовой геометрии.
Через любую точку можно провести бесконечно много прямых.
Через любые две несовпадающие точки можно провести единственную прямую.
Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются
параллельными (следует из предыдущего).
В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия
задается на плоскости уравнением первой степени (линейное уравнение).
Общее уравнение прямой.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим
уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
Уравнение прямой, проходящей через две точки.
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь 
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить 
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор 
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:


Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число 
нормирующем множителем, то получим
xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.
5.Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Находим уравнение стороны АВ: 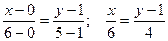
2x – 3y + 3 = 0;
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k = 



Ответ: 3x + 2y – 34 = 0.
Тема №2-4. Кривые 2 порядка: окружность, эллипс,гипербола,парабола.
Построение кривых 2 порядка. Составление уравнений кривых 2-го порядка.
Кривая второго порядка задана уравнением Ах 2 + 2Вху + Су 2 + 2Dx + 2Ey + F = 0.
Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
1) 
2) 
3) 
4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.
5) y 2 = 2px – уравнение параболы.
6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.
7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.
8) y 2 = 0 – пара совпадающих прямых.
9) (x – a) 2 + (y – b) 2 = R 2 – уравнение окружности.
Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:
Условие касания прямой y = m x + k и окружности х 2 + у 2 = R 2 :
Эллипс
Уравнение эллипса( рис.1 ) :
Гипербола
Уравнение гиперболы( рис.1 ) :
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.
Условие касания прямой y = m x + k и гиперболы х 2 / a 2 – у 2 / b 2 = 1 :
Парабола
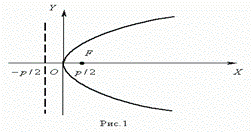
Уравнение параболы( рис.1 ) :
Здесь ось ОХ является осью симметрии параболы.
Условие касания прямой y = m x + k и параболы y 2 = 2 p x :
1.Найдите все параметры, характеризующие данные кривые второго порядка. Определите типы этих кривых, сделайте рисунки.
а) 9x² + 64y²=576
б) y²=6x
Решение.
a) 9x²+ 64y² = 576 — уравнение эллипса

a = 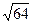

Точки А(8,0), А'(-8,0), В(0,3), В'(0,-3) — вершины эллипса
с =
Точки F( 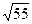
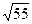
ε = с/а =( 
б) y² = 6x — уравнение параболы, симметричной относительно оси Ox,
в) Приведем данное уравнение к каноническому виду (разделив его на 144):
2. Определить вид и расположение кривой
Решение.
Дополним члены, содержащие х и у соответственно, до полных квадратов:
Следовательно, кривая, заданная исходным уравнением, представляет собой эллипс с полуосями
Центр эллипса находится в точке щ 
Решение.
В данном уравнении выделим полные квадраты, прибавляя и вычитая соответствующие числа. Получаем